定点数和浮点数的概念 浮点数二进制序列与指数表达式之间的转化

1、定点数和浮点数的概念

定点数，小数点位置固定不变，参与运算的数据其小数点固定的位于所有数字中间的某个位置，比如货币的表达，规定了使用2位整数位+2位小数表示的模式，具体数据如99.00、10.55、68.66等。定点数的缺点：由于小数点位置固定不变，定点数所表示的数的范围非常有限，不能同时表达特别大或特别小的数，所以才出现了浮点数，以此来扩充数的范围，同时浮点数也广泛应用于精度要求高的场合。简单的理解浮点数：首先浮点数小数点位置不固定，小数点是浮动的，其次浮点数提供了一种高效的数据表达方法，这种表示方法既可以表达很小的数据比如：3.14159、0.06789，也可以表达很大的数据比如：8.99910^20、510^25。

数据在计算机中的存储分为整型（char(8bit)、short(16bit)、int(32bit)、long(32bit)、long long(64bit)）和浮点型（float(32bit)、double(64bit)），计算机中不可能存储“无穷大”的数，也不能存放循环小数。（注：循环小数按照浮点数的规则存储），例如C程序中计算和输出1/3：

printf("%f",1/3.0);

得到的结果是：0.333333，只能得到6位小数，而不是理论计算的无穷位的小数。

查看我们在C语言课本上学习过的知识点：

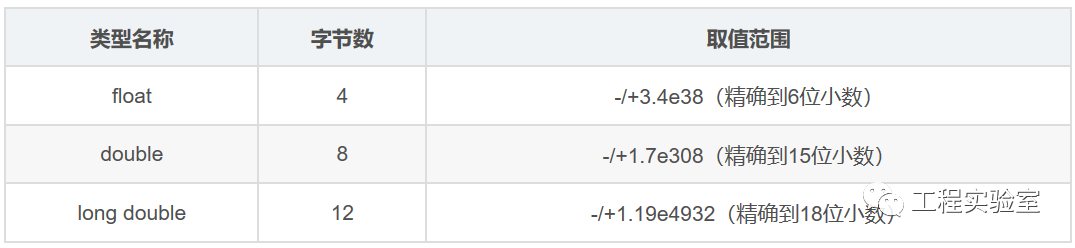
图1-1、C语言中的浮点数数据类型

2、浮点数的结构

通过图1-1，我们知道单精度浮点数(float)的取值范围为：-3.4E38 - -3.4E38，双精度浮点数(double)的取值范围是：-1.7E308 - 1.7E308，精度再高一些表示为：-1.79E308 - 1.79E308。C语言中定义相应的浮点数float和double变量以后，在编译器的帮助下即可参与相应的运算，那么浮点数的内部结构又是如何呢？下文将详细讲解。

float   a = 4.5;
double  b = 3.5e2,c;
c =  a*b;

在IEEE754标准中规定了浮点数的表达方式，浮点数的存储方式是以2为底数的表达方式。浮点数的表达中将数据表达的二进制序列分为符号位，指数位和小数位三个区域。浮点数的指数表达式如下：

x = （-1） ^s *（1.m）* 2^e;
表达32bit的浮点数时e = E-127；表达64bit的浮点数时e = E-1023，这里的127和1023称为偏移量。
公式中：
s表示符号位：正数为0，负数为1；
e表示指数位：存储指数加上偏移量，偏移量是为了表达负数而设计的；
m表示小数部分：存储小数部分的准确值或者接近的值；
注：类比科学计数法，以10为底数的表示方法中前面的系数都是小于10 的系数比如：8.bb*10^(x)；以2为底数的表示方法，前面的系数都是小于2的系数，比如：1.bb*2^(x)，前面还要符号位(-1)^s。

浮点数的二进制序列表达式中特定宽度的区域划分如下：

图2-1、不同精度浮点数特定宽度区域划分

3、浮点数二进制序列与指数表达式之间的转化

比如10进制表示的小数0.085（我们常说的小数在计算机存储系统中就是浮点数），其指数表达式为1.36*2^-4，其小数部分0.36使用了23位来表示。

图3-1、10进制小数与指数表达式的关系

在Matlab中,将浮点数转化为16进制序列

 > > a=single(0.085)
a =
  single
    0.0850
 > > num2hex(a)
ans =
3dae147b

将十六进制序列 3dae147b(H)转化为二进制序列

001111011010111000010100011110（32bit:1位符号位+8位指数位+23位小数位）

符号位：0，表示正数；

指数部分：01111011，12^0+12^1+02^2+12^3+12^4+12^5+1*2^6 = 123；

小数部分：010111000010100011110，通过表3-1来拆分每个比特位所表达的数值。

第n位	2的幂次：2^（-n）	10进制表示	求和
1	1/2-2^(-1)	0*2^(-1)=0	0
2	1/4-2^-2	1*0.25	0.25
4	1/16	1*0.0625	0.3125
5	1/32	1*0.03125	0.34375
6	1/64	1*0.015625	0.359375
11	1/2048	1*0.00048828125	......
13	1/8192	......	......
17	1/131072	......	......
18	1/262144	......	......
19	1/524288	......	......
20	1/1048576	......	......
22	1/4194304	......	......
23	1/8388608	......	0.36000001430512

表3-1、小数部分二进制序列拆分

综上：单精度浮点数0.085，使用指数表示的结果为：

(-1)^01.362^-4=1.36*2^-4，其中指数部分 e=123-127= -4，小数部分的0.36是23位二进制序列所表达的数值之和。

3.1、数据转化举例：

问题1： 十进制表达的小数0.1254，（1）、求64bit双精度浮点数的标准16进制序列，（2）、用指数形式表示。

 >>  a=double(0.1254)
a =
    0.1254
 > >  num2hex(a)
ans =
    '3fc00c435bd31c33'

双精度浮点数16进制序列为：64’h3fc00c435bd31c33

将16进制数展开后，可得二进制数格式为

0011 1111 1100 0000 0000 1100 0100 0011 0101 1011 1101 0011 0001 1100 0011 0011

符号位: bit[63] ------1位-----0---正数

指数部分： bit[62]-[52]------11位--011 1111 1100

指数部分求解十进制结果：

 > > 1*2^9+1*2^8+1*2^7+1*2^6+1*2^5+1*2^4+1*2^3+1*2^2
ans =
        1020
1020-1023=-3,浮点数的指数部分数值-减去偏移量，得到实际指数表达式中的指数为-3。

小数部分：bit[51]-[0] - 共52bit：

0000 0000 1100 0100 0011 0101 1011 1101 0011 0001 1100 0011 0011

求53bit二进制序列所表示的小数：

1*2^(-9)+1*2^(-10)+1*2^(-14)+1*2^(-19)+1*2^(-20)+1*2^(-22)+1*2^(-24)+1*2^(-25)+1*2^(-27)+1*2^(-28)+1*2^(-29)+1*2^(-30)+1*2^(-32)+1*2^(-35)+1*2^(-36)+1*2^(-40)+1*2^(-41)+1*2^(-42)+1*2^(-47)+1*2^(-48)+1*2^(-51)+1*2^(-52)
 > > 1*2^(-9)+1*2^(-10)+1*2^(-14)+1*2^(-19)+1*2^(-20)+1*2^(-22)+1*2^(-24)+1*2^(-25)+1*2^(-27)+1*2^(-28)+1*2^(-29)+1*2^(-30)+1*2^(-32)+1*2^(-35)+1*2^(-36)+1*2^(-40)+1*2^(-41)+1*2^(-42)+1*2^(-47)+1*2^(-48)+1*2^(-51)+1*2^(-52)
ans =
    0.0030

得到浮点数的指数表达式：1.0030*2^(-3)。

验证计算结果如下：

 >> 1.0030*2^(-3)
ans =
    0.1254

Matlab中浮点数转为十进制数：

 >> a='3fc00c435bd31c33'
a =
'3fc00c435bd31c33'
 > > hex2num(a)
ans =
    0.1254

问题2十进制表达的整数-5，（1）、求32bit单精度浮点数的标准16进制序列，（2）、用指数形式表示。

 > > a=single(-5)
a =
  single
    -5
 > > num2hex(a)
ans =
c0a00000

-5的浮点数表示为：

1100 0000 1010 0000000000000000000000

符号位：bit[31] --1位--1--负数

指数位：bit[30]-[23]--8位--10000001

 >> 1*2^7+1*2^0
ans =
   129
指数数值-减去偏移量，得到指数为：129-127=2

小数位：bit[22]-[0]-23位：

0100000000000000000000000，

 >> 0*2^-1+1*2^-2
ans =
    0.2500

所以-5的指数表达式为：（-1）1.252^2。

验证计算结果如下：

 >> -1*1.25*2^2
ans =
    -5

4、小数转化为定点数

在FPGA 设计开发的过程中，如果需要使用小数参与相关运算，这个时候就需要将小数转化为定点数，因为FPGA内部只能处理定点数，不能处理小数，小数转定点数的过程需要考虑符号位-整数位宽-小数位位宽。

假设将小数2.918量化为16bit的定点数，包含1bit符号位，3bit整数位，12bit小数位。16位数据能够表示的最大正数为32767（2^15-1），能够表示的最小负数为-32768。

图4-1、C语言中部分数据类型对应的取值范围

3bit整数位能够表示的最大整数是7（3'b111），12位小数位能够表示的数据的最小精度为：1/（2^12）=0.00024414，也就是说12位小数位只能表示0.00024414的整数倍，12位小数位能够表达的最大小数为：

 >> (2^12-1)*0.00024414
ans =
    0.9998

可以发现表示小数的位数越多，可以表示的小数范围越大，表示的也越精准。（小数定点量化过程中使用位宽的大小和数据精度的关系），表示小数部分0.918，需要的十进制数值为：

 >> 0.918/0.00024414
ans =
   3.7601e+03

也可以使用Matlab中的函数完成小数部分的量化。

> >  dec2bin(round(0.918*2^12),12)
ans =
111010110000
 > > bin2dec('111010110000')
ans =
        3760

所以小数2.918量化为16bit的定点数结果为：16'b0100111010110000

问题 ：将浮点数-3.125量化为8bit的定点数，包含1bit符号位，4bit整数位，3bit小数位。

方法1 ：针对负数-3.125，首先考虑其绝对值3.125，其符号位和整数部分5bit数据为：5'b00011，小数部分为0.125量化的结果为:

 >> dec2bin(round(0.125*2^3),3)
ans =
001

所以，绝对值3.125量化8bit的结果为：8'b00011001

因为是负数，需要求其补码，求补码：按位取反再加1，

得到：8'b11100111,

方法2 ：8bit能够表示的最大的数据是2^8，量化后的二进制数据中包含3位小数位，计算过程中需要修正，使用公式如下：

> > dec2bin(round(2^8-abs(-3.125)*2^3),8)
ans =
11100111

得到量化后的结果为：8'b11100111。

5、ISE中使用float-point 核

将32bit的整数1234567890转化为双精度的浮点数。

调用floating-point-IP核并配置参数；

输入的定点数据选择自定义模式；设置为32bit整数位 - 0bit小数位，表明输入数据只要整数位没有小数位。

设置转化后的浮点数为double 型；

后面的设置- 保持默认 -- 点击 Generate。

verilog代码实现如下：

module signed_2_floating(
input      wire                     sclk,
input      wire                     rst_n,
input     signed  [31:0]            data_in,
input      wire                     valid_in,
output     wire  [63:0]             floating_data,
output     wire                     valid_out


  );
reg  signed [63:0]                  floating_data_temp;
reg                                 valid_out_tmp;
// IP 核信号      
reg               data_in_tvalid;
wire              data_in_tready;
wire              result_dout_tvalid;


reg               result_dout_tready;
wire  [63:0]      result_dout_tdata;  
assign     floating_data      =      floating_data_temp;
assign      valid_out         =      valid_out_tmp ;
// data_in_tready 由IP核拉高---valid_in信号有效时--触发data_in_tvalid-开始启动计算 
always@(posedge sclk or negedge rst_n)                 
begin
  if(~rst_n)  begin
     data_in_tvalid    <=   1'b0;
  end
  else if(data_in_tready  &&  valid_in )  begin     
     data_in_tvalid   <=    1'b1;            
  end    
  else
  begin
     data_in_tvalid    <=   1'b0;
  end
end
// result_dout_tvalid - 信号由IP核输出--当检测到result_dout_tvalid 有效以后，用户端的ready信号再拉高
always@(posedge sclk or negedge rst_n)
begin
  if(~rst_n)
  begin
    result_dout_tready   <=  1'b0;
  end
  else if(result_dout_tvalid)           
  begin
    result_dout_tready   <=  1'b1;         
  end
  else
  begin
    result_dout_tready   <=  1'b0;           
  end
end
 // result_dout_tready 信号 和 result_dout_tvalid 信号都有效，开始读取数据。
always@(posedge sclk or negedge rst_n)
begin
  if(~rst_n)
  begin
    floating_data_temp    <=   64'd0;
    valid_out_tmp         <=   1'b0;    
  end
  else if(result_dout_tready && result_dout_tvalid)      
  begin
    floating_data_temp    <=    result_dout_tdata;
    valid_out_tmp         <=    1'b1;    
  end
  else
  begin
    floating_data_temp    <=    floating_data_temp;
    valid_out_tmp         <=     1'b0;        
  end
end


fixed_2_floating       floating_instance_name (
  .aclk(sclk),                                                // input aclk
  .s_axis_a_tvalid(data_in_tvalid),                           // input s_axis_a_tvalid
  .s_axis_a_tready( data_in_tready ),                         // output s_axis_a_tready
  .s_axis_a_tdata(data_in ),                                  // input [31 : 0] s_axis_a_tdata
  .m_axis_result_tvalid(result_dout_tvalid),                  // output m_axis_result_tvalid
  .m_axis_result_tready(result_dout_tready),                  // input m_axis_result_tready
  .m_axis_result_tdata(result_dout_tdata)                     // output [63 : 0] m_axis_result_tdata
);
endmodule

仿真结果展示：

验证结果：

 > > a=double(1234567890)
a =
   1.2346e+09
 > > num2hex(a)
ans =
41d26580b4800000

在Matlab中,将定点数转化为浮点数的结果和ISE中调用IP核计算的结果一致。