

傅里叶变换和系统的频域分析(1)
描述
傅里叶变换和系统的频域分析
Mother's Day
信号分解为正交函数
信号分解为正交函数的原理与矢量分解为正交矢量的概念相似。譬如,在平面上的矢量A在直角坐标系中可以分解为x方向分量和y方向分量。
例:令v,m分别是x轴和y轴的单位矢量,则矢量A可表示为C1 v +C2 m (C1,C2为常数)
因此空间矢量正交分解的概念可以推广到信号空间,在信号空间找到若干个相互正交的信号作为基本信号,使得信号空间中任一信号均可以表示成他们的线性组合。
一、正交函数集
1、正交: 如有定义在(t1,t2)区间的两个函数φ1(t)和φ2(t),若满足
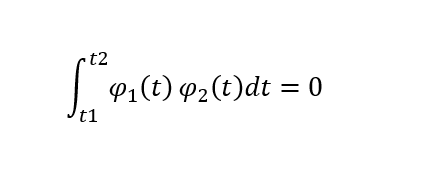
则称φ1(t)和φ2(t)在区间(t1,t2)内正交。
2、正交函数集: 如有n个函数φ1(t),φ2(t),...,φn(t)构成一个函数集,当这些函数在区间(t1,t2)内满足
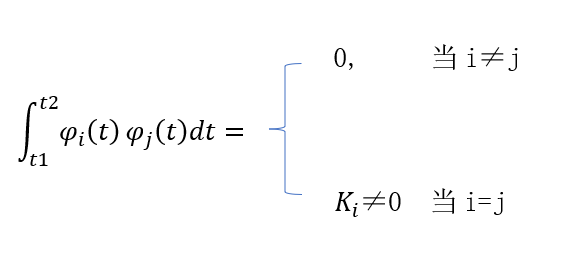
式中Ki为常数,则称此函数集为在区间(t1,t2)的正交函数集。
3、完备正交函数集:

4、三角函数集:
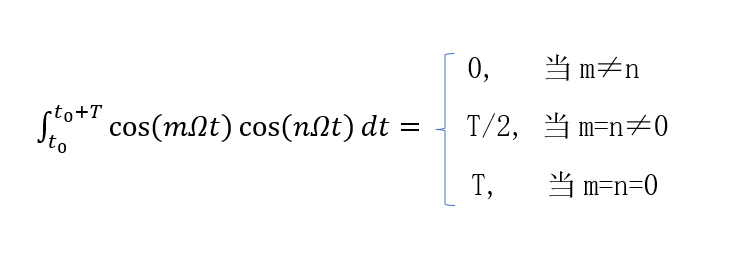
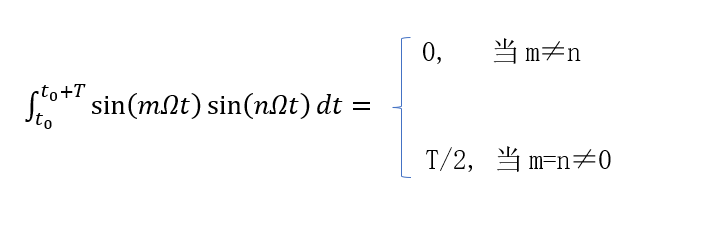
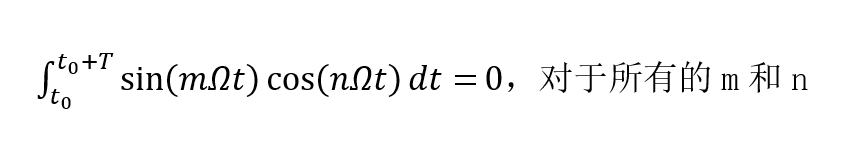
5、复函数集:
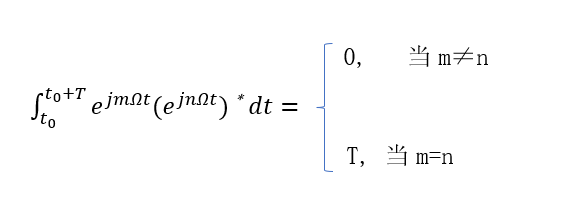
二、信号分解为正交函数



声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
傅里叶变换的应用 傅里叶变换的性质公式2024-02-02 2710
-
什么是傅里叶变换和逆变换?为什么要用傅里叶变换?2024-01-11 6203
-
傅里叶变换的定义 傅里叶变换的意义2023-11-30 3917
-
傅里叶变换的目的和意义 傅里叶变换几何意义2023-09-07 4907
-
Matlab利用离散傅里叶变换DFT进行频谱分析的步骤2023-07-20 10180
-
图像频率域分析之傅里叶变换2019-05-22 2333
-
有限长离散变换-离散傅里叶变换2011-02-23 1230
-
连续系统的频域分析2009-10-04 1158
全部0条评论

快来发表一下你的评论吧 !

