PRelu算子调优经历-函数优化策略

恩智浦MCU加油站 2023-08-24 908

恩智浦MCU加油站

174 文章 42w阅读 26粉丝

描述

上一篇小编和大家分享了在运行客户的一个模型时遇到了一个PRelu算子，在利用TFLm自带的PRelu参考实现的代码，其中PRelu竟然抛出了188ms的天文数字...因此小编开始准备PRelu算子的优化工作。

 

分析了参考实现后，发现了两个优化方向，其一是PRelu中alpha参数的特殊性所带来的内存访问优化；以及量化模型所带来的反量化问题。

本期小编就和大家一起来看下对于反量化问题的优化细节。在开始前，再来回顾一下小编所特殊定制的模型：

 

 

算子

这是一个具有5个节点的小巧的深度神经网络，输入时128*128*3，模型推理时间(采用Keil IDE，ofast优化):

 

 

算子

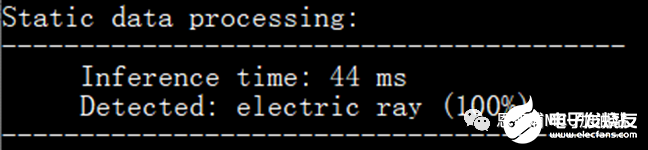
跳过PRelu算子，模型推理时间：

 

 

算子

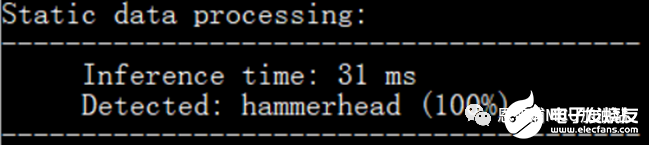
这样我们就可以得出PRelu算子的执行时间为13ms，接下来就将以此为基础进行算法优化，TFLm算法实现：

 

 

output_value = MultiplyByQuantizedMultiplier(
                  input_value, params.output_multiplier_1, params.output_shift_1);
output_value = MultiplyByQuantizedMultiplier(
                  input_value * alpha_value, params.output_multiplier_2, params.output_shift_2);

上一篇小编给大家解释了为何需要进行反量化操作以及其必要性。所谓反量化操作的本质，就是要用int8类型的中间结果来准确表达浮点结果。那么具体来说需要怎么操作呢？下面就是严谨的推公式环节，请读友们不要眨眼：

 

 

首先是整数环节，我们假设输入为input, 输出为output，参数alpha；其参数类型均为int8。而想要将其反量化为浮点数，需要为其设定对应的量化参数，分别为scale以及zero_point。这样一来，变量的浮点数表示即为：

 

v_fp=scale* (v_i8+zero_point)

为了分析简单，我们假设zero_point为0，那么上式可被简化为，当然实际计算式，只需要将输入值提前加上其zero_point再进行操作即可：

 

 

        v_fp=scale* v_i8

 

接下来我们根据输入数据的符号进行区分，当输入为正时，其输出结果为,

scale_o* output=scale_i* v_i8
output=scale_i  /  scale_0* v_i8

这样我们就可以根据输入直接获取int8类型的输出结果。

 

 

当输入为负时：

 

 

scale_o* output=(scale_a*alpha)*(scale_i* v_i8)
output=((scale_a* scale_i)/scale_0)* 〖alpha*v〗_i8)

这样也就获得了相对应的负数输入所对应的输出结果。不过，征程还没有结束，TFLm的参考实现会将这两组浮点数代表的scale参数转换为指数形式，并以mul+shift的形式保存为：正数output_multipiler_1和output_shift_1, 负数output_multipiler_2和output_shift_2。

 

 

知道了结果是如何进行反量化操作的，回过头我们看看TFLm的实现：

 

inline std::int16_t SaturatingRoundingDoublingHighMul(std::int16_t a,
                                                      std::int16_t b) {
  bool overflow = a == b && a == std::numeric_limits<std::int16_t>::min();
  std::int32_t a_32(a);
  std::int32_t b_32(b);
  std::int32_t ab_32 = a_32 * b_32;
  std::int16_t nudge = ab_32 >= 0 ? (1 << 14) : (1 - (1 << 14));
  std::int16_t ab_x2_high16 =
      static_cast<std::int16_t>((ab_32 + nudge) / (1 << 15));
  return overflow ? std::numeric_limits<std::int16_t>::max() : ab_x2_high16;
}
inline int32_t MultiplyByQuantizedMultiplier(int32_t x,
                                             int32_t quantized_multiplier,
                                             int shift) {
  using gemmlowp::RoundingDivideByPOT;
  using gemmlowp::SaturatingRoundingDoublingHighMul;
  int left_shift = shift > 0 ? shift : 0;
  int right_shift = shift > 0 ? 0 : -shift;
  return RoundingDivideByPOT(SaturatingRoundingDoublingHighMul(
                                 x * (1 << left_shift), quantized_multiplier),
                             right_shift);
}

首先arm的cmsis-nn库是兼容这种量化方式的，那么他也一定有一个这样的实现，功夫不负有心人，这个函数叫做arm_nn_requantize，直接替换MultiplyByQuantizedMultiplier函数让我们先看一下速度：

算子

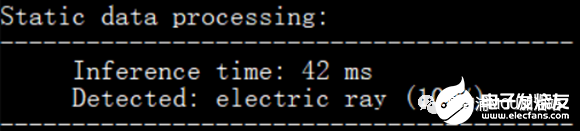
嗯，不错，有效果，44ms->42ms，相当于PRelu算子执行速度从13ms->11ms; 还可以，无痛涨点。翻看arm_nn_requantize函数，其中也不乏一些手撕浮点数的神秘操作。考虑到我们的RT1170本身兼备一个FPU单元，为啥不直接用浮点数计算呢？这次我们不对scale参数进行指数化转换，而是直接将其作为浮点数参与运算，公式就是上面我们推导的：

 

 

 // init the float mul, shift
  float real_multiplier_1 = (input->params.scale) / (output->params.scale);
  float real_multiplier_2 = (input->params.scale) * (alpha->params.scale) / (output->params.scale);

计算方式重新定义为：

output_value = MultiplyByQuantizedMultiplierFP32(
                input_value, multiplier_pos);
static inline int32_t MultiplyByQuantizedMultiplierFP32(int32_t x, float mul){
  return roundf(x * mul);

是不是看着非常清爽？让我们看下时间：

 

 

 

算子

 

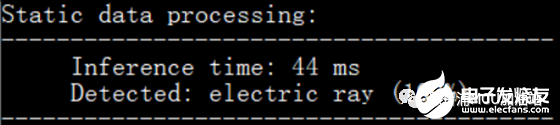
额。。。有点尴尬，竟然没有长点，而且和TFLm的原始实现速度一样。小编才提到的内存优化不是还没有上？浮点运算这边还有小插曲，让我们继续前行：

 

 

首先让我们先看下浮点操作再如何进行优化，由于我们的代码由于采用了Ofast优化策略，因此代码的可阅读性变得很差。为了进行代码优化，小编需要特殊编写一组浮点运算代码以供优化参考，因为我们最终实现的是一个int32数据与浮点数相乘：

static inline int32_t MultiplyByQuantizedMultiplierFP32(int32_t x, float mul){
  return roundf(x * mul);
}

编写代码如下：

 int32_t v1 = (float)SysTick->VAL;
    float v2 = SysTick->VAL * 0.0001f;
    int32_t v3 = (v1 * v2);
    PRINTF("%d", v3);

其所生成的汇编代码为：

int32_t v1 = (float)SysTick->VAL;
     800040DC   LDR            R2, [R0]
     800040DE   STRD           R2, R1, [SP]
     800040E2   VLDR           D0, [SP]
     800040E8   VSUB.F64       D0, D0, D1
     800040F0   VCVT.F32.F64   S0, D0
     800040F8   VCVT.S32.F32   S0, S0
     800040FE   VMOV           R0, S0
    float v2 = SysTick->VAL * 0.0001f;
     800040E6   LDR            R0, [R0]
     800040EC   STRD           R0, R1, [SP, #16]
     800040F4   VLDR           D2, [SP, #16]
     80004102   VSUB.F64       D0, D2, D1
     80004106   VLDR           D2, =0x4330000080000000
     80004110   VCVT.F32.F64   S0, D0
     80004122   VMUL.F32       S0, S0, S4
    int32_t v3 = (v1 * v2);
     800040FC   STR            R1, [SP, #12]
     8000410A   EOR            R0, R0, #0x80000000
     8000410E   STR            R0, [SP, #8]
     80004116   VLDR           D1, [SP, #8]
     8000411A   VSUB.F64       D1, D1, D2
     8000411E   VLDR           S4, =0x38D1B717            
     80004126   VCVT.F32.F64   S2, D1
     8000412A   VMUL.F32       S0, S2, S0

 

 

到这里，小伙伴们可能已经看到了端倪，小编也特意为大家标红了几条汇编代码。那小编就先抛出疑问：我们明明定义的浮点型, 咋还用上double类型了呢？相同的代码用GCC编译会是什么样的呢？

 

int32_t v1 = (float)SysTick->VAL;
300030f2:   mov.w   r3, #3758153728 ; 0xe000e000
300030f6:   vldr    s15, [r3, #24]
71            float v2 = SysTick->VAL * 0.0001f;
300030fa:   vldr    s14, [r3, #24]
300030fe:   vcvt.f32.u32    s14, s14
30003102:   vldr    s13, [pc, #92]  ; 0x30003160 +148>
30003106:   vmul.f32        s14, s14, s13
72            int32_t v3 = __builtin_roundf(v1 * v2);
3000310a:   vcvt.f32.s32    s15, s15
3000310e:   vmul.f32        s15, s15, s14
30003112:   vrinta.f32      s15, s15

看似正常，没有使用double类型寄存器；那问题出在哪呢？难道Keil对于浮点数的支持不太行？翻阅了一万件资料之后，小编在编译时使用一个叫做-ffp-mode = full的参数，这个参数的意思是：

 

算子

 

同时还有两个参数，是-fp-mode=fast和-fp-mode=std，简单来讲就是full会保证转换精度，因此会出现使用double类型的情况。而fast可能会丢失一点精度，而std介于两者之间。那么我们定义-fp-mode=std试试？

 

 

算子

代码如下：

int32_t v1 = (float)SysTick->VAL;
     800040D4   VLDR           S0, [R0]
     800040E2   VCVT.F32.U32   S0, S0
    float v2 = SysTick->VAL * 0.0001f;
     800040D8   VLDR           S2, [R0]
     800040DC   VCVT.F32.U32   S2, S2
     800040E6   VMUL.F32       S2, S2, S4
    int32_t v3 = (v1 * v2);
     800040EA   VRINTZ.F32     S0, S0
     800040EE   VMUL.F32       S0, S2, S0

嗯，优雅，就是这么简单。指令条数减少了很多啊，让我们再来看看时间：

 

算子

 

这样一来就和arm提供的方式一致了，相比实现就清爽了很多。

 

 

接下来小编还有一个杀手锏，内存优化，不过此处的内存优化是有个前提，我们知道PRelu的alpha参数是按通道的，这里要做个特殊的假设，假设输入维度为 h w c，而且alpha参数是按h w共享的，即只有最后一维参数，维度为11 c：

 

 

if((alpha_shape.Dims(0) == 1) && (alpha_shape.Dims(1) == 1))

这样我们就可以按c通道进行展开，并进行顺序访问；

 

 

其次，输入数据为int8类型，原始实现方式中每次只取一个数据进行计算：

 

const int32_t input_value =
              params.input_offset + input_data[input_index];

这样编译器会将起编译为LDRB指令，即每次只获取一个字节的数据。对此进行优化，每次读取4个字节的数据，这样可以编译为LDR指令，并放置于寄存器中，减少访存次数：

uint32_t steps = alpha_shape.Dims(2);
uint32_t total_size = input_shape.Dims(0) * input_shape.Dims(1) * input_shape.Dims(2) * input_shape.Dims(3);
for(int value_index=0;value_index    T *alpha = (T *)alpha_data;
    // each 4, calc the time_tick
    uint32_t inner_loop = steps >> 2;
    int8_t *input_data_ptr = (int8_t*)input_data + value_index;
    int8_t *output_data_ptr = (int8_t*)output_data + value_index;
    while(inner_loop --){
       int32_t input_data_32 = *((int32_t*)(input_data_ptr));
       input_data_ptr += 4;
       uint32_t count = 4;
          while(count--){
              int8_t input_data_8 = input_data_32 & 0xFF;
              input_data_32 >>= 8;
       。。。。

;value_index+=steps){>

这样一来，就可以顺序取数据，并且每次读取4个字节，看下时间：

 

算子

 

Nice!~

PRelu的时间变为37ms – 31ms = 6ms。经过两步优化，将PRelu的执行时间降低了7ms。用客户的模型测试一下，PRelu算子运行时间从之前的188ms降低到了51ms。Perfect!

不过，小编精益求精，还有一些微小的优化空间，后续将会进一步优化。

欢迎朋友们持续关注~


打开APP阅读更多精彩内容
声明：本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人，不代表电子发烧友网立场。文章及其配图仅供工程师学习之用，如有内容侵权或者其他违规问题，请联系本站处理。 举报投诉

全部0条评论

快来发表一下你的评论吧 !

下载APP
|投诉反馈|电子发烧友网
© 2021 elecfans.com
湘ICP备2023018690号
×
20
完善资料，
赚取积分