有限增益带宽积补偿及对active-RC滤波器Q值的影响

　　文章从数学上分析了运算放大器的有限增益带宽积对active-RC滤波器Q值的影响，得出了滤波器Q值升高的结论，并且研究了滤波器Q值升高的补偿方法。我们对5阶低通滤波器的Biquad引入补偿电容Cm的前后进行仿真对比，发现补偿电容Cm会使滤波器的Q值降低，并抵消由于运放有限增益带宽积带来的影响。

　　 引言

　　active-RC滤波器是基于运放的负反馈应用，它的线性度很高，所以active-RC滤波器最适合做信道选择滤波器。运放是active-RC滤波器中的关键模块，滤波器的带宽越宽，Q值越高，对运放的增益带宽积(GBW)的要求也就越高，滤波器的性能通常受限于运放的GBW。运放的有限GBW对active-RC滤波器的最主要影响是使其Q值升高，关于这方面的经验性结论多，具体的数学分析却很少。本文从数学上来分析运放的有限GBW对滤波器Q值的影响，推导出具体公式，并且研究其补偿方法。

　　1 运放的有限GBW对active-RC滤波器Q值的影响

　　

 

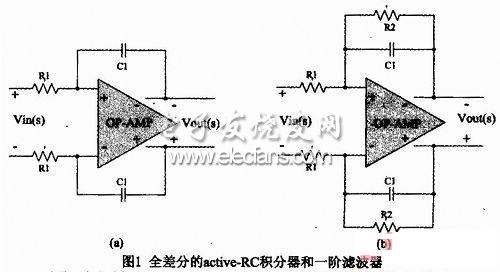
　　图1(a)是active-RC积分器，它是滤波器中基本的单元模块，其理想传输函数为式(1)：

　　

 

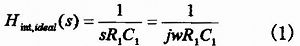
　　积分器的理想品质因子Qint,ideal→∞，相位φint,ideal=-π/2。 实际上运放的有限GBW影响其传输函数，我们把运放近似为一个单极点系统，其传输函数为式(2)：

　　

 

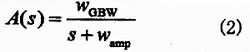
　　Wamp是运放的主极点，WGBW是运放的增益带宽积。在我们感兴趣的频率范围内，运放的传输函数可以简化为式(3)：

　　

 

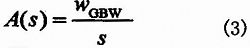
　　考虑到运放的有限GBW，通常WGBW>>1/R1C1，积分器的实际传输函数为式(4)：

　　

 

　　图1(b)是一阶Active-RC滤波器，它同样是滤波器中基本的单元模块，其理想传输函数为式(7)：

　　

 

　　从式(12)可以得出，一阶滤波器的实际Q值会由于运放的有限GBW而升高。

　　

 

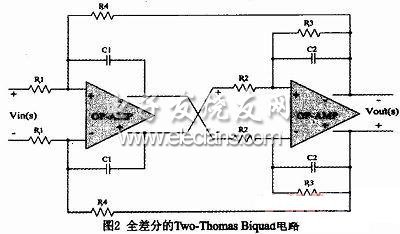
　　在分析了active-RC滤波器中的一阶单元模块的基础上，我们接下来分析滤波器的二阶单元模块Biquad，Biquad是滤波器中最基本的二阶模块。图2是Two-Thomas Biquad电路，我们采用的Two-Thomas Biquad是一种非常灵活可调的Biquad电路结构，它的灵敏度低，其理想传输函数为式(13)：

 

　　从式(17)可以得出，Biquad的Q值同样会因为运放的有限GBW而升高。以上是针对一阶系统和二阶系统推导的，对于级联的高阶系统完全可以依次类推。根据式(12)和(17)，为了使运放的有限GBW对滤波器Q值影响比较小，则WGBW必须远远大于Q*wp。

　　

 

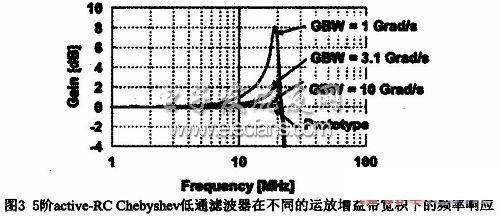
　　为了验证前面的理论分析，我们对一个5阶active-RC低通滤波器进行仿真，在不同的运放GBW下的频率响应如图3所示。这个滤波器的LCR原型是5阶Chebyshev I型低通滤波器，带宽是19.7MHz，带内纹波0.1dB。从图3可以看出，运放的GBW越宽，active-RC滤波器的实际频率响应与理想的LCR原型滤波器越接近;运放的GBW越窄，active-RC滤波器的实际Q值越高，越偏离滤波器的理想特性。同时可以看出，要使滤波器的实际频率响应接近LCR原型的频率响应，所需的运放GBW很大，这在具体电路设计上难以实现，并且消耗的电流也太大。

　　2 针对active-RC滤波器Q值升高的补偿方法

　　从前面的分析得出，如果要使滤波器的频率响应接近LCR原型的话，所需运放的GBW很大，甚至不现实。所以我们就必须研究其补偿方法，让滤波器的Q值降低，与理想的LCR原型接近。对比式(15)和式(16)，可以看出由于运放的有限GBW使Two-Thomas Biquad产生了额外的相位-2wp/WGBW，这个额外的相位为式(18)：

　　

 

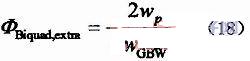
　　从式(18)看出，这是一个相位滞后，因此我们必须引入一个超前的相位来补偿。在图4中引入电容Cm对active-RC滤波器的Biquad进行相位超前补偿，其超前的相位为式(19)：

　　

 

　　

 

　　

 

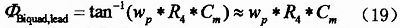
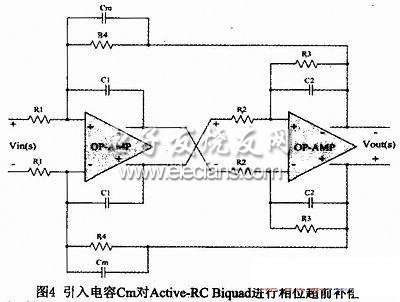
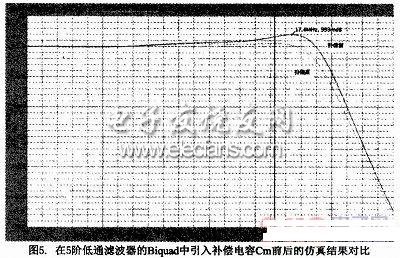
　　对比式(18)和式(19)，如果选择l/R4*Cm=WGBW/2，则由运放的有限GBW引入的滞后相位和补偿电容Cm引入的超前相位可以相互抵消，避免滤波器Q值升高，减小对运放GBW和功耗的要求。图5是在相同的运放GBW的情况下，在一个5阶低通滤波器的Biquad引入补偿电容Cm前后的仿真对比，从图中可以看出，补偿电容Cm使滤波器的Q值降低，抵消由于运放有限GBW带来的影响。在实际的电路设计中由于要保证滤波器具有一定的线性度和稳定性，运放的带宽不能太小，通常选择运放的GBW为滤波器Q*wp的10倍左右。

　　4 结论

　　在相同的运放GBW的情况下，对5阶低通滤波器的Biquad引入补偿电容Cm的前后进行仿真对比，发现补偿电容Cm会使滤波器的Q值降低，并抵消由于运放有限GBW带来的影响。