

一文详解有源高通滤波电路
电子说
描述
高通滤波器将允许高于截止频率的频率,并衰减低于截止频率的频率。在某些情况下,此滤波器也称为“低切”滤波器或“基切”滤波器。衰减量或通带范围将取决于滤波器的设计参数。
有源滤波器的通带增益大于单位增益。有源高通滤波器的工作原理与无源高通滤波器相同,但主要区别在于有源高通滤波器使用运算放大器,它提供输出信号的放大和控制增益。
高通滤波器的理想特性如下所示。
我们知道,高通滤波器会将频率从截止频率点传递到“无穷大”频率,这在实际考虑中是不存在的。除了该有源高通滤波器中的无源高通滤波器外,最大频率响应还受到运算放大器开环特性的限制。
有源高通滤波电路
通过将无源RC高通滤波器电路连接到运算放大器的反相或同相端子,我们可以得到一阶有源高通滤波器。连接到单位增益运算放大器同相端的无源RC高通滤波电路如下图所示。

ThegainAmax=1andcutofffrequencyfc=1/2πRC
具有高电压增益的有源高通滤波器
其操作与无源高通滤波器相同,但输入信号由输出端的放大器放大。放大量取决于放大器的增益。
通带增益的幅度等于1+(R3/R2).其中R3是反馈电阻,单位为Ω(欧姆)和R2是输入电阻。带放大的有源高通滤波器电路如下

高通滤波器的电压增益
电压增益Av=A.max(f/fc)/√{1+(f/fc)²}
其中f=工作频率
fc=截止频率
A.max=滤波器的通带增益=1+(R3/R2)
在低频时,即当工作频率小于截止频率时,电压增益小于通带增益A.max.在高频下,即当工作频率大于截止频率时,滤波器的电压增益等于通带增益。
如果工作频率等于截止频率,则滤波器的电压增益等于0.707A.max.
电压增益(分贝)
电压增益的大小通常以分贝(dB)为单位:
Av(dB)=20对数10(Vout/Vin)
-3dB=20log10(0.707*Vout/Vin)
分隔通带和阻带的截止频率可以使用以下公式
fC=1/(2πRC)
有源高通滤波器的相移等于无源滤波器的相移。它等于截止频率fC处的+45°,该相移值等于
Ø=tan-1(1/2πfcRC)
有源高通滤波器的频率响应
相对于放大器开环增益的频率响应曲线如下所示。

在有源高通滤波器的频率响应中,最大通带频率受带宽或运算放大器开环特性的限制。由于此限制,有源高通滤波器响应将类似于宽带滤波器响应。
通过使用这种基于运算放大器的有源高通滤波器,我们可以通过使用低容差电阻和电容器来实现高精度。
采用反相运算放大器的高通有源滤波器
我们知道,有源高通滤波器可以通过使用运算放大器的反相端或同相端来设计。到目前为止,我们看到了同相有源高通滤波器的高通滤波器电路和响应曲线。现在让我们看看使用反相运算放大器的有源高通滤波器。

拉普拉斯形式的增益推导
让我们考虑如下所示的反相放大器。

输入阻抗Z1=1/sC1
其中s=拉普拉斯变量
C1=电容
电路中流动的电流为I1、I2和Iin,
其中I1=I2且Iin=0
Vin/Z1=-Vout/R1
Vout/Vin=–R1/Z1
Vout/Vin=–R1/(1/sC1)
Vout/Vin=-sR1C1=Gain
有源高通滤波器示例
我们将截止频率值视为10KHz,通带增益A.max为1.5,电容值为0.02μF
截止频率的公式为fC=1/(2πRC)
通过重新排列这个方程,我们有R=1/(2πfC)
R=1/(2π100000.02*10-6)=795.77Ω
滤波器的通带增益为A.max=1+(R3/R2)=1.5
R3=0.5R2
如果我们将R2值视为10KΩ,则R3=5kΩ
我们可以按如下方式计算滤波器的增益
高通滤波器的电压增益|Vout/Vin|=A.max*(f/fc)/√[1+(f/fc)²]
通过使用这个方程,让我们将频率范围的响应制成表格,以绘制滤波器的响应曲线。这些响应假定为10Hz至100KHz。

波特图
为了分析电路频率响应,使用此波特图。它只不过是线性、时变与频率的传递函数的曲线。这是用对数频率轴绘制的。它主要由两个地块组成;一个是幅度图,另一个是相位图。
幅度图将表示频率响应的幅度,即增益,相位图用于表示频移的响应。
根据上表值的频率响应波特图如下所示:

根据计算的值,在频率10Hz时,以dB为单位获得的滤波器增益为-56.48。如果我们将频率值增加到100Hz,则获得的增益为-36.48dB,在频率为500Hz时,滤波器的增益为-22.51dB。
在频率1000Hz时,以dB为单位的增益为-16.52。我们可以说,如果频率增加,滤波器的增益将以20dB/十倍频程的速率增加。
截止频率为10KHz时,滤波器的增益增加,但在截止频率之后,增益达到最大值且恒定。
二阶高通滤波器
二阶有源滤波器频率响应与二阶有源低通滤波器响应完全相反,因为该滤波器会将电压衰减到截止频率以下。二阶滤波器的传递函数如下所述Vout(s)/Vin(s)=-Ks²/s²+(ω0/Q)s+ω0²
WhereK=R1/R2andω0=1/CR
这是二阶高通滤波器的一般形式。
二阶有源高通滤波器电路
二阶有源滤波器的设计过程与一阶滤波器的设计过程相同,因为唯一的变化是滚降。如果一阶有源高通滤波器的滚降为20dB/十倍频程,则二阶滤波器的滚降为40dB/十倍频程。
它表示一阶滤波器值的两倍。二阶滤波器的电路如下所示。
滤波器的增益为1+R1/R2,截止频率的公式为fc=1/2π√R3R4C1C2
二阶有源高通滤波器示例
我们设计一个截止频率为4KHz的滤波器,阻带中的延迟率为40dB/十倍频程。由于阻带中的延迟率为40dB/十倍频程,我们可以清楚地说该滤波器是二阶滤波器。
我们考虑电容值为C1=C2=C=0.02μF
截止频率的公式为R=1/2πfC
通过重新排列这个方程,我们得到R=1⁄2πfC
将截止频率值代入4KHz,将电容值代入0.02μF
R=1.989KΩ=2KΩ。
设滤波器增益为1+R1/R2=2
R1/R2=1
R1=R2
因此我们可以取R1=R2=10KΩ
因此,得到的滤波器如下所示。

高阶高通滤波器
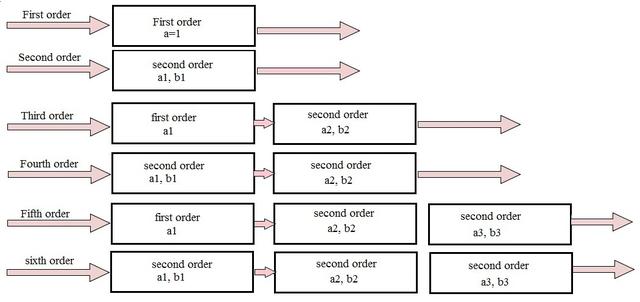
通过级联一阶滤波器和二阶滤波器,我们可以得到三阶滤波器。当我们级联两个二阶滤波器时,我们可以得到四阶滤波器。像这样,在一阶和二阶滤波器的帮助下,我们得到了高阶滤波器。
随着滤波器阶数的增加,实际阻带与理论阻带之差增大。但是高阶滤波器的总增益是相等的,因为我们已经看到决定频率响应值的电阻和电容是相同的。
此级联顺序如下所示。
有源高通滤波器的应用
- 这些用于扬声器中以减少低电平噪音。
- 消除音频应用中的隆隆声失真,因此这些也称为高音增强滤波器。
- 这些用于音频放大器中以放大更高频率的信号。
- 这些也用于均衡器。
-
应用于有源高通滤波电路的高速运放2024-12-27 772
-
有源滤波电路讲解2023-04-13 2867
-
一文详解分立元件门电路2023-03-27 4578
-
二阶有源带通滤波器原理详解2022-11-21 5701
-
二阶有源高通滤波器原理详解2022-11-18 5132
-
一阶有源滤波器原理详解2022-11-14 3749
-
一些经典的有源滤波电路2021-06-07 1082
-
高阶有源滤波电路相关知识的解析2017-11-22 1665
-
高Q值有源滤波器2012-12-25 2815
-
什么是有源滤波电路?什么是无源滤波电路?2011-11-11 8531
-
有源滤波电路设计总结2011-11-10 7783
-
有源滤波器的主电路2009-07-18 2511
-
高通有源滤波器电路图2009-03-30 1971
-
有源滤波电路2006-04-16 4438
全部0条评论

快来发表一下你的评论吧 !

