电阻网络中的电位差是如何定义的？

电位差定义

考虑在均匀电场中将电荷从A移动到B的任务。让这种运动与电场相对立。一些功将由外力对该电荷完成，并且该功会将势能更改为更高的值。完成的功量等于势能的变化。势能的这种变化将导致两点A和B之间的电位差。这种电位差称为电位差，以伏特 （V） 为单位进行测量。

电位差用∆V表示，定义为两点之间的电位或电压差。
如果 VA 是 A 处的电位，VB 是 B 处的电位，那么从电位差的定义来看，

∆VBA = VB – VA

例如，考虑以下电阻R1。

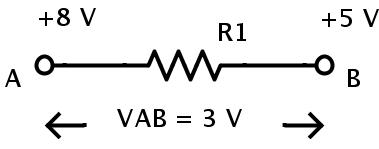
施加在电阻一端（A点）的电位为8 V，电阻另一端（B点）的电位为5 V。

两点 A 和 B 之间的电位差为

VAB = 8 – 5 = 3 V。

这也称为电阻两端的电位。

电流以电荷的形式在电路中流动，而电位不会流动或移动。两点之间应用电位差。

两点之间的电位差单位是伏特。伏特定义为 1 欧姆 （Ω） 电阻器上的电位降，其中 1 安培电流流过它。

因此

1 伏 = 1 安培×1 欧姆

V = I × R

根据欧姆定律，线性电路中流动的电流与电路上的电位差成正比。因此，如果施加在电路上的电位差更大，则电路中流动的电流更大。

例如，如果1 Ω电阻的一侧处于8 V电位，另一侧处于2 V，则电阻两端的电位差为5 V。流入电阻器的电流为

I = V/R= 5V/1 Ω = 5 安培。

现在，对于相同的1 Ω电阻，如果一端施加的电位从8 V提高到12 V，另一端的电位从2 V提高到4 V。然后，电阻两端的电位差现在为8 V。在这种情况入电阻器的电流为 8 安培。

I = V/R= 8V/1 Ω = 8 安培。

通常在电路中，较低的电位是大地或接地。该值通常被认为是0 V，因此电位差等于施加的电压。接地被认为是电路中的公共点。这种将接地或接地作为电路中公共点的参考有助于轻松理解电路。电位差也称为电压。

串联的电压相加，给出电路中的总电压。这可以在串联连接的电阻器中观察到。如果 V1、V2 和 V3 串联，则总电压 VT 由下式给出

VT= V1 + V2 +V3。

如果元件并联，则它们两端的电压相等。这可以在并联教程中的电阻器中观察到。

VT= V1 = V2 = V3。

电位差示例

• 如果转移 1500 焦耳的势能以在电池的端子之间移动 125 库仑的电荷，则电位差为

∆E = 1500 J

Q = 125 C

电位差 V = ∆E / C

V = 1500 / 125 = 12 焦耳 / 库仑 = 12 V

2. 考虑电阻为 10 Ω的电阻。让电阻的一端连接到15 V的电位。让电阻的另一端连接到5 V电位。流过电阻的电流可以计算如下。

电阻器的两个端子分别处于两个不同的电位，即 15 V 和 5 V。设两个端子为 A 和 B。因此，A 处的电压为 VA = 15 V，B 处的电压为 VB = 5 V。然后，A和B之间的电位差是电阻两端的电压。

VAB = VA – VB = 15 – 5 = 10 V。

然后可以使用欧姆定律计算流过电阻器的电流

I = VAB / R = 10 / 10 = 1 安培。

分压器电路

串联电阻用于产生分压器电路。分压器是一种线性电路，其输出电压是输入电压的一小部分。

下面显示了带有2个电阻的简单分压器电路。

串联连接中每个电阻两端的电位取决于电阻值。分压器的原理是产生一个是输入电压的一小部分的电压。

以下电路用于显示多个输出电压的分压器原理。

此处电阻R1、R2、R3和R4串联。每个电阻两端的输出电压以公共点P为基准。设串联电阻的等效电阻为RT。然后 RT= R1 + R2 + R3 + R4。

让每个电阻两端的电位差为 VR1， VR2， VR3和 VR4分别用于 R1、R2、R3 和 R4。然后，上述电路可以产生4种不同的电压，这些电压是电源电压V的分数。

分压器公式

典型分压器电路中的输出电压值计算如下。

此处的 Vin 是电源电压。I是电路中流过两个电阻的电流。

设VR1是电阻R1两端的压降，VR2是电阻R2两端的压降。然后，这些单个压降的总和等于电路两端的总电压，即电源电压Vin。

Vin = VR1 + VR2 – – – 1

每个电阻上各个压降的公式可以根据欧姆定律计算得出。

VR1 = I × R1 – – – 2

VR2 = I × R2 – – – 3

但电阻R2两端的电压为VOUT。

因此 VOUT = I × R2 – – – 4

因此，从等式 1、2 和 3

Vin = I × R1 + I × R2 = I × （R1 + R2） – – – 5

但是电流I在输出电压方面的值可以使用公式4写如下。

I = VOUT / R2 – – – 6

使用等式 5 和 6

VOUT = 电压× （R¬2 / R1 + R2）

因此，VOUT = VIN × R2/（R1+R2）

对于具有多个输出的分压器电路，可以使用以下公式计算输出电压。

VX = V × （RX / REQ）

其中 VX 是要找到的电压。

RX是输出电压上的总电阻。

RX 的可能值为

R1 介于 P 和 P1 之间

R 1 + R2 介于 P 和 P2 之间

R1 + R2 + R3 在 P 和 P3 之间

R1 + R2 + R3 + R4 在 P 和 P4 之间。

R情 商是串联连接中电阻的等效电阻。

R情 商= R1 + R2 + R3 + R4

V是电源电压。

因此，可能的输出电压为

V1 = V × R1 / R情 商

V2 = V ×（R1 + R2） / R情 商

V3 = V × （R1 + R2 + R3） / R情 商

V4 = V × （R1 + R2 + R3 + R4） / R情 商= V

分压器示例

考虑以下分压器电路。

它由三个串联的电阻组成，以产生两个输出电压。电源电压为 240 V。

电阻值为 R1 = 10 Ω、R2 = 20 Ω和 R3 = 30 Ω。

因此电路的等效电阻为

R情 商= R1 + R2 + R3 = 10 + 20 + 30 = 60 Ω。

现在，两种可能的输出电压可以计算如下：

V输出1= V × （R2 + R3） / REQ

V输出1= 240 × （20 + 30） / 60

V输出1= 200 V。

V输出2= V× R3 / REQ

V输出2= 240 × 30 / 60

V输出2= 120 V.

电路中的电流为

I = V / R情 商= 240 / 60 = 4 安培。

因此，每个电阻器上的各个压降可以计算如下：

VR1= I × R1 = 4 × 10 = 40 V。

VR2= I × R2 = 4 × 20 = 80 V。

VR3= I × R3 = 4 ×30 = 120 V。

分压器电路的应用

串联的电阻器将形成分压器电路。分压器原理是电位计结构的基础，电位计充当简单的电压调节器。

分压器电路用于传感电路。分压器电路形式最常用的传感器是热敏电阻和光相关电阻器。