

十分钟读懂旋转编码(RoPE)
描述
旋转位置编码(Rotary Position Embedding,RoPE)是论文 Roformer: Enhanced Transformer With Rotray Position Embedding 提出的一种能够将相对位置信息依赖集成到 self-attention 中并提升 transformer 架构性能的位置编码方式。而目前很火的 LLaMA、GLM 模型也是采用该位置编码方式。
和相对位置编码相比,RoPE 具有更好的外推性,目前是大模型相对位置编码中应用最广的方式之一。
备注:什么是大模型外推性?
外推性是指大模型在训练时和预测时的输入长度不一致,导致模型的泛化能力下降的问题。例如,如果一个模型在训练时只使用了 512 个 token 的文本,那么在预测时如果输入超过 512 个 token,模型可能无法正确处理。这就限制了大模型在处理长文本或多轮对话等任务时的效果。
旋转编码RoPE
1.1 基本概念
在介绍 RoPE 之前,先给出一些符号定义,以及基本背景。
首先定义一个长度为 的输入序列为:
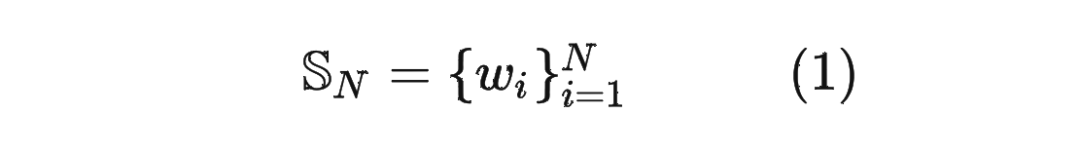
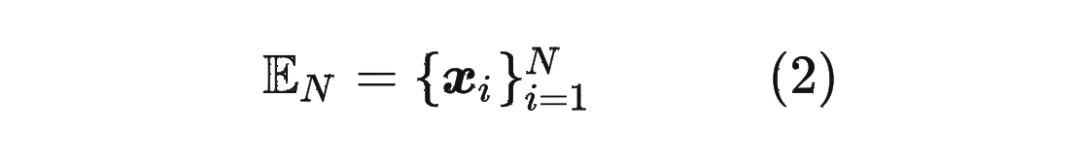
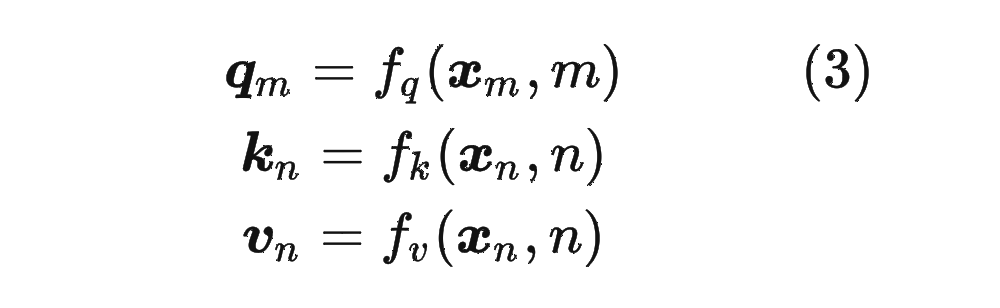
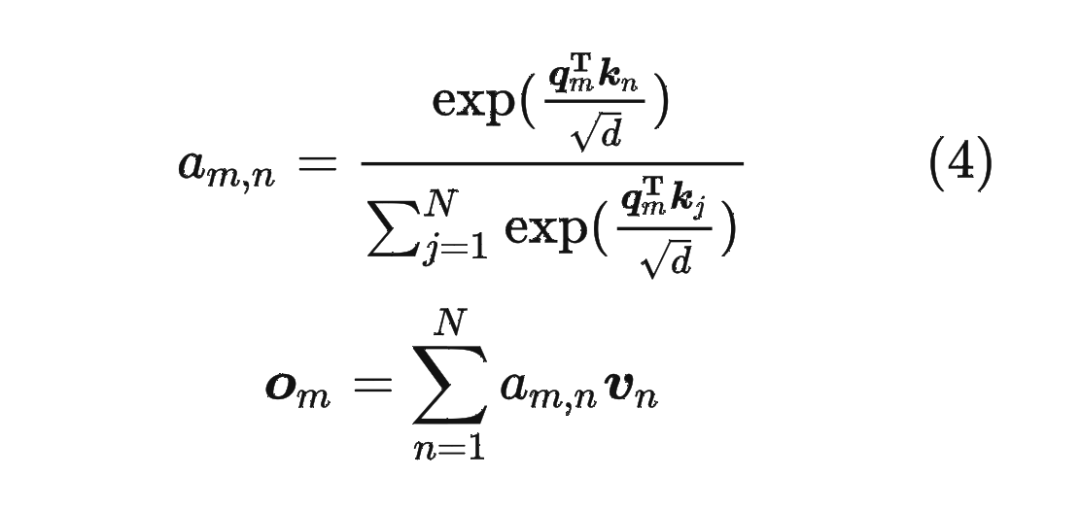
1.2 绝对位置编码
对于位置编码,常规的做法是在计算 query,key 和 value 向量之前,会计算一个位置编码向量 加到词嵌入 上,位置编码向量 同样也是 维向量,然后再乘以对应的变换矩阵 :
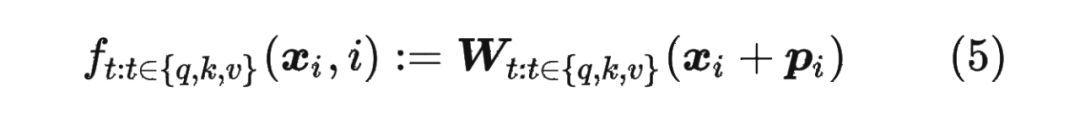
而经典的位置编码向量 的计算方式是使用 Sinusoidal 函数:
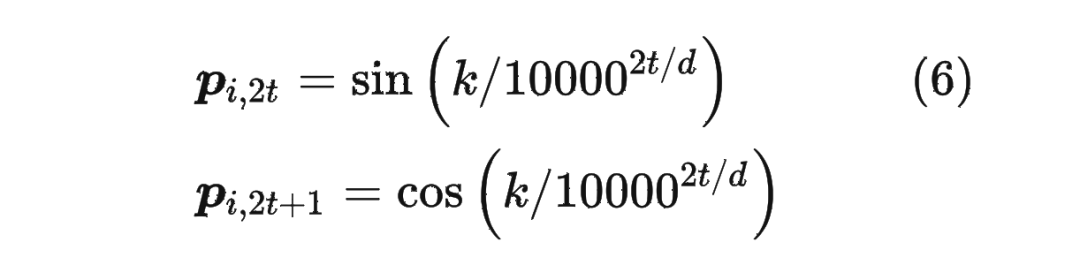
其中 表示位置 维度向量 中的第 位置分量也就是偶数索引位置的计算公式,而 就对应第 位置分量也就是奇数索引位置的计算公式。
1.3 2维旋转位置编码
论文中提出为了能利用上 token 之间的相对位置信息,假定 query 向量 和 key 向量 之间的内积操作可以被一个函数 表示,该函数 的输入是词嵌入向量 , 和它们之间的相对位置 :
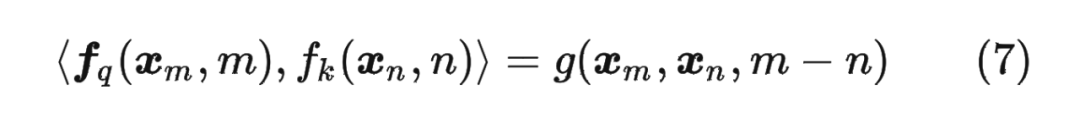 接下来的目标就是找到一个等价的位置编码方式,从而使得上述关系成立。
假定现在词嵌入向量的维度是两维 ,这样就可以利用上 2 维度平面上的向量的几何性质,然后论文中提出了一个满足上述关系的 和 的形式如下:
接下来的目标就是找到一个等价的位置编码方式,从而使得上述关系成立。
假定现在词嵌入向量的维度是两维 ,这样就可以利用上 2 维度平面上的向量的几何性质,然后论文中提出了一个满足上述关系的 和 的形式如下: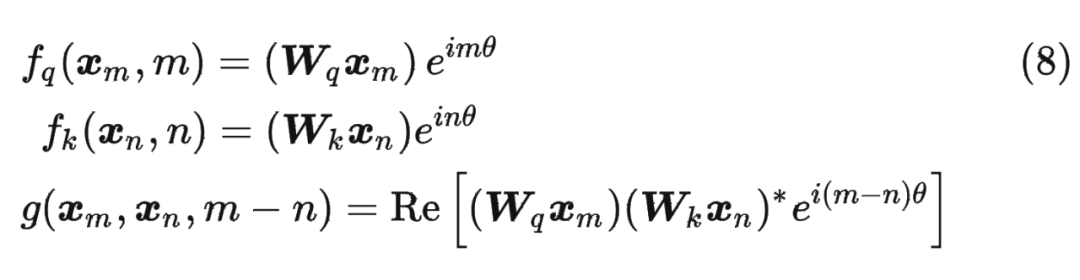 这里面 Re 表示复数的实部。
进一步地, 可以表示成下面的式子:
这里面 Re 表示复数的实部。
进一步地, 可以表示成下面的式子: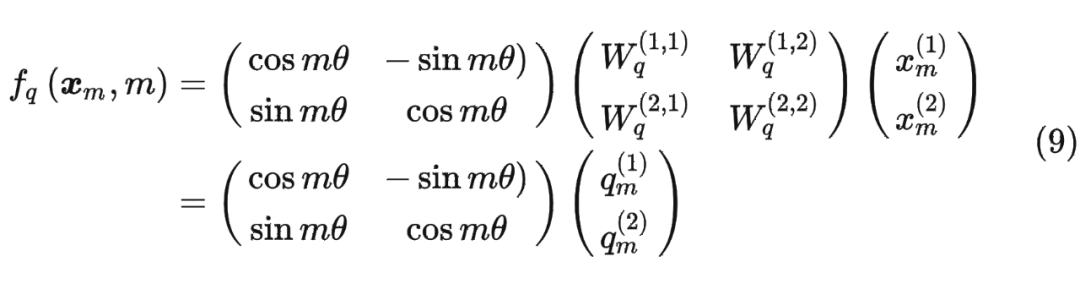 看到这里会发现,这不就是 query 向量乘以了一个旋转矩阵吗?这就是为什么叫做旋转位置编码的原因。
同理, 可以表示成下面的式子:
看到这里会发现,这不就是 query 向量乘以了一个旋转矩阵吗?这就是为什么叫做旋转位置编码的原因。
同理, 可以表示成下面的式子: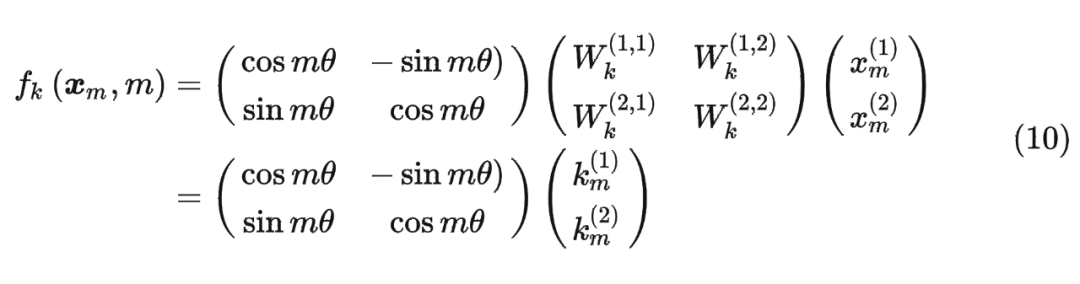 最终 可以表示如下:
最终 可以表示如下:
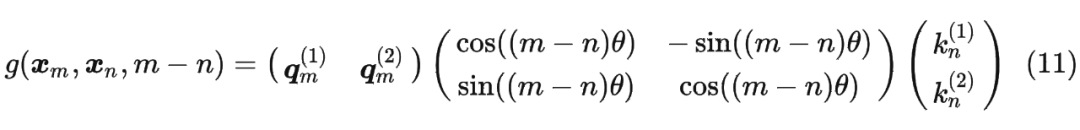
将2维推广到任意维度,可以表示如下:
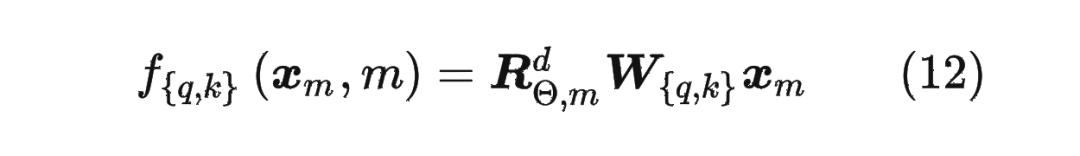 内积满足线性叠加性,因此任意偶数维的 RoPE,我们都可以表示为二维情形的拼接,即
内积满足线性叠加性,因此任意偶数维的 RoPE,我们都可以表示为二维情形的拼接,即 将 RoPE 应用到前面公式(4)的 Self-Attention 计算,可以得到包含相对位置信息的 Self-Attetion:
将 RoPE 应用到前面公式(4)的 Self-Attention 计算,可以得到包含相对位置信息的 Self-Attetion: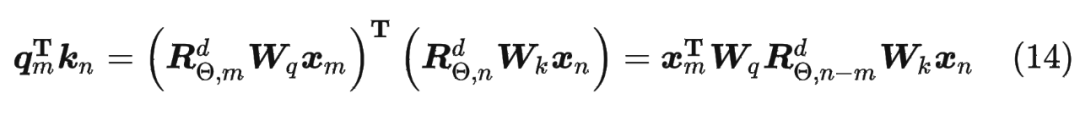
其中,。
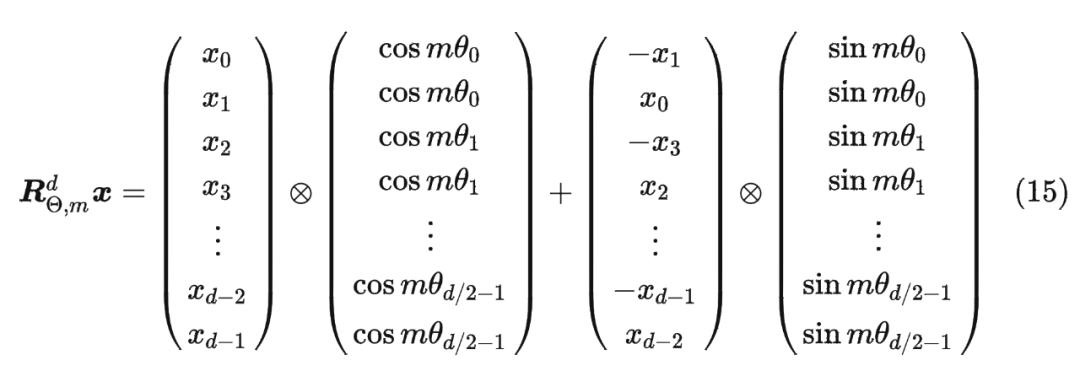
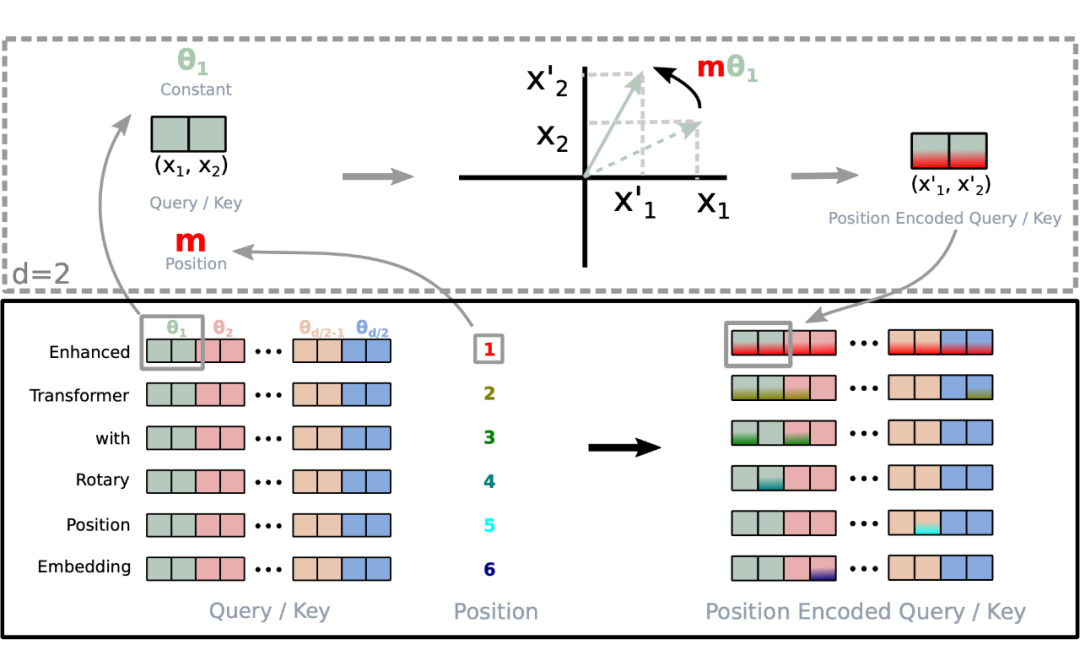
值得指出的是,由于 是一个正交矩阵,它不会改变向量的模长,因此通常来说它不会改变原模型的稳定性。 1.5 RoPE 的高效计算由于 的稀疏性,所以直接用矩阵乘法来实现会很浪费算力,推荐通过下述方式来实现 RoPE:
1.6 远程衰减
可以看到,RoPE 形式上和前面公式(6)Sinusoidal 位置编码有点相似,只不过 Sinusoidal 位置编码是加性的,而 RoPE 可以视为乘性的。在 的选择上,RoPE 同样沿用了 Sinusoidal 位置编码的方案,即 ,它可以带来一定的远程衰减性。
具体证明如下:将 两两分组后,它们加上 RoPE 后的内积可以用复数乘法表示为:
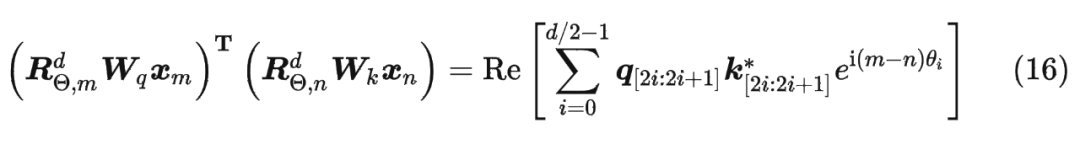
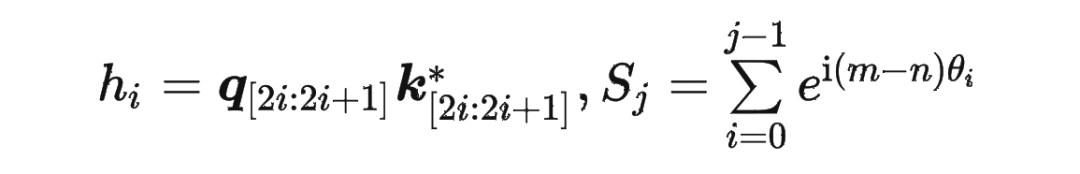
并约定 ,那么由 Abel 变换(分部求和法)可以得到:
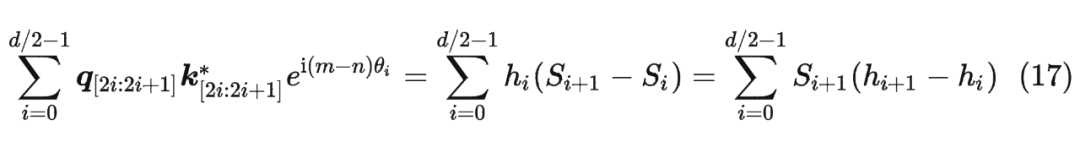
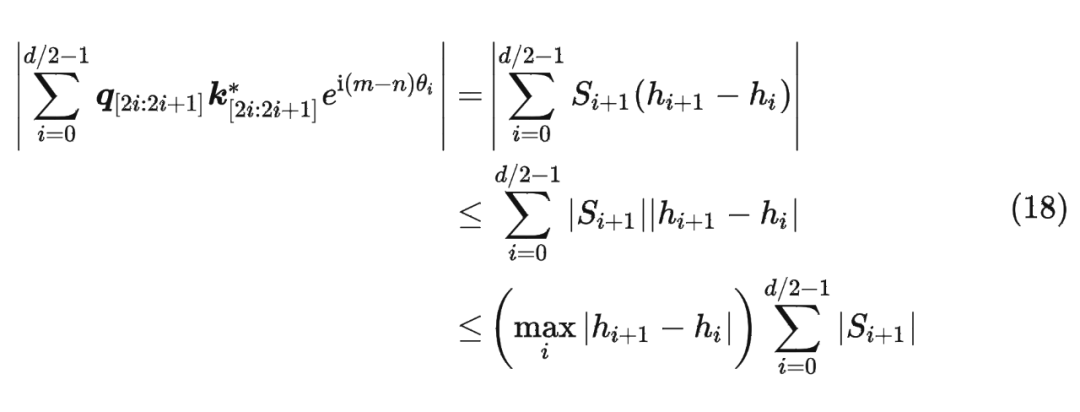
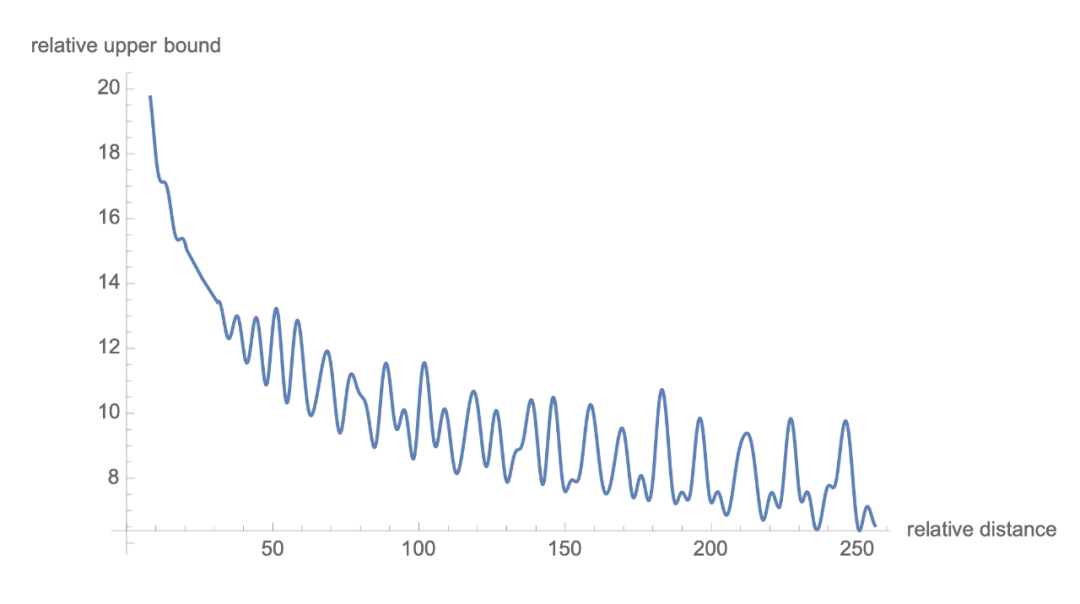
RoPE实验
我们看一下 RoPE 在预训练阶段的实验效果:
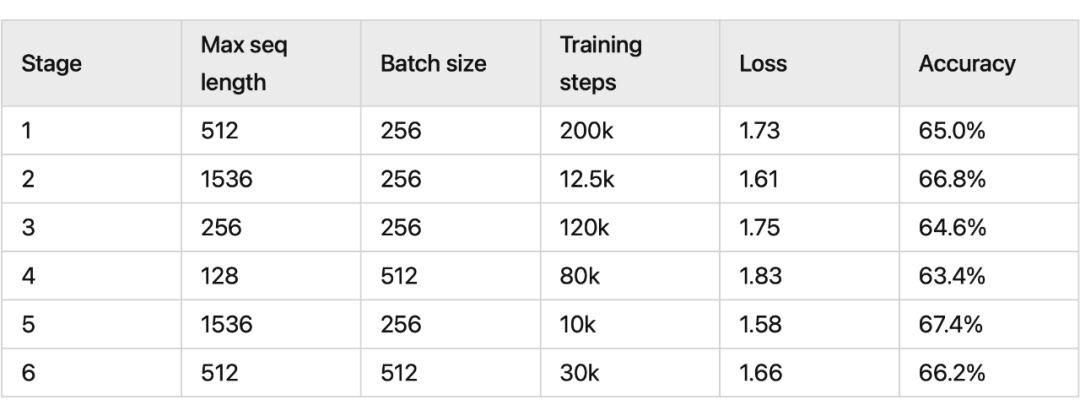
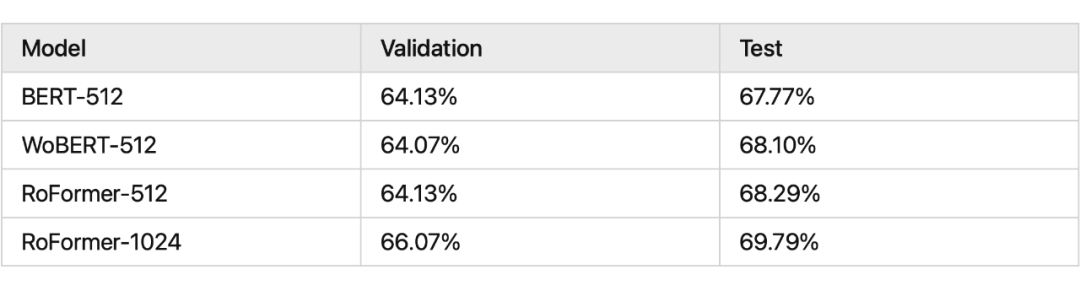 其中 RoFormer 是一个绝对位置编码替换为 RoPE 的 WoBERT 模型,后面的参数(512)是微调时截断的maxlen,可以看到 RoPE 确实能较好地处理长文本语义。
其中 RoFormer 是一个绝对位置编码替换为 RoPE 的 WoBERT 模型,后面的参数(512)是微调时截断的maxlen,可以看到 RoPE 确实能较好地处理长文本语义。
RoPE代码实现
Meta 的 LLAMA 和 清华的 ChatGLM 都使用了 RoPE 编码,下面看一下具体实现。
3.1 在LLAMA中的实现
# 生成旋转矩阵
def precompute_freqs_cis(dim: int, seq_len: int, theta: float = 10000.0):
# 计算词向量元素两两分组之后,每组元素对应的旋转角度 heta_i
freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
# 生成 token 序列索引 t = [0, 1,..., seq_len-1]
t = torch.arange(seq_len, device=freqs.device)
# freqs.shape = [seq_len, dim // 2]
freqs = torch.outer(t, freqs).float() # 计算m * heta
# 计算结果是个复数向量
# 假设 freqs = [x, y]
# 则 freqs_cis = [cos(x) + sin(x)i, cos(y) + sin(y)i]
freqs_cis = torch.polar(torch.ones_like(freqs), freqs)
return freqs_cis
# 旋转位置编码计算
def apply_rotary_emb(
xq: torch.Tensor,
xk: torch.Tensor,
freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
# xq.shape = [batch_size, seq_len, dim]
# xq_.shape = [batch_size, seq_len, dim // 2, 2]
xq_ = xq.float().reshape(*xq.shape[:-1], -1, 2)
xk_ = xk.float().reshape(*xk.shape[:-1], -1, 2)
# 转为复数域
xq_ = torch.view_as_complex(xq_)
xk_ = torch.view_as_complex(xk_)
# 应用旋转操作,然后将结果转回实数域
# xq_out.shape = [batch_size, seq_len, dim]
xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(2)
xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(2)
return xq_out.type_as(xq), xk_out.type_as(xk)
class Attention(nn.Module):
def __init__(self, args: ModelArgs):
super().__init__()
self.wq = Linear(...)
self.wk = Linear(...)
self.wv = Linear(...)
self.freqs_cis = precompute_freqs_cis(dim, max_seq_len * 2)
def forward(self, x: torch.Tensor):
bsz, seqlen, _ = x.shape
xq, xk, xv = self.wq(x), self.wk(x), self.wv(x)
xq = xq.view(batch_size, seq_len, dim)
xk = xk.view(batch_size, seq_len, dim)
xv = xv.view(batch_size, seq_len, dim)
# attention 操作之前,应用旋转位置编码
xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis)
# scores.shape = (bs, seqlen, seqlen)
scores = torch.matmul(xq, xk.transpose(1, 2)) / math.sqrt(dim)
scores = F.softmax(scores.float(), dim=-1)
output = torch.matmul(scores, xv) # (batch_size, seq_len, dim)
# ......
这里举一个例子,假设 batch_size=10, seq_len=3, d=8,则调用函数 precompute_freqs_cis(d, seq_len) 后,生成结果为:
In [239]: freqs_cis
Out[239]:
tensor([[ 1.0000+0.0000j, 1.0000+0.0000j, 1.0000+0.0000j, 1.0000+0.0000j],
[ 0.5403+0.8415j, 0.9950+0.0998j, 0.9999+0.0100j, 1.0000+0.0010j],
[-0.4161+0.9093j, 0.9801+0.1987j, 0.9998+0.0200j, 1.0000+0.0020j]])
以结果中的第二行为例(对应的 m = 1),也就是:
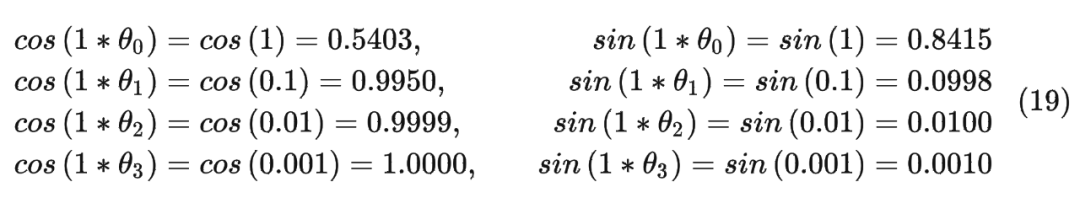 最终按照公式(12)可以得到编码之后的 。
注意:在代码中是直接用 freqs_cis[0] * xq_[0] 的结果表示第一个 token 对应的旋转编码(和公式 12 计算方式有所区别)。其中将原始的 query 向量 转换为了复数形式。
最终按照公式(12)可以得到编码之后的 。
注意:在代码中是直接用 freqs_cis[0] * xq_[0] 的结果表示第一个 token 对应的旋转编码(和公式 12 计算方式有所区别)。其中将原始的 query 向量 转换为了复数形式。
In [351]: q_ = q.float().reshape(*q.shape[:-1], -1, 2)
In [352]: q_[0]
Out[352]:
tensor([[[ 1.0247, 0.4782],
[ 1.5593, 0.2119],
[ 0.4175, 0.5309],
[ 0.4858, 0.1850]],
[[-1.7456, 0.6849],
[ 0.3844, 1.1492],
[ 0.1700, 0.2106],
[ 0.5433, 0.2261]],
[[-1.1206, 0.6969],
[ 0.8371, -0.7765],
[-0.3076, 0.1704],
[-0.5999, -1.7029]]])
In [353]: xq = torch.view_as_complex(q_)
In [354]: xq[0]
Out[354]:
tensor([[ 1.0247+0.4782j, 1.5593+0.2119j, 0.4175+0.5309j, 0.4858+0.1850j],
[-1.7456+0.6849j, 0.3844+1.1492j, 0.1700+0.2106j, 0.5433+0.2261j],
[-1.1206+0.6969j, 0.8371-0.7765j, -0.3076+0.1704j, -0.5999-1.7029j]])
这里为什么可以这样计算?
主要是利用了复数的乘法性质。
我们首先来复习一下复数乘法的性质:
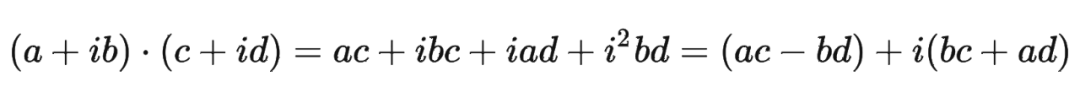
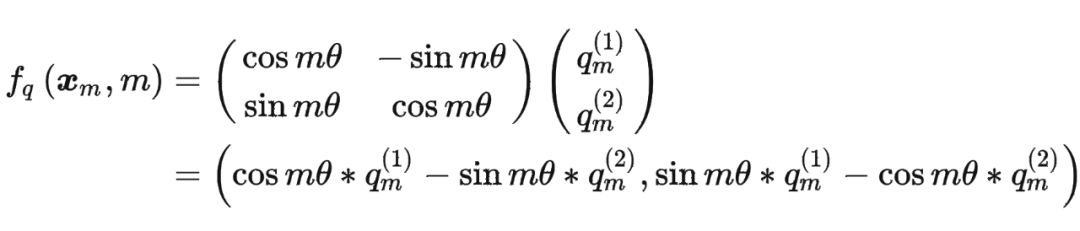
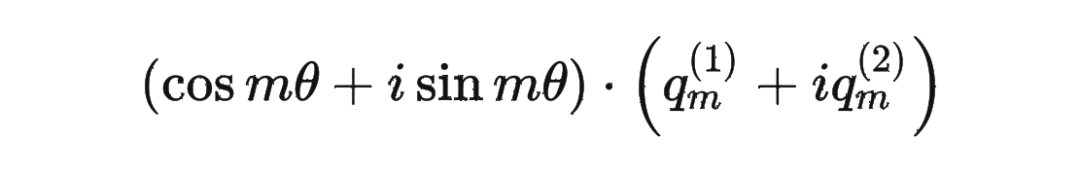
class RotaryEmbedding(torch.nn.Module):
def __init__(self, dim, base=10000, precision=torch.half, learnable=False):
super().__init__()
# 计算 heta_i
inv_freq = 1. / (base ** (torch.arange(0, dim, 2).float() / dim))
inv_freq = inv_freq.half()
self.learnable = learnable
if learnable:
self.inv_freq = torch.nn.Parameter(inv_freq)
self.max_seq_len_cached = None
else:
self.register_buffer('inv_freq', inv_freq)
self.max_seq_len_cached = None
self.cos_cached = None
self.sin_cached = None
self.precision = precision
def forward(self, x, seq_dim=1, seq_len=None):
if seq_len is None:
seq_len = x.shape[seq_dim]
if self.max_seq_len_cached is None or (seq_len > self.max_seq_len_cached):
self.max_seq_len_cached = None if self.learnable else seq_len
# 生成 token 序列索引 t = [0, 1,..., seq_len-1]
t = torch.arange(seq_len, device=x.device, dtype=self.inv_freq.dtype)
# 对应m * heta
freqs = torch.einsum('i,j->ij', t, self.inv_freq)
# 将 m * heta 拼接两次,对应复数的实部和虚部
emb = torch.cat((freqs, freqs), dim=-1).to(x.device)
if self.precision == torch.bfloat16:
emb = emb.float()
# [sx, 1 (b * np), hn]
cos_cached = emb.cos()[:, None, :] # 计算得到cos(m* heta)
sin_cached = emb.sin()[:, None, :] # 计算得到cos(m* heta)
if self.precision == torch.bfloat16:
cos_cached = cos_cached.bfloat16()
sin_cached = sin_cached.bfloat16()
if self.learnable:
return cos_cached, sin_cached
self.cos_cached, self.sin_cached = cos_cached, sin_cached
return self.cos_cached[:seq_len, ...], self.sin_cached[:seq_len, ...]
def _apply(self, fn):
if self.cos_cached is not None:
self.cos_cached = fn(self.cos_cached)
if self.sin_cached is not None:
self.sin_cached = fn(self.sin_cached)
return super()._apply(fn)
def rotate_half(x):
x1, x2 = x[..., :x.shape[-1] // 2], x[..., x.shape[-1] // 2:]
return torch.cat((-x2, x1), dim=x1.ndim - 1)
RoPE的外推性
我们都知道 RoPE 具有很好的外推性,前面的实验结果也证明了这一点。这里解释下具体原因。 RoPE 可以通过旋转矩阵来实现位置编码的外推,即可以通过旋转矩阵来生成超过预期训练长度的位置编码。这样可以提高模型的泛化能力和鲁棒性。 我们回顾一下 RoPE 的工作原理:假设我们有一个 维的绝对位置编码 ,其中 是位置索引。我们可以将 看成一个 维空间中的一个点。我们可以定义一个 维空间中的一个旋转矩阵 ,它可以将任意一个点沿着某个轴旋转一定的角度。我们可以用 来变换 ,得到一个新的点 。我们可以发现, 和 的距离是相等的,即 。这意味着 和 的相对关系没有改变。但是, 和 的距离可能发生改变,即 。这意味着 和 的相对关系有所改变。因此,我们可以用 来调整不同位置之间的相对关系。 如果我们想要生成超过预训练长度的位置编码,我们只需要用 来重复变换最后一个预训练位置编码 ,得到新的位置编码
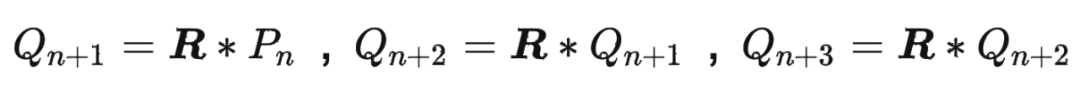 依此类推。这样就可以得到任意长度的位置编码序列 ,其中 可以大于 。由于 是一个正交矩阵,它保证了 和 的距离不会无限增大或缩小,而是在一个有限范围内波动。这样就可以避免数值溢出或下溢的问题。同时,由于 是一个可逆矩阵,它保证了 和 的距离可以通过 的逆矩阵 还原到 和 的距离,即
依此类推。这样就可以得到任意长度的位置编码序列 ,其中 可以大于 。由于 是一个正交矩阵,它保证了 和 的距离不会无限增大或缩小,而是在一个有限范围内波动。这样就可以避免数值溢出或下溢的问题。同时,由于 是一个可逆矩阵,它保证了 和 的距离可以通过 的逆矩阵 还原到 和 的距离,即
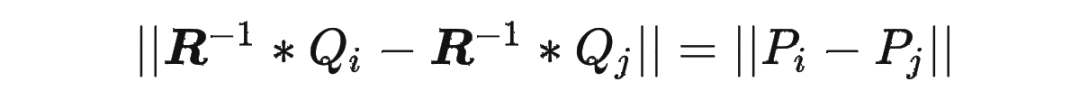
总结
最近一直听到旋转编码这个词,但是一直没有仔细看具体原理。今天花时间仔细看了一遍,确实理论写的比较完备,而且实验效果也不错。目前很多的大模型,都选择了使用了这种编码方式(LLAMA、GLM 等)。
附录
这里补充一下前面公式 1.3.2 节中,公式(8)~(11)是怎么推导出来的。 回到之前的公式(8),编码之后的 以及内积 的形式如下:
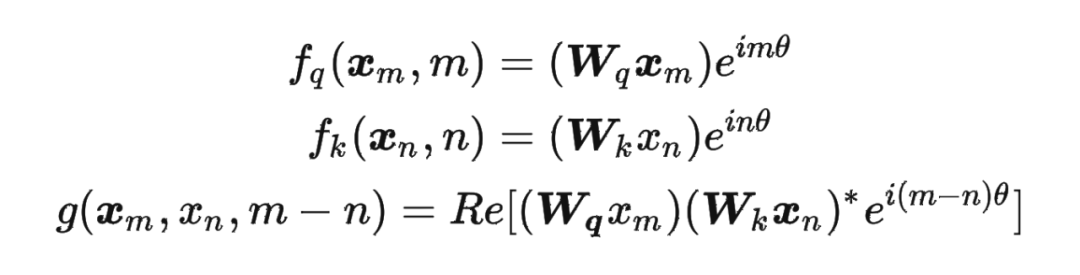
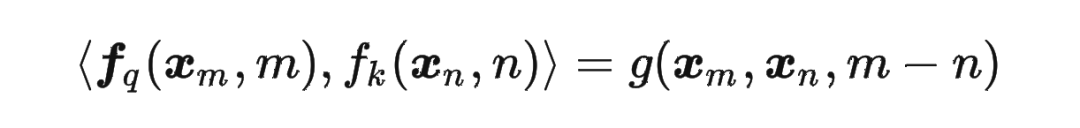
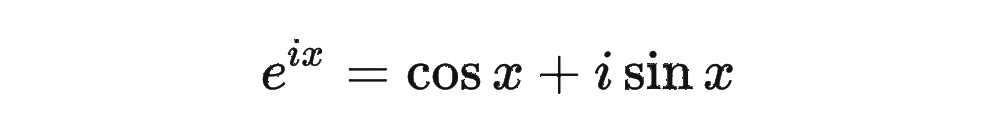
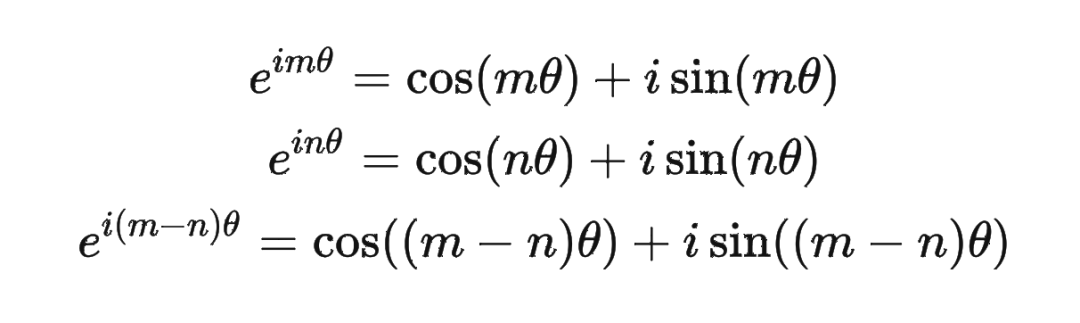 然后我们看回公式:
然后我们看回公式: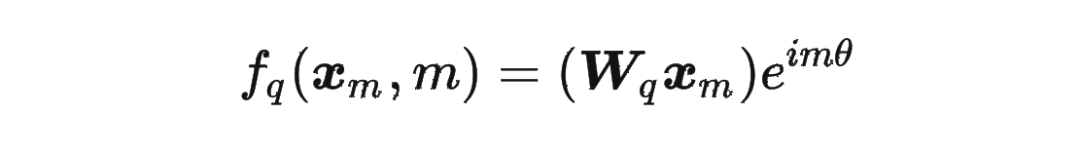 其中 是个二维矩阵, 是个二维向量,相乘的结果也是一个二维向量,这里用 表示:
其中 是个二维矩阵, 是个二维向量,相乘的结果也是一个二维向量,这里用 表示:
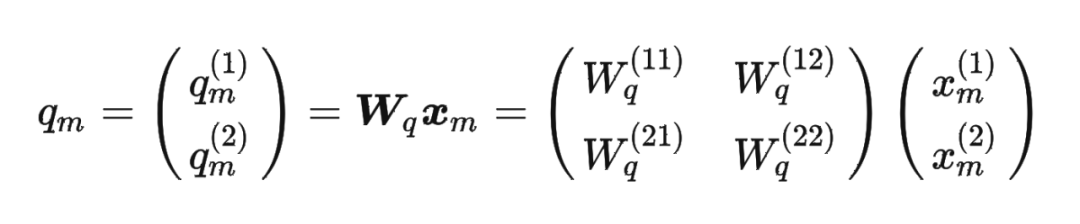
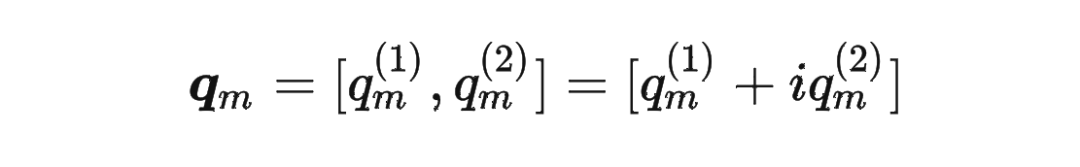 接着
接着
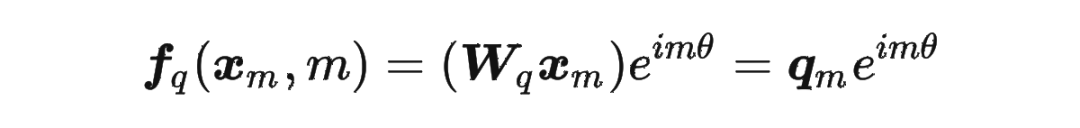
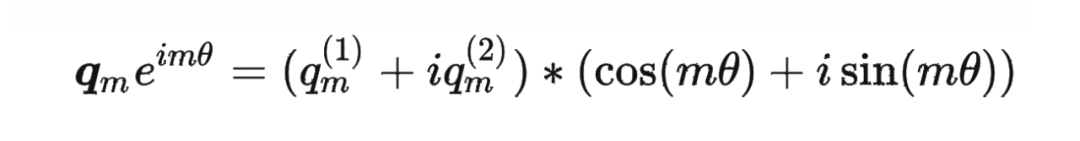
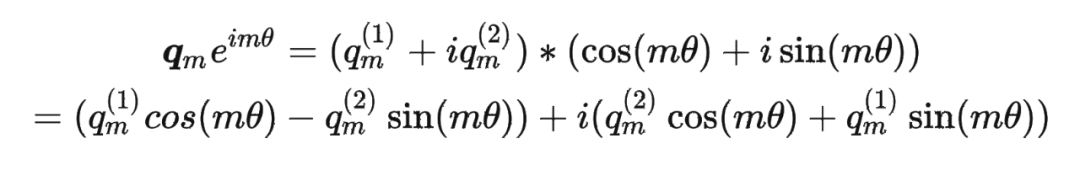
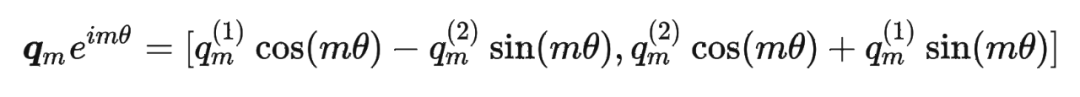
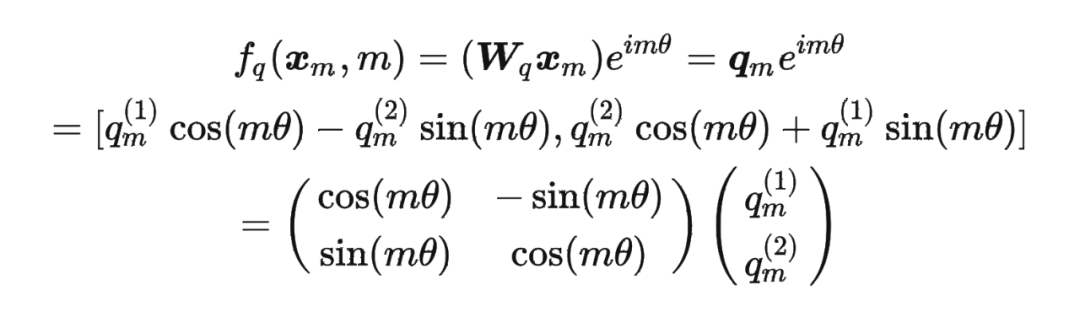
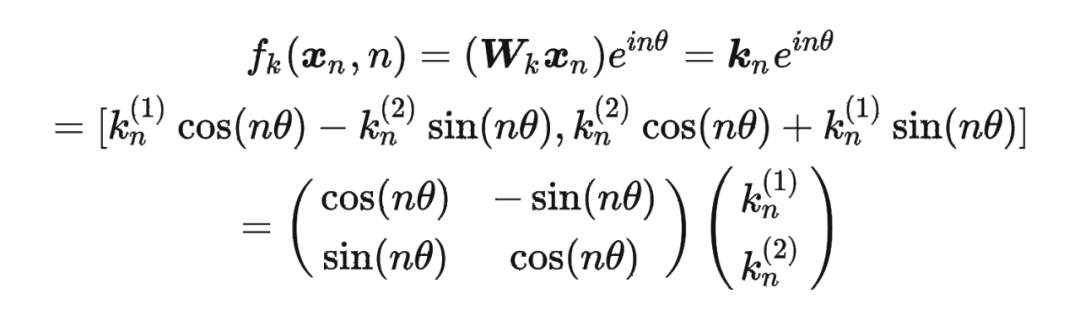
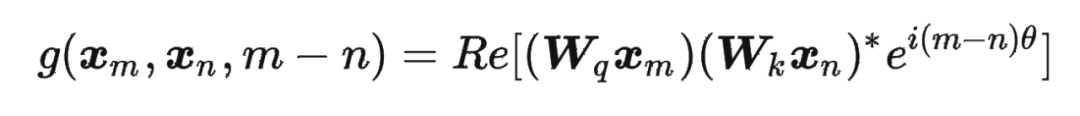 其中 表示一个复数 的实部部分,而 则表示复数 的共轭。
复习一下共轭复数的定义:
其中 表示一个复数 的实部部分,而 则表示复数 的共轭。
复习一下共轭复数的定义:
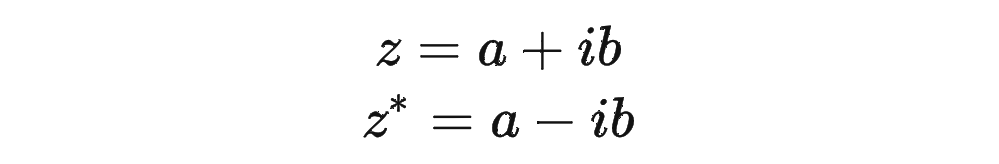
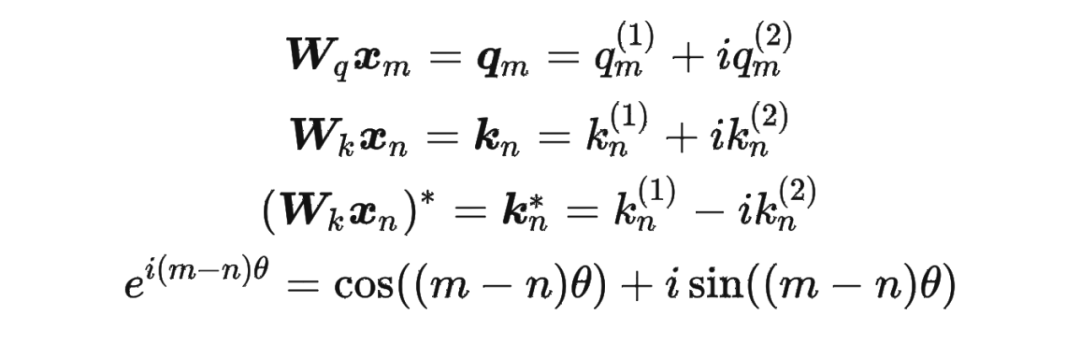
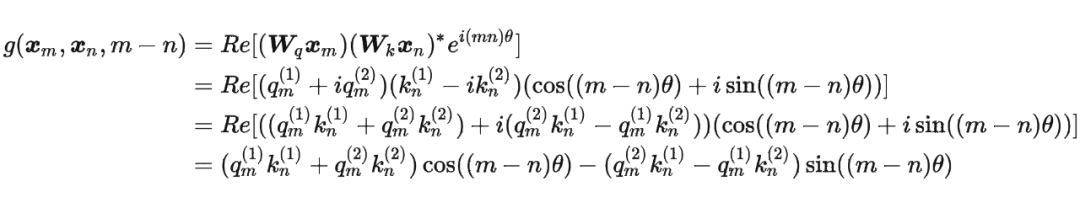
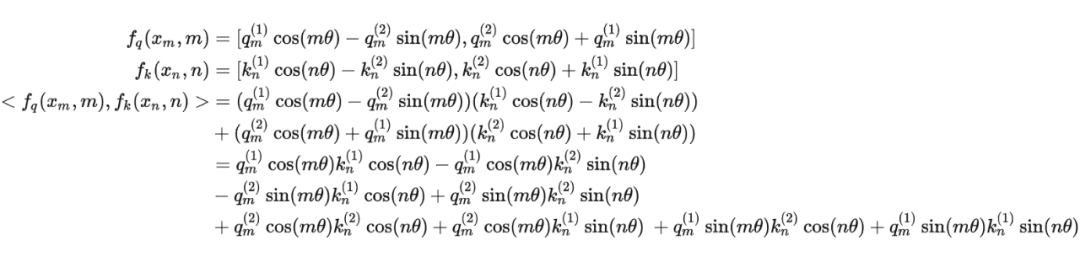
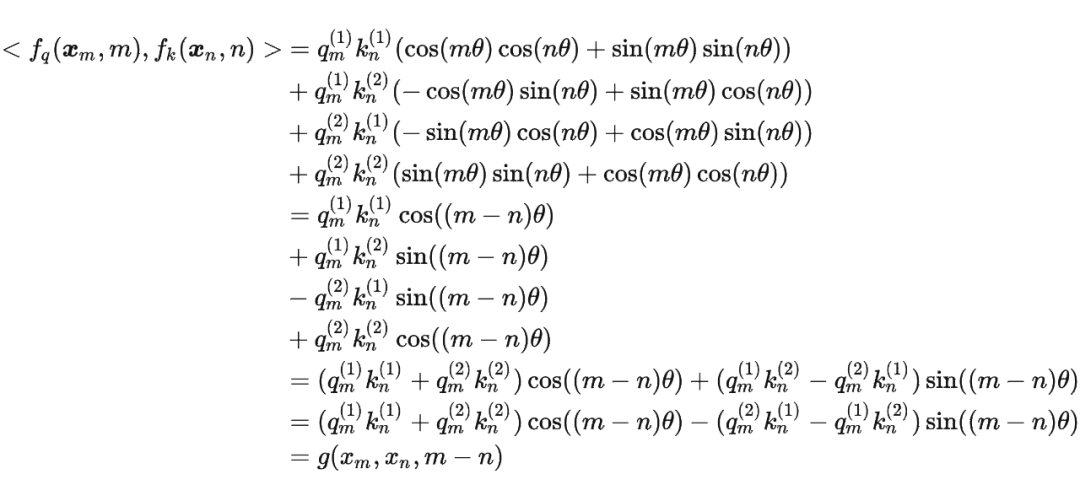
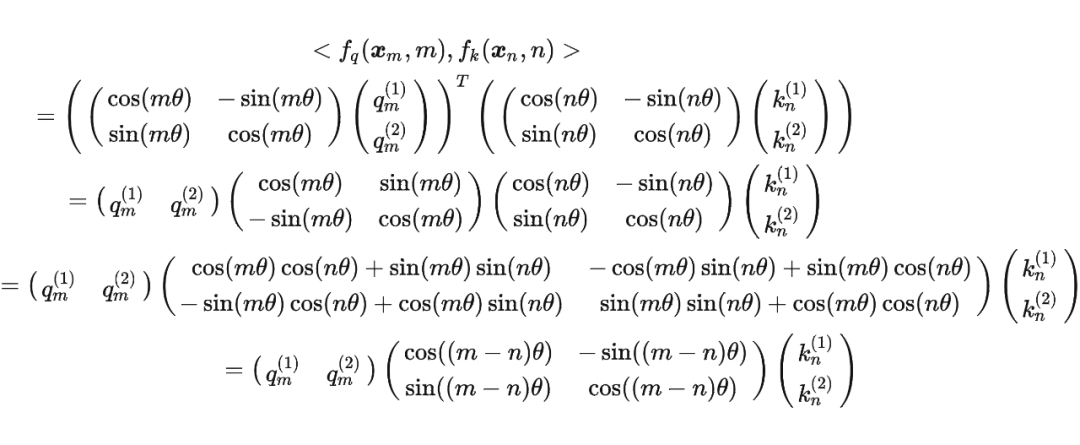
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
遇到SE5经常自动重启,大约十几分钟到二十分钟左右重启一次的问题如何解决?2023-09-18 920
-
基于STM32F103RB的数码管如何去实现十分钟计时呢2021-11-17 1233
-
BearPi-HM Nano 十分钟上手教程资料2021-04-13 11093
-
十分钟分析稳压三极管工作原理资料下载2021-04-11 1059
-
英国搭建太阳能汽车充电网试点项目,电动汽车在三十分钟内完成充电2019-04-06 3571
-
三星改革智能手机充电技术,充满只需十分钟2017-12-02 2341
-
采集系统需要隔十分钟采集10S数据,怎么实现?2017-01-13 4170
-
快充技术&芯片详解 十分钟让你的手机满血复活2016-06-23 67801
-
全球首发十分钟快速充满电移动电源2015-03-25 4106
-
十分钟学会ISE2013-03-26 14083
-
ModelSim SE 十分钟入门2012-08-12 3074
-
十分钟学会Xilinx FPGA 设计1.12012-08-10 3598
-
十分钟学会Xilinx FPGA 设计2010-03-15 873
全部0条评论

快来发表一下你的评论吧 !

