

什么是RC相移振荡器?什么是文氏桥振荡器?
电子说
描述
之前介绍过:由电阻、电容组成的RC电路可以做成滤波器。滤波器对不同频率信号施加影响,在改变信号幅度的同时,也改变了信号的相位。就是这个“相移”特性,可以在振荡器中派上用场。
一、RC电路的“相移”特性(Phase shift)
我们构建简单的RC电路,输入交流信号,查看输出波形如下:
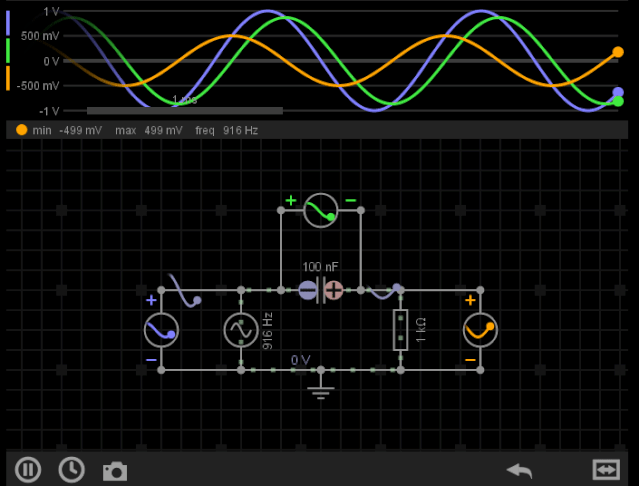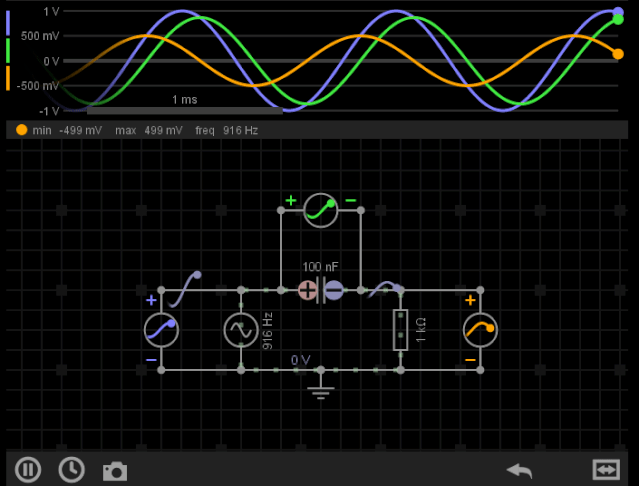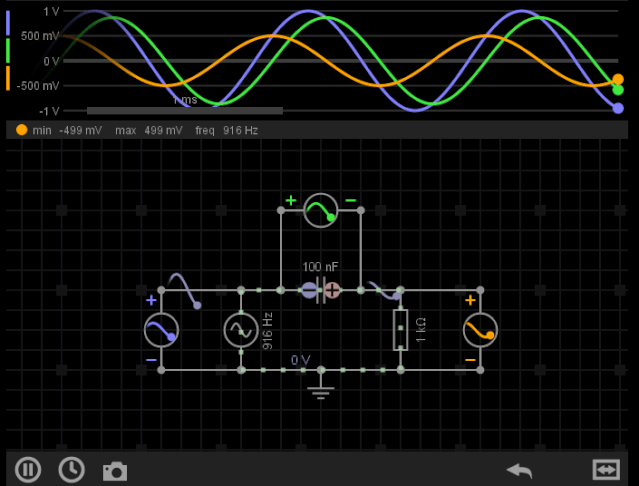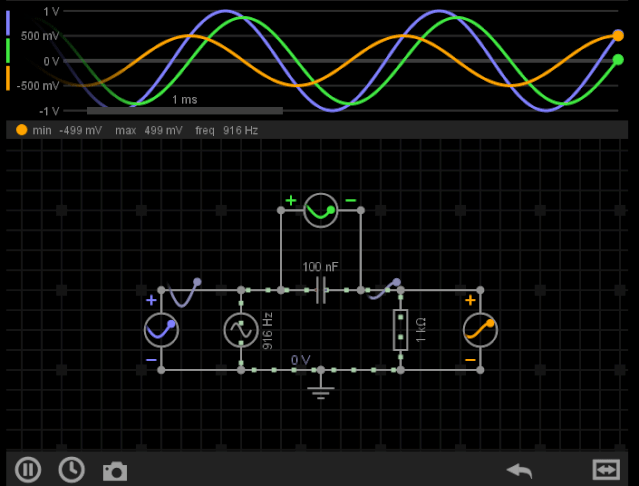
图1-RC“相移”特性(Phase shift)
可以看到R作为输出(黄色),相比输入信号(蓝色),它有明显的相移(滞后),幅度也有所改变。
通过阻抗公式计算如下,幅度就是分压,相位上就是阻抗的实部与虚部之比:

图2-输出信号阻抗分压和相位计算
以上计算是针对某一个特定频率的信号,如果要描述RC电路对各个频率信号的影响,那就要使用频谱图查看:

图3-RC频谱图(高通滤波器)
上述频谱图中,上、下两个图分别描述对不同频率信号幅度的影响,以及对相位的影响。可见,RC电路是一个高通滤波器。
二、RC相移振荡器(RC Phase Shift Oscillator)
从前一篇文章所述,振荡器模型由放大器和反馈网络组成:

图4-振荡器模型
它遵循Barkhausen(巴克豪森)准则:
- 回路增益≥1;
- Vin/Vfeedback相位一致,形成正反馈;
假设经由放大器,信号相位改变180°,那么反馈网络所需相移也是180°。这个“相移”操作就可以由RC电路完成。如果一个RC电路无法所需角度,那就由多个RC电路级联而成:

图5-单个RC电路相移效果和多个RC电路级联相移效果
理论上,单个RC电路所能达到的相移最大是90°(R很小,C很大的情况)。要完成180°相移,一般设置3个RC电路级联,每个RC电路完成60°相移,共计180°。
我们来看一下,由RC和NPN三极管构建的RC振荡器电路如下:

图6-RC相移振荡器
这和前一篇所说的电容/电感三点式振荡器很像,只是将LC部分改成了3个RC级联组成的相移网络。
对于这种电路,振荡频率为:

图7-RC相移振荡器的振荡频率
其中,N表示RC电路的级联个数。
三、文氏桥振荡器(Wien Bridge Oscillator)
文氏桥由两个RC电路组成,其中是一个RC串联电路,形成高通滤波器,另一个是RC并联电路,形成低通滤波器:

图8-文氏桥电路
信号先经过高通滤波器,过滤掉低频信号;再经过低通滤波器,过滤到高频信号;最后,只有一个(区域)特定频率的信号在输出端得以保留,且其相位不变:

图9-文氏桥电路的频率响应特性
文氏桥振荡器,由文氏桥电路加上一个同相运放组成:

图10-文氏桥振荡器
运放的同相输入端由文氏桥电路阻抗分压而成,在R1=R2,C1=C2情况下,Zp/(Zp+Zs)=1/3。由此设置运放电阻R3和R4,满足回路增益≥1即可。
实际上,文氏桥振荡器刚出现时,R4由钨丝灯代替:

图11-经典文氏桥振荡器
钨丝灯实现了自动增益调整的功能:刚开始上电钨丝灯电阻小,运放增益大,具有起振效果;随着运行时间变长,钨丝灯发热,电阻上升,运放增益下降,获得稳定的振荡波形。
最后让我们来看一个文氏桥振荡器的仿真效果:
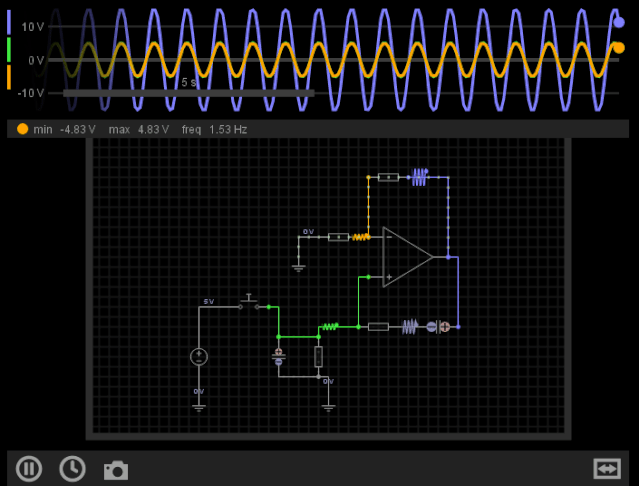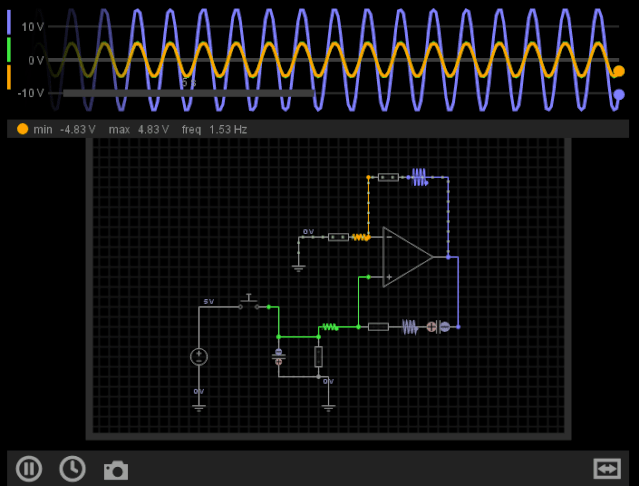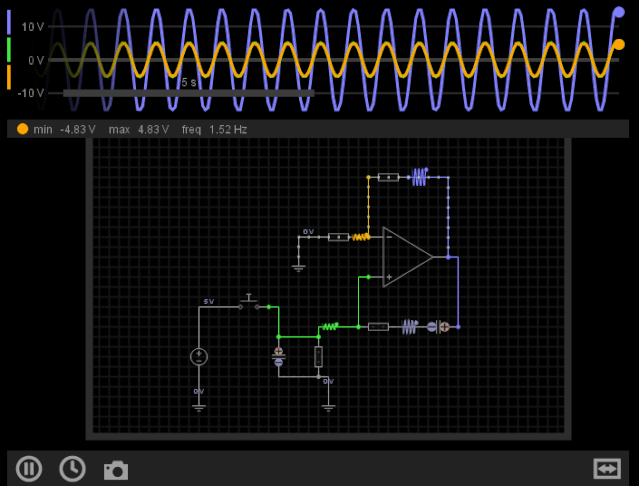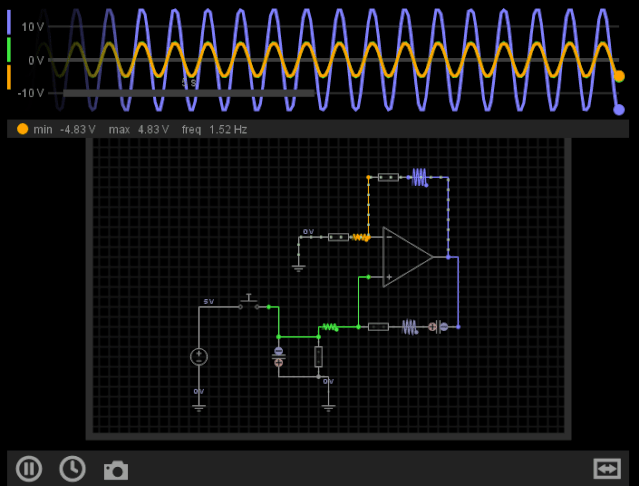
图12-文氏桥振荡器的仿真效果
四、总结
今天介绍了以RC为基础的振荡器,相比于LC振荡器,由于没有使用电感,它克服了电感的体积大、成本高的缺点,在低频信号中得以广泛应用。
-
文氏桥振荡器的原理和应用2024-07-30 7234
-
RC相移振荡器电路图分享2024-02-26 9377
-
什么是RC振荡器?RC振荡器的工作原理 基本RC振荡器电路设计2023-08-31 10263
-
使用运算放大器的RC相移振荡器2022-09-01 5099
-
AN-111:单电源文氏桥振荡器2021-05-07 923
-
RC相移振荡器课程设计2016-12-29 1116
-
基于文氏振荡器的D类放大器2011-09-02 1455
-
宽频段的文氏桥振荡器电路2010-02-25 3055
-
低频文氏桥振荡器2009-04-08 1316
-
文氏桥振荡器电路图2009-03-23 1623
-
集成运放组成的文氏桥振荡器2009-03-09 6159
全部0条评论

快来发表一下你的评论吧 !

