FPGA设计中二分法查表算法的实现

二分化查找算法是在软件中广泛应用的一种算法，那么在FPGA的设计中是否可以用这种算法呢？什么场景下会可能用到这种算法呢？

二分法简介

这里先简单的说明下二分法查找，不涉及具体的算法原理。要实现二分法查表，有一个前提，那就是这个表是一个有序表。

假定表的深度为N（从0到N-1），那么首先从N/2地址读出内容比较，如果待比较的值x比从表中读出的值M小，说明x只可能位于0——（N/2-1）之间，然后采用同样的方式从0——（N/2-1）中继续查找；如果待比较的值x比从表中读出的值M大，说明x只可能位于（N/2+1)——N-1之间，然后采用同样的方式从（N/2+1)——N-1中继续查找。

应用场景

在FPGA设计中，什么场景可以用到二分法查找呢？只有一个条件，那就是表项是一个有序表。要得到一个有序表，有几种情况：

1、表项由逻辑实现写操作，那么在写入的过程中，先要把表项中的内容读出来，和即将要写入的内容做排序后，再写回。这种方案相对来说还是比较复杂的，尤其是在高性能的场景下。

2、表项由CPU实现写操作，如果表项不需要动态更新，那这就是一件很容易的事情了，如果表项需要CPU来更新，那么也需要将表项读出来后进行排序然后再写入FPGA。

在网络通信中，有如下一种场景，就是收到的报文依据源IP地址进行过滤（不是真正意义上的防火墙），只允许特定的IP地址通过，IP地址的个数最多为1024个，由软件来维护。当然可以采用hash算法，实现稍微复杂点，也可以采用最原始的办法，就是把每个IP地址读出来比较，这种方案性能不稳定，最差的情况有可能需要1024个cycle才能出结果。如果用二分法查找，最多只需要10次就可以出结果。

实现方案

知道了原理，其实该算法的方案实现是比较简单的，就是通过跳表项的读地址来实现比较，如下图所示：

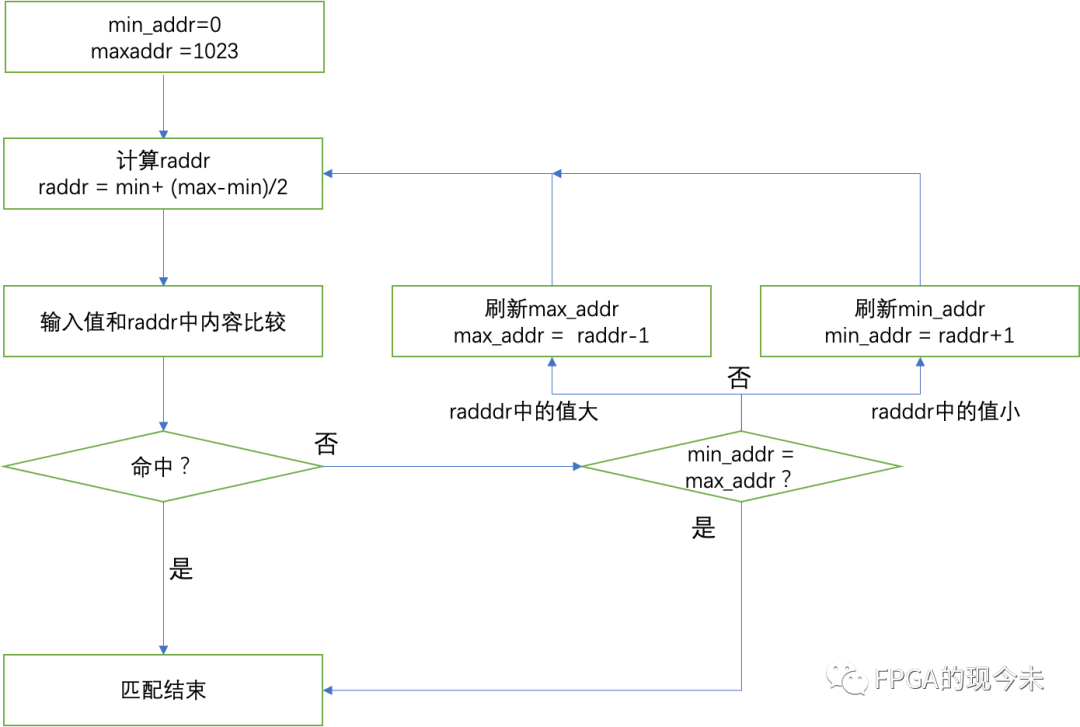
对min_addr和max_addr初始化后，计算出raddr，然后从raddr中读出数据比较比较后，根据比较的结果来刷新min_addr或者max_addr，然后重新计算raddr的值，直到匹配中，或者min_addr=max_addr。

总结

在FPGA中需要查找的表项，如果能实现有序排列，采用二分法查找是一个不错的选择。相比其他算法，它在性能上保持一定优势的前提下，实现也比较简单。