一文捋顺千亿模型训练技术：流水线并行、张量并行和3D并行

 

导读

流水线性并行、张量并行、3D并行三种分布式训练方法的详细解读，从原理到具体方法案例。 

流水线性并行和张量并行都是对模型本身进行划分，目的是利用有限的单卡显存训练更大的模型。简单来说，流水线并行水平划分模型，即按照层对模型进行划分；张量并行则是垂直划分模型。3D并行则是将流行线并行、张量并行和数据并行同时应用到模型训练中。

一、流水线并行

流水线并行的目标是训练更大的模型。本小节先介绍符合直觉的朴素层并行方法，并分析其局限性。然后，介绍流水线并行算法GPipe和PipeDream。

1. 朴素层并行

当一个模型大到单个GPU无法训练时，最直接的想法是对模型层进行划分，然后将划分后的部分放置在不同的GPU上。下面以一个4层的序列模型为例，介绍朴素层并行：

 

将其按层划分至两个GPU上：

• GPU1负责计算：intermediate  (input)) ;
• GPU2负责计算：output  (intermediate ;

动图

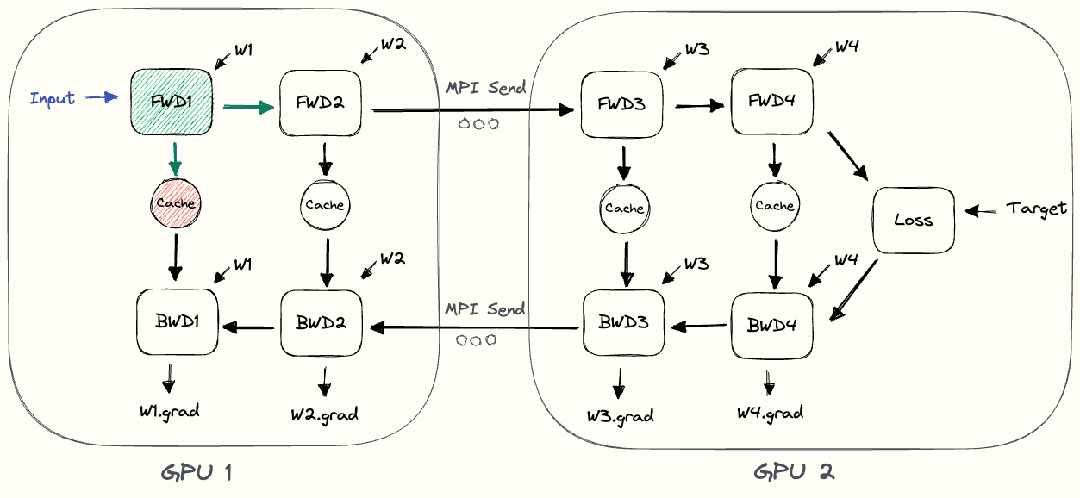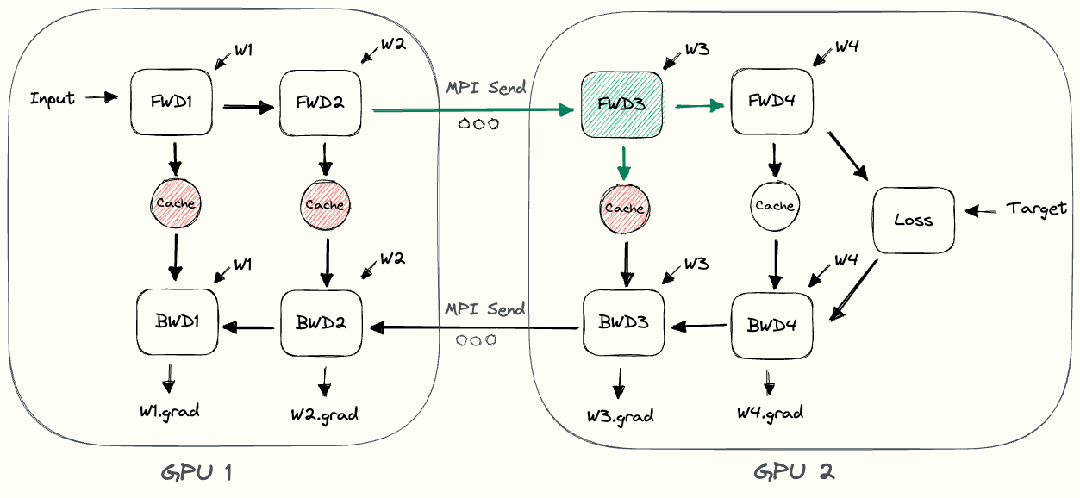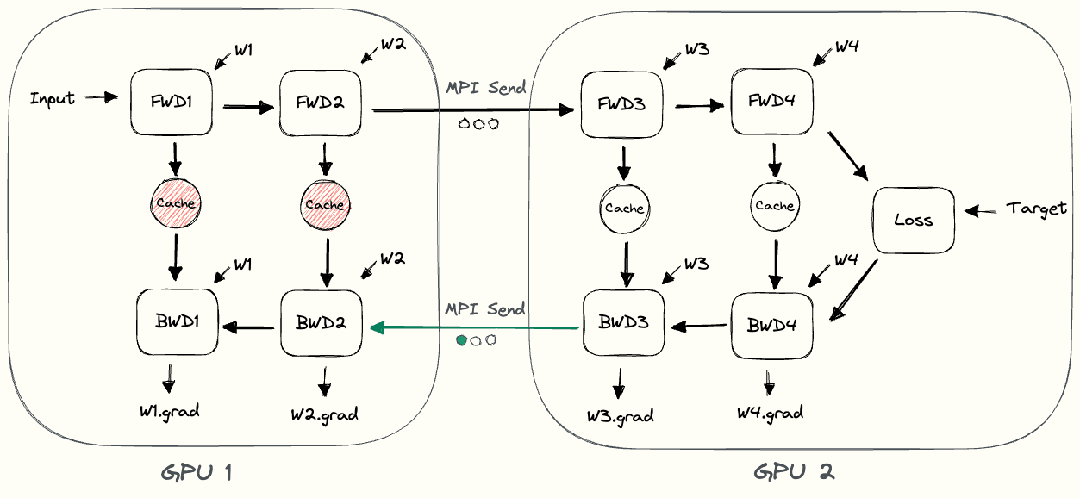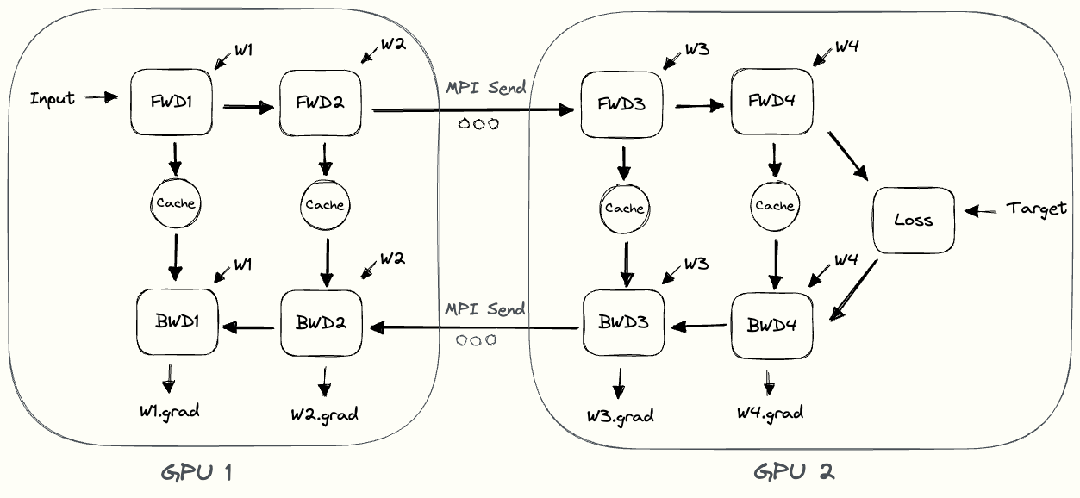
整个朴素层并行前向传播和后向传播的过程如上图所示。GPU1执行前向传播, 并将激活 (activations)缓存下来。然后将  层的输出intermediate发送给GPU2, GPU2完成前向传播和loss计算后, 开始反向传播。当GPU2完成反向传播后, 会将  的梯度返还给GPU1。GPU1完成最终的反向传播。

根据上面的介绍，可以发现朴素层并行的缺点：

• 低GPU利用率。在任意时刻，有且仅有一个GPU在工作，其他GPU都是空闲的。
• 计算和通信没有重叠。在发送前向传播的中间结果(FWD)或者反向传播的中间结果(BWD)时，GPU也是空闲的。
• 高显存占用。GPU1需要保存整个minibatch的所有激活，直至最后完成参数更新。如果batch size很大，这将对显存带来巨大的挑战。

2. GPipe

2.1 GPipe的原理

GPipe通过将minibatch划分为更小且相等尺寸的microbatch来提高效率。具体来说，让每个microbatch独立的计算前后向传播，然后将每个mircobatch的梯度相加，就能得到整个batch的梯度。由于每个层仅在一个GPU上，对mircobatch的梯度求和仅需要在本地进行即可，不需要通信。

假设有4个GPU，并将模型按层划分为4个部分。朴素层并行的过程为

Timestep	0	1	2	3	4	5	6	7
GPU3				FWD	BWD
GPU2			FWD			BWD
GPU1		FWD					BWD
GPU0	FWD							BWD

可以看到，在某一时刻仅有1个GPU工作。并且每个timesep花费的时间也比较长，因为GPU需要跑完整个minibatch的前向传播。

GPipe将minibatch划分为4个microbatch，然后依次送入GPU0。GPU0前向传播后，再将结果送入GPU1，以此类推。整个过程如下表

Timestep	0	1	2	3	4	5	6	7	8	9	10	11	12	13
GPU3				F1	F2	F3	F4	B4	B3	B2	B1
GPU2			F1	F2	F3	F4			B4	B3	B2	B1
GPU1		F1	F2	F3	F4					B4	B3	B2	B1
GPU0	F1	F2	F3	F4							B4	B3	B2	B1

F1表示使用当前GPU上的层来对microbatch1进行前向传播。在GPipe的调度中，每个timestep上花费的时间要比朴素层并行更短，因为每个GPU仅需要处理microbatch。

2.2 GPipe的Bubbles问题

bubbles指的是流水线中没有进行任何有效工作的点。这是由于操作之间的依赖导致的。例如，在GPU3执行完F1之前，GPU4只能等待。整个流水线过程中的bubbles如下图所示。

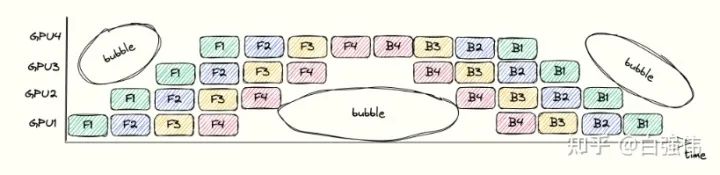
bubbles浪费时间的比例依赖于pipeline的深度  和mincrobatch的数量  。假设单个GPU上完成前向传播或者后向传播的面积为 1 (也就是上图中的单个小方块面积为 1 )。上图中的总长度为 , 宽度为 , 总面积为  。其中, 彩色小方块占用的面积表示GPU执行的时间, 为其  。空白处面积的占比代表了浪费时间的比较, 其值为

 

因此，增大microbatch的数量m，可以降低bubbles的比例。

2.3 GPipe的显存需求

增大batch size就会线性增大需要被缓存激活的显存需求。在GPipe中，GPU需要在前向传播至反向传播这段时间内缓存激活(activations)。以GPU0为例，microbatch1的激活需要从timestep 0保存至timestep 13。

GPipe为了解决显存的问题，使用了gradient checkpointing。该技术不需要缓存所有的激活，而是在反向传播的过程中重新计算激活。这降低了对显存的需求，但是增加了计算代价。

假设所有层都大致相等。每个GPU缓存激活所需要的显存为

 

也就是与单个GPU上的层数以及batch size成正比。相反，使用gradient checkpointing仅需要缓存边界层(需要跨GPU发送结果的层)的输入。这可以降低每个GPU的显存峰值需求

 

 (batchsize) 是缓存边界激活所需要的显存。当对给定的microbatch执行反向传播时, 需要重新计算该microbatch梯度所需要的激活。对于每个GPU上的  层需要  的显存空间。

3. PipeDream

GPipe需要等所有的microbatch前向传播完成后，才会开始反向传播。PipeDream则是当一个microbatch的前向传播完成后，立即进入反向传播阶段。 理论上，反向传播完成后就可以丢弃掉对应microbatch缓存的激活。由于PipeDream的反向传播完成的要比GPipe早，因此也会减少显存的需求。

下图是PipeDream的调度图，4个GPU和8个microbatchs。蓝色的方块表示前向传播，绿色表示反向传播，数字则是microbatch的id。

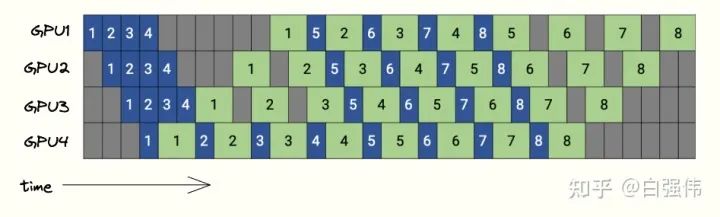
PipeDream在bubbles上与GPipe没有区别，但是由于PipeDream释放显存的时间更早，因此会降低对显存的需求。

4. 合并数据并行和流水线并行

数据并行和流水线并行是正交的，可以同时使用。

• 对于流水线并行。每个GPU需要与下个流水线阶段(前向传播)或者上个流水线阶段(反向传播)进行通信。
• 对于数据并行。每个GPU需要与分配了相同层的GPU进行通信。所有层的副本需要AllReduce对梯度进行平均。

这将在所有GPU上形成子组，并在子组中使用集合通信。任意给定的GPU都会有两部分的通信，一个是包含所有相同层的GPU(数据并行)，另一个与不同层的GPU(流水线并行)。下图是流水线并行度为2且数据并行度为2的示例图，水平方向是完整的一个模型，垂直方向是相同层的不同副本。

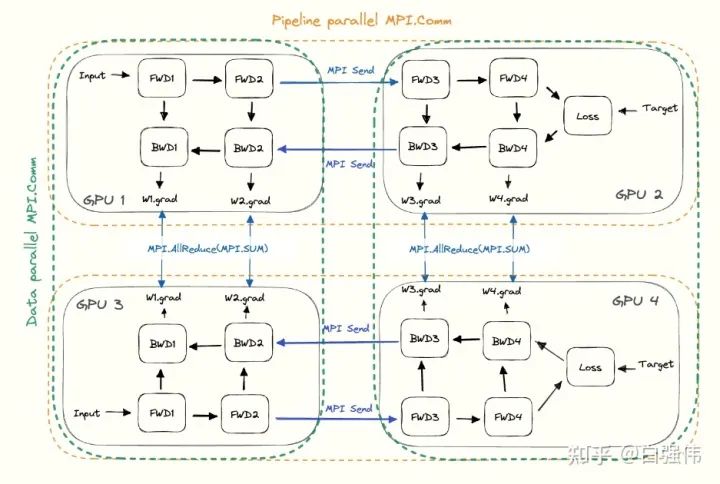
二、张量并行

Transformer中的主要部件是全连接层和注意力机制，其核心都是矩阵乘法。张量并行的核心就是将矩阵乘法进行拆分，从而降低模型对单卡的显存需求。

1. 1D张量并行

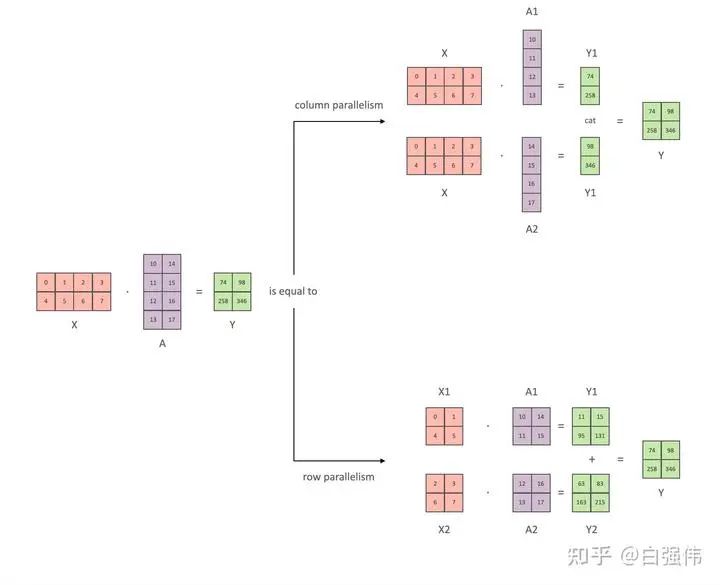
本小节以全链接层  为例, 介绍张量并行。其中,  和  是输入和输出向量,  是权重矩阵,  是非线性激活函数。总量来说张量并行可以分为列并行和行并行(以权重矩阵的分割方式命名), 上图展示了两种并行。

(1) 矩阵乘法角度

这里以矩阵乘法的方式辅助理解1D张量并行。

• 列并行

将矩阵行列划分为n份(不一定必须相等大小)可以表示为  ，那么矩阵乘 法表示为

 

显然，仅需要对权重进行划分。

• 行并行

对权重进行划分，那么必须对输入矩阵也进行划分。假设要将A水平划分为n份，则输入矩阵X必须垂直划分为n份，那么矩阵乘法表示为

 

(2) 激活函数与通信

显然，只观察上面的数据公式，无论是行并行还是列并行 ，都只需要在各个部分计算完后进行一次通常。只不过列并行将通信的结果进行拼接，而行并行则是对通信结果相加。

现在，我们将非线性激活GeLU加上，并模拟两层的全链接层。设X是输入，A和B则是两个全链接层的权重。

 

• 列并行

 

通过上面的公式可以看到。当我们将A和B提前划分好后，就可以独立进行计算，在计算出后再进行通信。也就是说，这个例子中虽然有两个全链接层，但是仅需要在得到最终结果前进行通信即可。

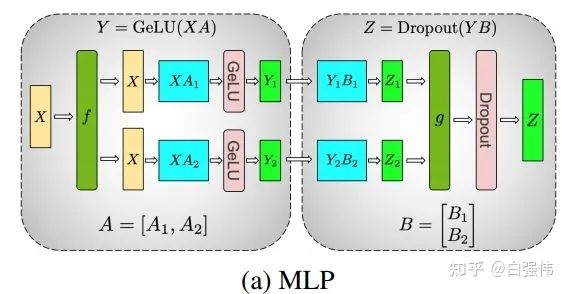
所以，多个全链接层堆叠时，仅需要在最终输出时进行一次通信即可(如上图所示) 。

• 行并行

 

由于  是非线性的，所以

 

因此，行并行每一个全链接层都需要进行通信来聚合最终的结果。

(3) 多头注意力并行

多头注意力并行不是1D张量并行，但是由于其是Megatron-LM中与1D张量并行同时提出的，所以这里也进行简单的介绍。

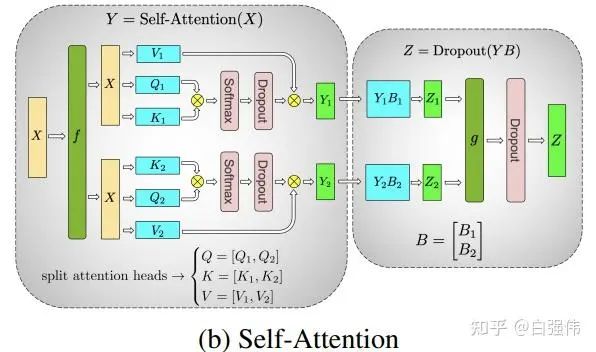
由于多头注意力的各个头之间本质上就是独立的，因此各个头完全可以并行运算。

注意：张量并行(TP)需要非常快的网络，因此不建议跨多个节点进行张量并行。实际中，若一个节点有4个GPU，最高的张量并行度为4。

2. 2D、2.5D张量并行

在1D张量并行后，又逐步提出了2D、2.5D和3D张量并行。这里对2D和2.5D张量并行进行简单介绍：

(1) 2D张量并行

1D张量并行并没有对激活(activations，也就是模型中间层的输出结果)进行划分，导致消耗大量的显存。

这里仍然以矩阵乘法  为例, 给定有  个处理器。这里假设 , 则将X和A都划分为  的块。

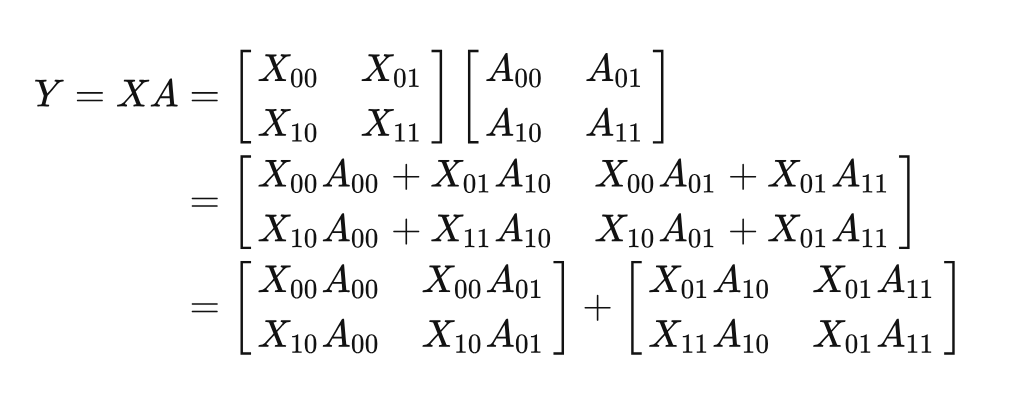
基于上面的矩阵乘法的变化，可以发现Y=XA可以分解为两个矩阵相加。具体来说，两个矩阵的结果仍然需要串行的计算。但是，单个矩阵中的4个子矩阵可以使用  的处理器来并行计算。

当 , 也就是第一步。对

 

进行广播, 所有  的处理器均拥有这 4 个子矩阵。然后分别执行  。经过这一步后就得到了第一个矩阵的结果。

当  。对

 

进行广播，各个处理器在分别计算。最终得到第二个矩阵的结果。

将两个矩阵的结果相加。

(2) 2.5D张量并行

仍然是矩阵乘法 , 并假设有  个处理器, 将 X划分为  行和  列。不妨设 , 将  和  分别划分为

 

那么有

 

 

其中， concat 表示两个矩阵的垂直拼接操作。

基于上面的推导, 可以发现被拼接的两个矩阵天然可以并行计算。即 和  可以并行计算。看到这里, 应该就可以发现这两个矩阵乘法就是上面的2D张量并行适用的形式。所以, 我们总计有  个处理器, 每  个处理器使用2D张量并行来处理对应的矩阵乘法。最后, 将两个2D张量并行的结果进行拼接即可。

三、3D并行

总的来说，3D并行是由数据并行(DP)、张量并行(TP)和流水线并行(PP)组成。前面已经分别介绍了TP和PP，ZeRO-DP是一种显存高效的数据并行策略，原理见文章：

白强伟：【深度学习】【分布式训练】DeepSpeed：AllReduce与ZeRO-DP142

https://zhuanlan.zhihu.com/p/610587671

下面介绍如何将三种并行技术结合在一起，形成3D并行技术。

1. 一个3D并行的例子

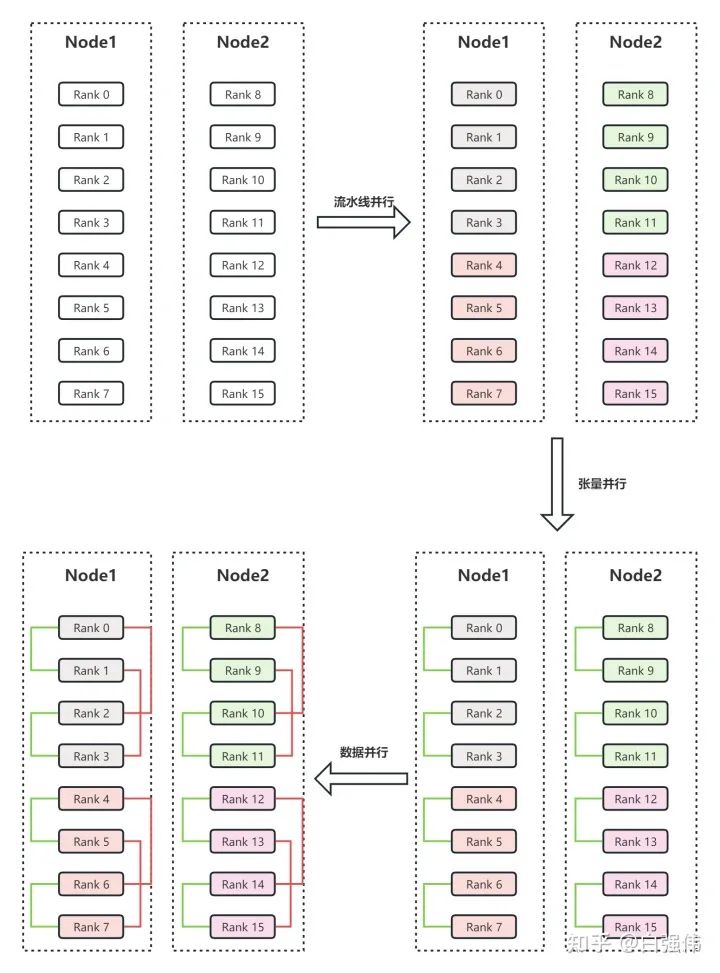
假设有两个节点Node1和Node2，每个节点有8个GPU，共计16个GPU。16个GPU的编号分别为Rank0、Rank1、...、Rank15。此外，假设用户设置流水线并行度为4，张量并行度为2。

流水线并行。流水线并行会将整个模型划分为4份，这里称为sub_model_1至sub_model_4。每连续的4张GPU负责一个sub_model。即上图右上角中，相同颜色的GPU负责相同的sub_model。

张量并行。张量并行会针对流水线并行中的sub_model来进行张量的拆分。即Rank0和Rank1负责一份sub_model_1，Rank2和Rank3负责另一份sub_model_1；Rank4和Rank5负责sub_model_2，Rank6和Rank7负责另一份sub_model_2；以此类推。上图右下角中，绿色线条表示单个张量并行组，每个张量并行组都共同负责某个具体的sub_model。

数据并行。数据并行的目的是要保证并行中的相同模型参数读取相同的数据。经过流水线并行和张量并行后，Rank0和Rank2负责相同的模型参数，所以Rank0和Rank2是同一个数据并行组。上图左上角中的红色线条表示数据并行组。

2. 3D并行分析

为什么3D并行需要按上面的方式划分GPU呢？ 首先，模型并行是三种策略中通信开销最大的，所以优先将模型并行组放置在一个节点中，以利用较大的节点内带宽。其次，流水线并行通信量最低，因此在不同节点之间调度流水线，这将不受通信带宽的限制。最后，若张量并行没有跨节点，则数据并行也不需要跨节点；否则数据并行组也需要跨节点。

流水线并行和张量并行减少了单个显卡的显存消耗，提高了显存效率。但是，模型划分的太多会增加通信开销，从而降低计算效率。ZeRO-DP不仅能够通过将优化器状态进行划分来改善显存效率，而且还不会显著的增加通信开销。