电机绕组的磁势讲解

绕组是电和磁的桥梁。匝链绕组的磁链发生变化时，绕组中就会产生感应电势；给绕组通以电流时，就会产生磁势。关于电机绕组的感应电势相关内容，在前面几期中已经详细论述，本期开始讲电机绕组的磁势。

由于整数槽绕组的磁势分布比较简单，分数槽绕组的磁势分布比较复杂。本着由浅入深、由简到繁的原则，首先分析整数槽绕组的磁势，再分析分数槽绕组的磁势。在分析整数槽绕组的磁势时，首先从单个整距线圈的磁势入手，进而分析多个整距线圈组的磁势和短距线圈组的磁势，从而得出单相绕组的磁势，最终得出三相绕组的合成磁势以及绕组磁势的谐波。分析完三相整数槽绕组和分数槽绕组的磁势，最后讨论多相(相数m＞3)绕组的磁势以及变极调速的原理。由于内容较多，我们将分多期进行讲解。本期主要讲单相整数槽绕组的磁势。为了分析简化，做以下假设：①假设槽内电流集中在槽中心处；②假设铁心的磁导率为无穷大，所有磁势都降落在气隙中。

1 单个整距线圈的磁势

绕组都是由许多个线圈连接而成，要想分析绕组的磁势，必须从单个线圈的磁势入手。如图1a为一台两极电机的示意图，定子中只有一个整距线圈，设整距线圈的匝数(每槽导体数)为Nc。

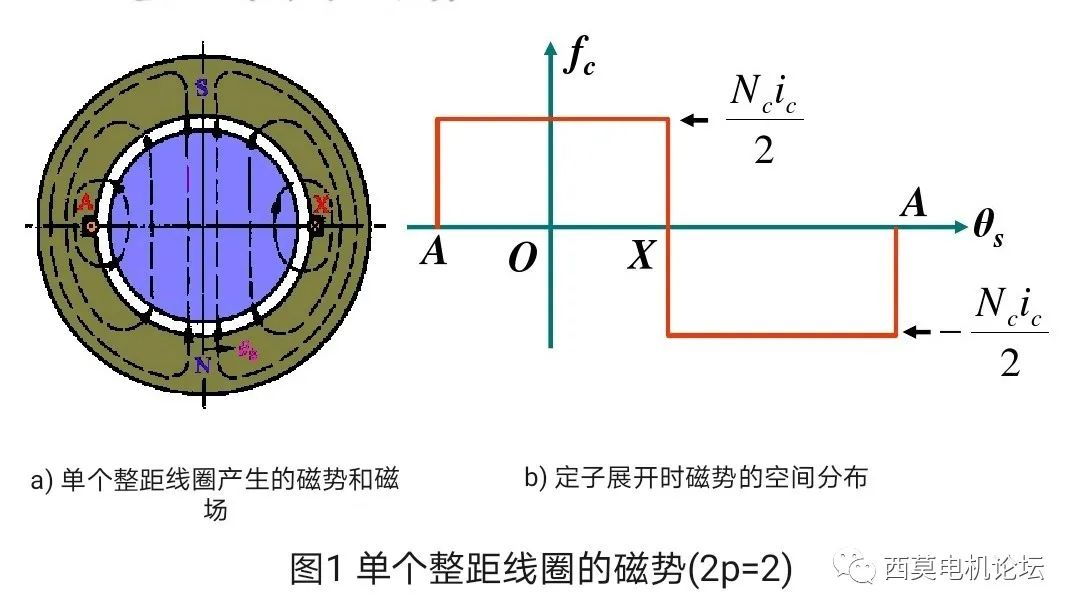
当线圈中通以交流电流ic时，例如某一时刻从X流入，从A流出，则这个线圈产生的磁势即为其安匝数Nc•ic，在该磁势作用下，线圈将产生一个两极磁场，如图1a)所示，定子内圆下端为N极，上端为S极。由于整距线圈相对于线圈轴线对称，且相对于线圈平面上下也是对称的，因此在假设铁心的磁导率为无穷大的情况下，该磁势被平均分配到上下半部分气隙中，每个气隙得到的磁势即为总磁势的一半，即Nc•ic/2，定义N极磁势为正，S极磁势为负，若以线圈的轴线处为原点，将气隙圆周展开，即得到图1b)所示的磁势分布。由图可见，由于假设槽内电流集中在槽中心处，则磁势在经过一个线圈边时将发生Nc•ic的跳变，因此一个整距线圈的磁势沿气隙在空间的分布是一个矩形波，矩形波的幅值为Nc•ic/2。该磁势的空间分布表达式为：

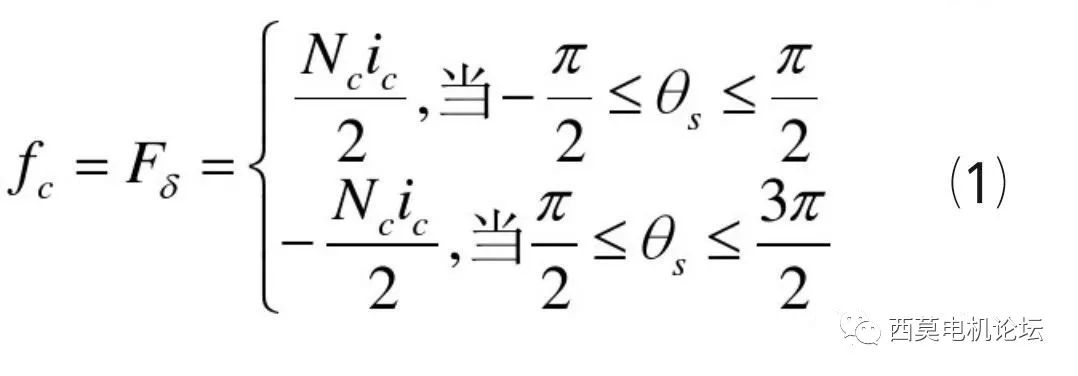
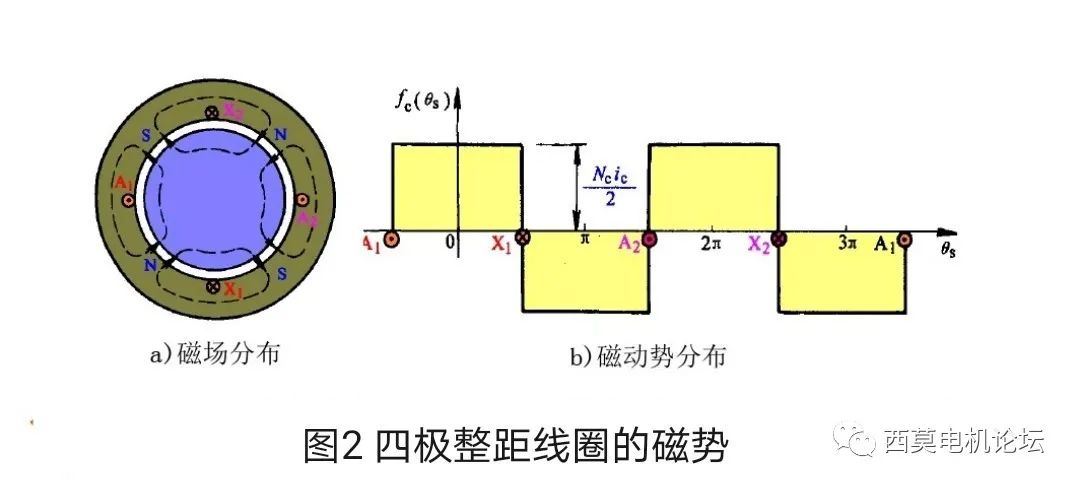
以上分析的是一对极的情况，对于整数槽多极电机，由于各对极下的磁势分布情况均为一对极的重复，因此只需分析一对极即可，此时多极整距线圈产生的磁势在空间的分布仍为矩形波，矩形波的幅值仍为Nc•ic/2，只不过是波长(2τ)不是两极电机那样为整个气隙圆周周长，而是变为了1/p的气隙周长。如图2所示为四极整距线圈的磁场和磁势分布情况。

如果线圈内所通的电流为直流电流，则矩形波的幅值就是Nc•ic/2固定不变的；若线圈内所通的电流为随时间按余弦规律变化的交流电流，即：

ic=2^½•Ic•cosωt (2)

则单个整距线圈产生的磁势在空间上的分布仍然是矩形波，但矩形波的幅值则随时间按余弦规律变化，即矩形波的幅值为：

fc(t)=Fcm•cosωt (3)

其中矩形波幅值的最大值为：

Fcm=(1/2^½)•Ic•Nc (4)

式中：Ic为线圈内交流电流的有效值。

当线圈内电流达到最大值2^½•Ic时，矩形波磁势幅值达到最大值Fcm；随着电流瞬时值的减小，磁势的幅值也将随之减小，当电流减小到0时，整个空间的磁势也变为0；当电流变为负值时，磁势也随之改变方向，电流达到负的最大值-2^½•Ic时，矩形波磁势幅值也达到负的最大值-Fcm。这种从空间上看，轴线位置固定不动，从时间上看，其大小不断地随着电流的交变而在正、负最大值之间脉振变化的磁势(磁场)，叫做“脉振磁势(磁场)”，物理上也称为“驻波”。脉振的频率显然与交流电流的频率相同。

这里特别要重复强调的是，一定要把磁势的空间分布规律和随时间变化的规律区别清楚。空间分布用空间位置角度θ的函数来表达，整距线圈磁势的空间分布是一个矩形波，若线圈内所通电流不变，则矩形波的幅值也不变，表达式见式⑴；磁势随时间变化的规律用时间t的函数来表示，若线圈中的电流随时间按余弦规律变化，则沿定子内圆分布的矩形磁势波幅值大小也将随时间按余弦规律变化，其表达式如式⑶所示。

为了便于分析计算，常用谐波分析法对这个矩形波沿空间进行傅立叶分解，再次强调是沿空间进行傅立叶分解！得到矩形波沿空间的基波和各次谐波。如图3所示。

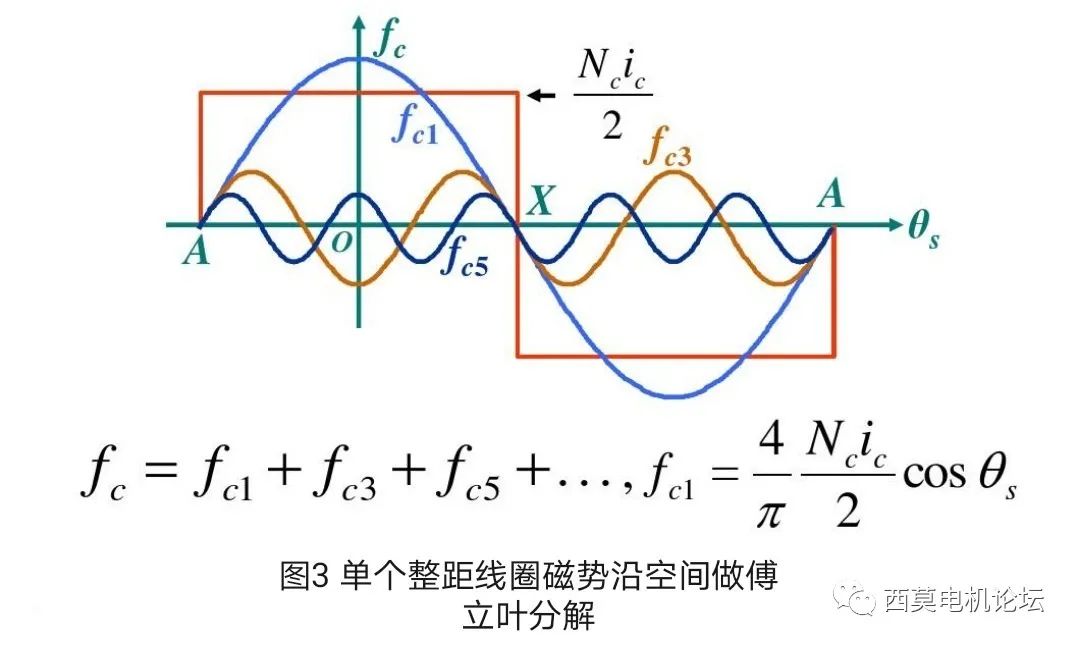
由图3可见，由于整距线圈产生的矩形波磁势是一个奇谐函数，因此将其做傅立叶分解后，只含有奇次谐波，而不含有偶次谐波。分解后磁势表达式为：

fc(θ,t)=fc1•cosθ+fc3•cos3θ+fc5•cos5θ+fc7•cos7θ+… (5)

其中基波磁势的极对数为p，基波磁势的幅值为：

fc1=(4/π)Fcm•cosωt=Fcm1•cosωt (6)

υ次谐波磁势的极对数为υp，幅值为：

fcυ=±(1/υ)•Fcm1•cosωt=±Fcmυ•cosωt (7)

上式中：Fcm1=(4/π)Fcm，为基波磁势幅值的最大值；Fcmυ=(1/υ)Fcm1，为υ次谐波磁势幅值的最大值；当υ=4k+1时取“+”号，当υ=4k-1时取“-”号，k=1,2,3…。

综合以上各式，得单个整距线圈产生的磁势时空表达式为：

fc(θ,t)=Fcm1•cosθ•cosωt

-(1/3)•Fcm1•cos3θ•cosωt

+(1/5)•Fcm1•cos5θ•cosωt

-(1/7)•Fcm1•cos7θ•cosωt

=Fcm1•[cosθ-(1/3)cos3θ+(1/5)cos5θ-(1/7)cos7θ+…]•cosωt (8)

由⑻式可以得到以下结论：

①单个整距线圈通以余弦(正弦)交流电流时，会产生一个脉振磁势，它既是空间θ的函数又是时间t的函数。即这个脉振磁势是沿空间相对于线圈轴线对称的矩形波，矩形波的幅值大小又随时间t按余弦(正弦)规律变化，变化频率与电流频率相等。

②把这个矩形波磁势沿空间做傅立叶分解后，只含有奇次谐波，谐波磁势幅值的大小与谐波次数成反比，谐波次数越高，幅值越小。

③基波和谐波的波峰(波谷)在线圈的轴线位置，取“+”号时为波峰；取“-”号时为波谷。

2 整距分布绕组的基波磁势

几个线圈串联组成一个线圈组，也称极相组。线圈组的磁势应该就是各单个线圈磁势的叠加。由于各线圈分布在气隙圆周上，相邻线圈之间在空间上错开了一定的角度α(通常是槽距角)，因此各线圈磁势的叠加应该是矢量的叠加。如图4所示为一个由q=3的整距线圈组成的极相组，极相组的三个线圈依次分布在三个相邻的槽内，所以称此绕组为整距分布绕组。

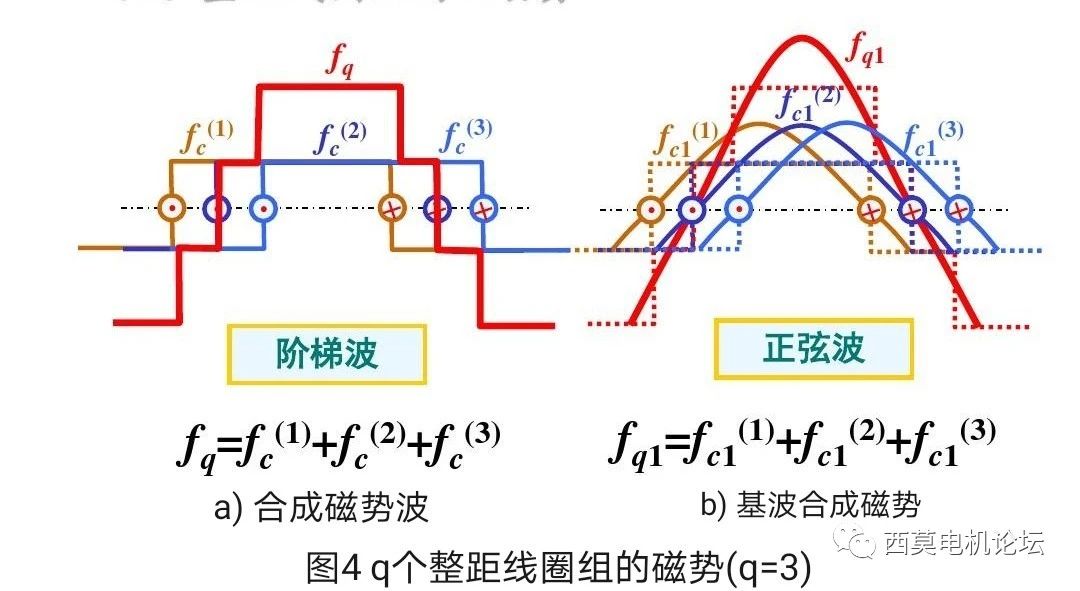
每个整距线圈产生的磁势都是一个矩形波。由于每个整距线圈的匝数相等，且由于各线圈串联，通过的电流也相等，故各线圈的矩形波磁势幅值相等；由于线圈是分布的，相邻线圈在空间上间隔α角，所以各线圈的矩形波磁势在空间上亦相隔α电角度。把这三个线圈分别产生的矩形波磁势逐点相加，即可得到整个极相组的磁势波，如图4a)所示。由图可见极相组的合成磁势为一个阶梯波。将各单个整距线圈产生的矩形波磁势做空间傅立叶分解，得到各单个线圈磁势的基波和一系列高次谐波。这里我们先分析磁势基波，磁势谐波将在后续分析。图4b)即为三个整距线圈的基波磁势，其幅值相等、空间各相差α电角度。将这三个线圈的基波磁势逐点相加，即可得到整个极相组的合成基波磁势。由于基波磁势在空间按余弦规律分布，故可以用空间矢量表示和运算，于是q个线圈的基波合成磁势矢量就等于各线圈基波磁势矢量的矢量和，如图5所示。

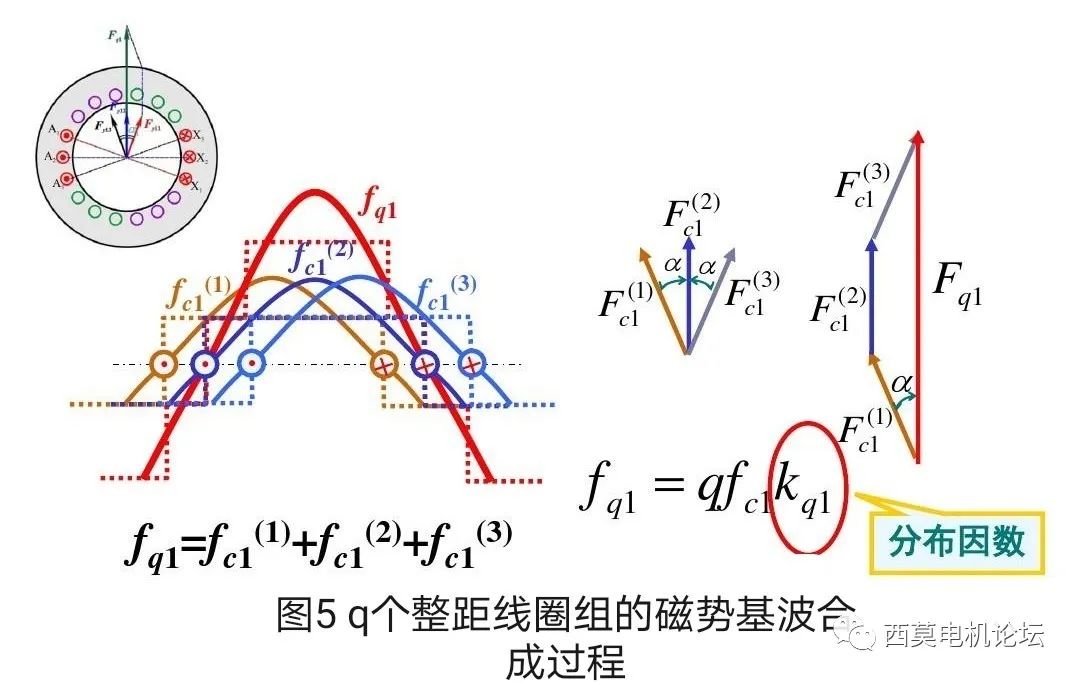
由图5不难看出，利用矢量运算时，分布线圈基波磁势的合成与前面所讲的基波电势的合成完全相似，因此同样可以引入分布系数(或分布因数)Kd1来计及线圈分布的影响，即q个分布线圈产生的合成基波磁势等于直接将q个线圈的基波磁势算术相加基础上，打一个分布因数Kd1的折扣。于是q个整距分布线圈组成的极相组的合成磁势基波为：

fq1(θ,t)=q•fc1•Kd1•cosθ

=(4/π)•(1/2^½)•Ic•q•Nc•Kd1•cosθ•cosωt (9)

3 短距分布绕组的基波磁势

以上分析了整距线圈及整距分布绕组的基波磁势，接下来分析短距分布绕组的基波磁势。如图6所示为q=2、线圈节距y1=5(极距τ=6)的双层短距分布绕组，一对极下属于同一相有两个极相组。按照短距绕组的连接规律，应该是第1、2槽上层边分别与第6、7槽下层边连接构成一个极相组；第7、8槽上层边分别与12、13槽的下层边连接构成另一个极相组。由于在铁心有效长度内，磁势的大小和波形仅仅取决于槽内有效边的分布情况以及导体内的电流，而与线圈端部的连接次序无关，因此，为了简化分析，可以把两个短距极相组的上层边视为一组q=2的整距分布绕组；把两个短距极相组的下层边视为另一组q=2的整距分布绕组；这两组整距分布绕组在空间上错开ε电角度。这样得到的磁势分布与两个短距分布绕组的磁势分布是完全一样的。其中ε角恰好等于短距线圈的节距比整距时缩短的电角度，即ε=180º•(τ-y1)/τ。

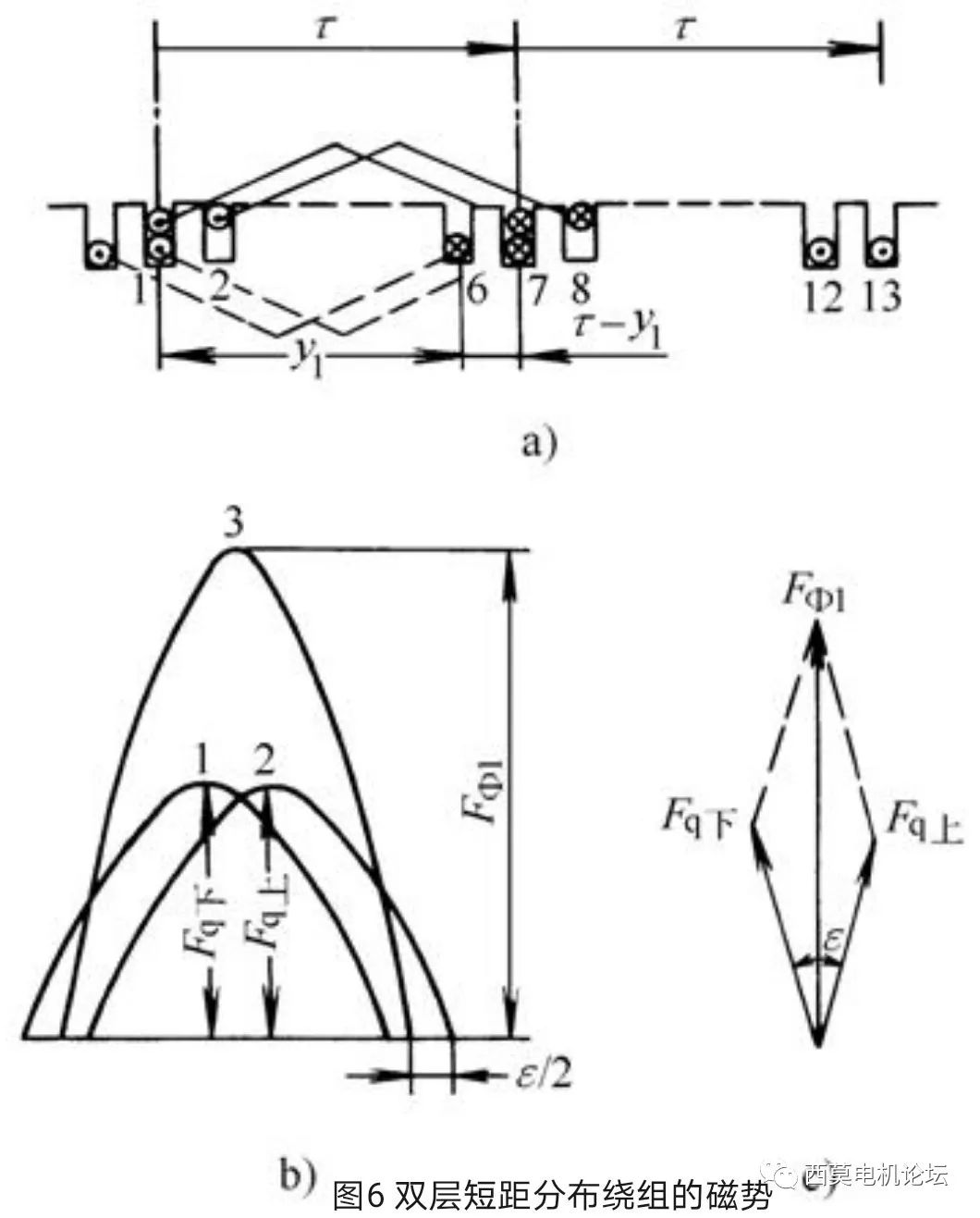
图6b)表示两条分别代表上下层整距分布绕组基波磁势的正弦曲线逐点相加，得到双层短距分布绕组的基波磁势；图6c)为对应的基波磁势空间矢量相加过程。不难看出，双层短距分布绕组的基波磁势是双层整距时的cos(ε/2)倍，而这个系数cos(ε/2)=sin(90º•y1/τ)=Kp1，也就是说，计及短距时，绕组的磁势基波引入的系数恰恰是计算短距绕组电势基波时引入的短距系数。于是，双层短距分布绕组的基波磁势为：

fq1(θ,t)=2q•fc1•Kd1•Kp1•cosθ

=(4/π)•2^½•Ic•q•Nc•Kdp1•cosθ•cosωt (10)

其中：Kdp1=Kd1•Kp1为基波绕组系数，与电势的基波绕组系数相同。

4 单相绕组的基波磁势

由于各对极下的磁势和磁阻组成一个对称的分支磁路，因此一相绕组产生的磁势就等于一对极下的磁势，也就是⑽式所示的磁势也就是单相绕组的磁势。考虑到⑽式中的电流Ic为极相组中导体内的电流有效值；Nc为极相组中每个线圈的匝数(对于单层绕组为每槽导体数；对于双层绕组为每半槽导体数)，而单相绕组的磁势应该体现与相电流和每相串联匝数的关系。因此需要将⑽式中的电流IC和线圈匝数分别用相电流和每相串联匝数予以替换。由于双层绕组的每相串联匝数W=q•2p•Nc/a，其中a为并联支路数；相电流IΦ=a•Ic，将此关系代入⑽式，得每相绕组的基波磁势为：

fΦ1(θ,t)=(4/π)•2^½•(W•Kdp1/2p)•IΦ•cosθ•cosωt=FΦ1•cosθ•cosωt (11)

其中FΦ1为单相绕组的基波磁势幅值。

FΦ1=(4/π)•2^½•(W•Kdp1/2p)•IΦ=0.9•(W•Kdp1/p)•IΦ (12)

以上两式中：W为每相串联匝数，IΦ为相电流有效值。需要说明一下，虽然以上两式是在双层绕组基础上推导出来的，但无论是单层绕组还是双层绕组，以上两式都适用。

由以上两式可知：

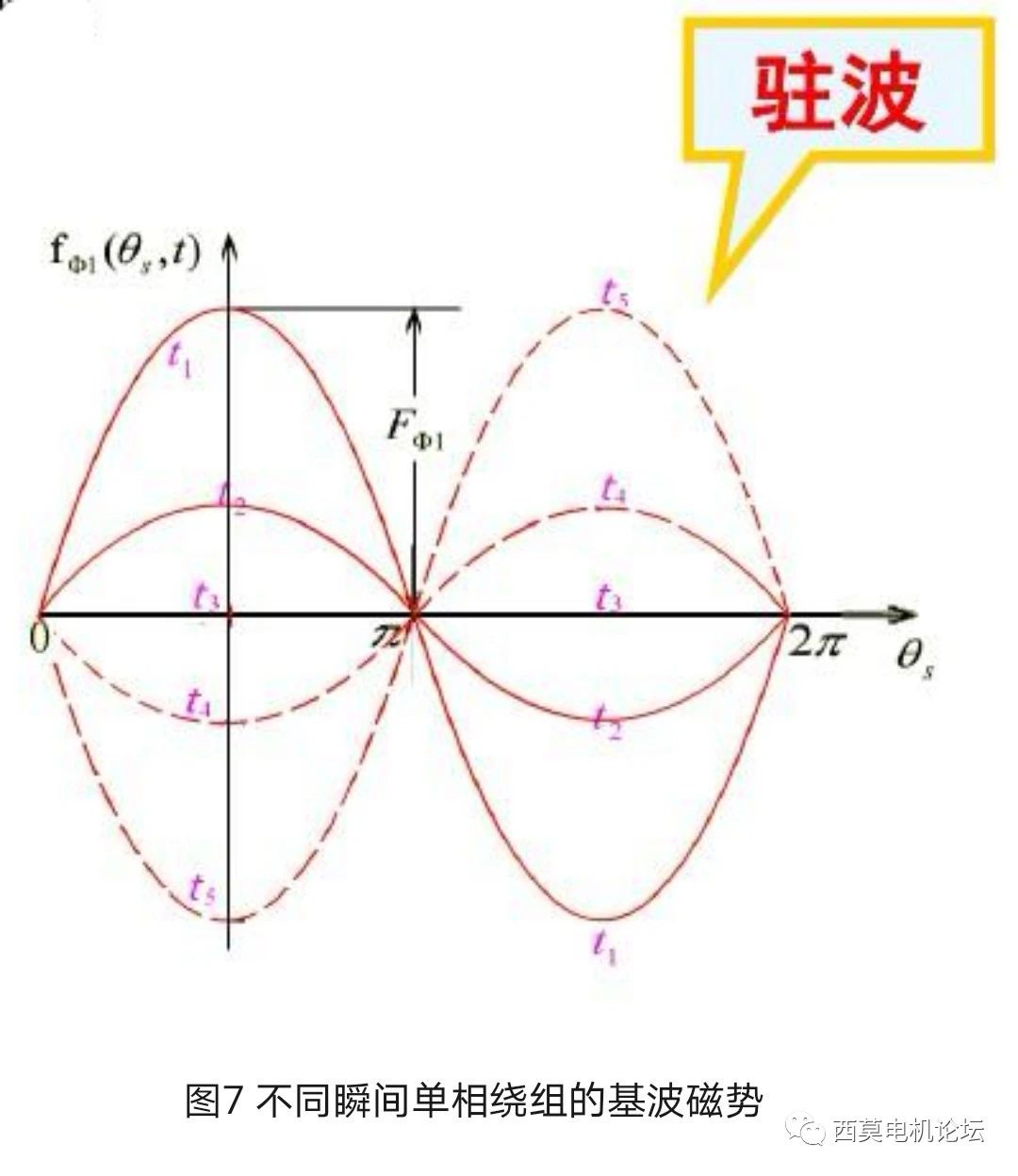
①当单相绕组中通以余弦(正弦)交流电流时，产生的基波磁势为脉振磁势，即在空间上随位置角θ按余弦规律分布，在时间上随ωt按余弦(正弦)规律脉振，而空间分布的轴线固定不动。如前所述，这种从空间上看轴线固定不动，从时间上看其瞬时值不断地随电流的交变而在正、负幅值之间脉振的磁势(磁场)即称为脉振磁势(磁场)，物理上称为驻波。脉振的频率取决于电流的频率。如图7所示，为单相绕组在不同瞬间的基波磁势波。

②基波磁势的幅值正比于每对极每相的有效串联匝数W•Kdp1/p和相电流IΦ。

5 单相绕组的谐波磁势

线圈产生的矩形波磁势中除了基波磁势外，还有一系列高次谐波。对于整数槽绕组，这些谐波中只含有奇次谐波，而不含有偶次谐波。按照上述基波磁势的合成推导方法，可推导出单相绕组的υ次谐波分量为：

fΦυ(θ,t)=±(1/υ)•(4/π)•2^½•(W•Kdpυ/2p)•IΦ•cos(υθ)•cosωt=±FΦυ•cos(υθ)•cosωt (13)

其中：

FΦυ=(1/υ)•(4/π)•2^½•(W•Kdpυ/2p)•IΦ

=(1/υ)•0.9•(W•Kdpυ/p)•IΦ

=(1/υ)•(Kdpυ/Kdp1)•FΦ1 (14)

以上两式中Kdpυ为υ次谐波绕组系数。

以上两式可见，单相绕组产生的谐波磁势仍然是一个脉振磁势，从空间上看按υ次谐波分布，波长是基波的1/υ，某一条谐波空间分布轴线(即波峰和波谷的位置)也与基波磁势重合；从时间上看仍按ωt的余弦规律脉振，脉振频率与基波相同，谐波磁势的幅值与谐波次数成反比，与谐波绕组系数成正比，谐波次数越高，谐波幅值越小。另外可以通过减小谐波绕组系数的方法来削弱谐波磁势。

本期介绍了单相绕组产生的磁势，推导过程比较复杂，如实在没有耐心，可以跳过推导部分，但需要记住文中的一些重要结论。简单归纳一下就是：单相绕组通以正弦交流电流时产生的磁势是一个脉振磁势，脉振频率与电流频率相同，在空间分布上包括基波和一系列高次(奇次)谐波，基波和高次谐波的峰(谷)值位置与绕组的轴线重合。必须强调一点，上述结论只适用于整数槽绕组，分数槽绕组某些结论不适用，关于分数槽绕组的磁势还会在以后的文章中详述。

　　审核编辑：汤梓红