详细讲解傅里叶变换

文章来源：力学科普

原文作者：Lee

提到傅里叶变换，你是不是又想起了大学课程里被它支配的恐惧。其实，傅里叶分析不仅仅是一个数学工具，更是一种可以彻底颠覆一个人以前世界观的思维模式。如果用方程写一部科学史，傅里叶变换必然拥有位置，它的应用之广，可以处理图片，也可以解读星空，可以帮忙建造不易倒塌的房子，也可以深度参与金融数据分析。无论是混杂的信号，还是复杂的卷积，都可以被它的魔法驯服，变得清晰明了、简洁高效。那么，傅里叶变换是如何做到对万物进行拆解的呢？

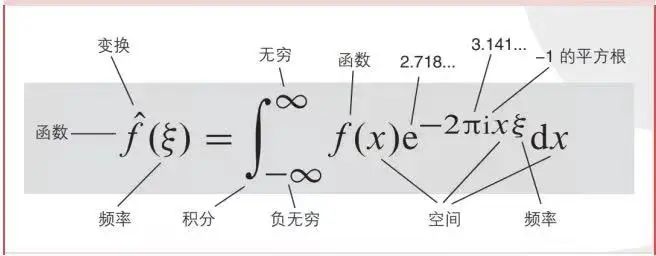
傅里叶变换最精彩之处就是能够将信号在时域与频域之间进行变换，因此我们先解释一下什么是时域和频域。所谓时域是描述数学函数或物理信号对时间的关系，从我们出生，我们看到的世界都以时间贯穿，股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而频域则描述了信号的频率结构及频率与该频率信号幅度的关系，从这个视角来观察世界你会发现世界是永恒不变的。这就好比在时域视角下我们观察到钢琴的琴弦一会上一会下的摆动，就如同一支股票的走势；而在频域视角则是永恒的音符。

简单来说，傅里叶级数贯穿了时域与频域，将任何形式的周期性信号无限拆解，分为多个有规律的简单正弦波信号。而对于任何非周期性信号则可以看做是超大号的周期信号，作为傅里叶级数的延展，傅里叶变换可以将任何复杂的的非周期性信号规律性拆解。这就好比当我们去买菜的时候，各种蔬菜都不一样，但都能转换成“n个1斤砝码+m个1两砝码”的组合。

从现代数学的眼光来看，傅里叶变换是一种特殊的积分变换。它能将满足一定条件的某个函数表示成正弦基函数的线性组合或者积分。在不同的研究领域，傅里叶变换具有多种不同的变体形式，如连续傅里叶变换和离散傅里叶变换。

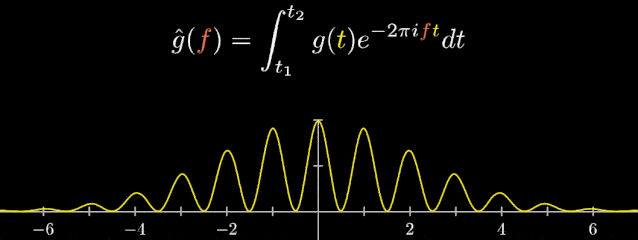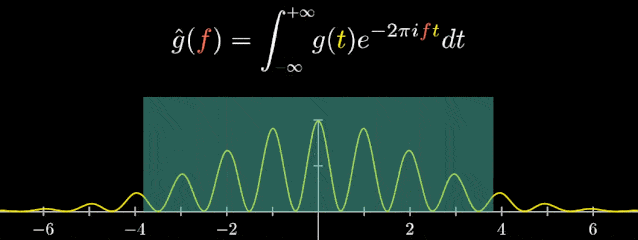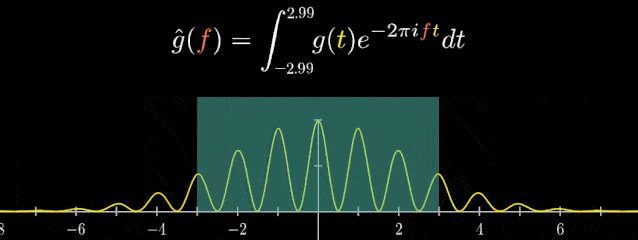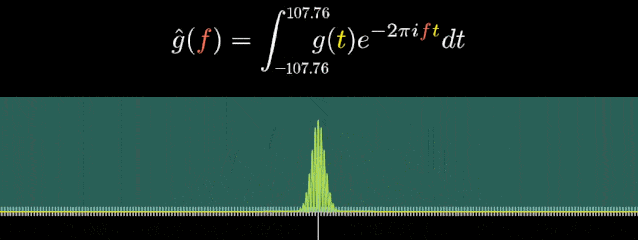
“傅里叶变换”最初被运用于热力学分析中，随着时代与科技的发展，它们也以各种方式被广泛应用于医学、声学、密码学、概率论、海洋学、计算机科学、量子力学等各个领域，下面举一些傅里叶变换应用的实例。

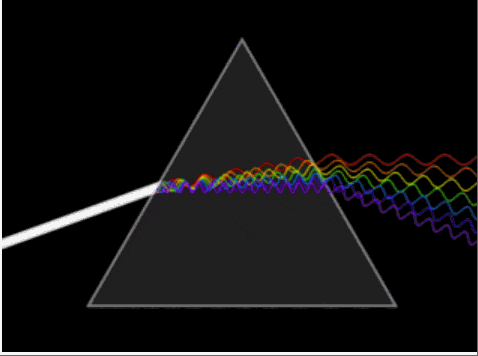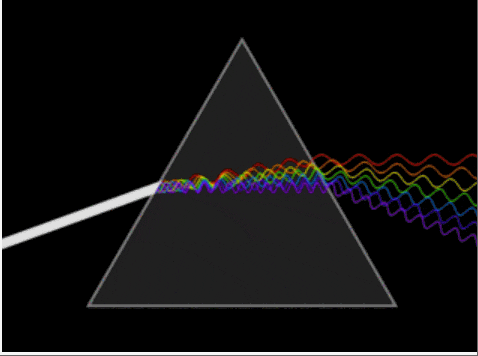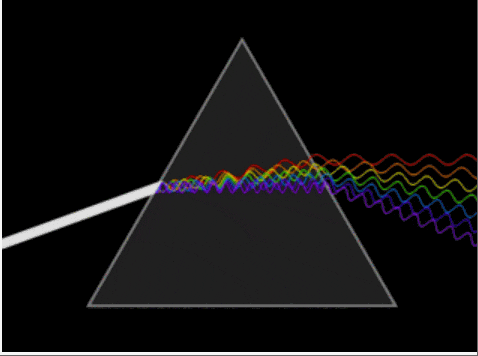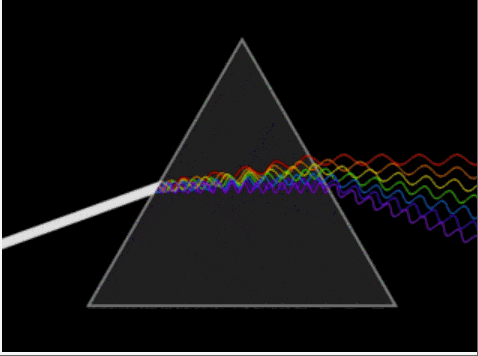
冈萨雷斯在《数字图像处理》一书中，将傅里叶变换比作一个玻璃棱镜。棱镜可以将光分解为不同颜色，颜色由波长（或频率）来决定。傅里叶变换可以看作是数学上的棱镜，将函数基于频率分解为不同的成分。我们日常用美颜相机进行磨皮、美化操作的基本原理便是通过傅里叶变换，经过一定的处理，减少或增添某些频率的幅度，达到让图像变得更模糊或更鲜亮的目的。

其实人类大脑本身就具有“傅里叶变换”的功能。例如，我们可以从一段嘈杂的公园环境音里分辨出男声、女声、老人、儿童、狗叫声、脚步声、水流声和噪声，下面这张图形象地展示了这一过程，左边的是你听到的声音，而右边的图则是你的大脑经过傅里叶变换，分析出了十几种不同的发声物体。市面上的变声软件，大叔嗓秒变萝莉音的基本原理也是这样，把一段音频，分离出男声和女声，将男声改为女声的频率，然后还原回去，实现男声变女声。

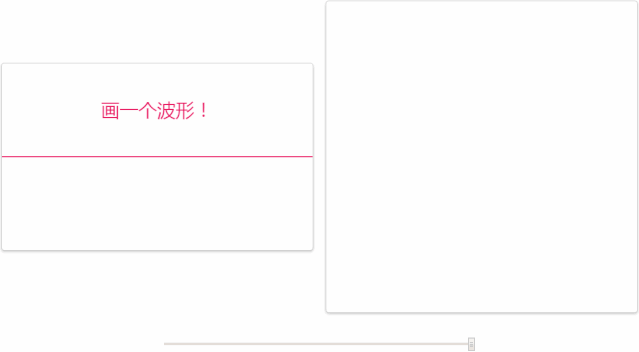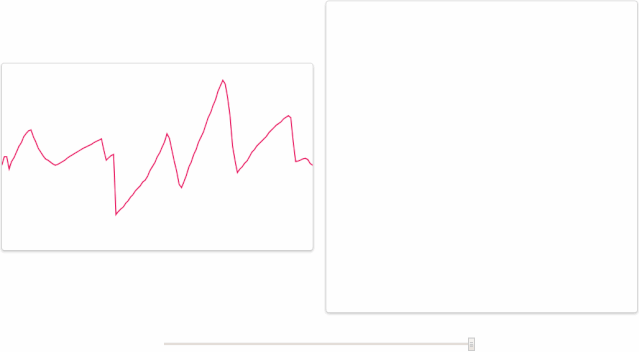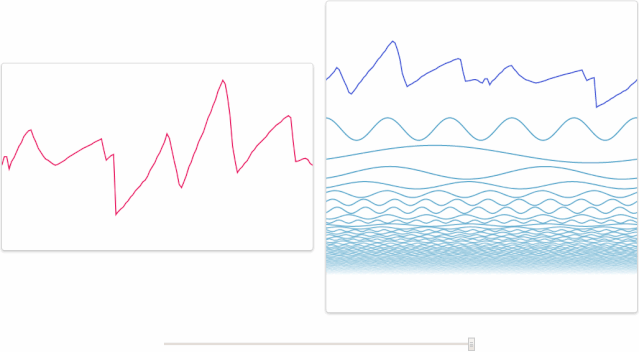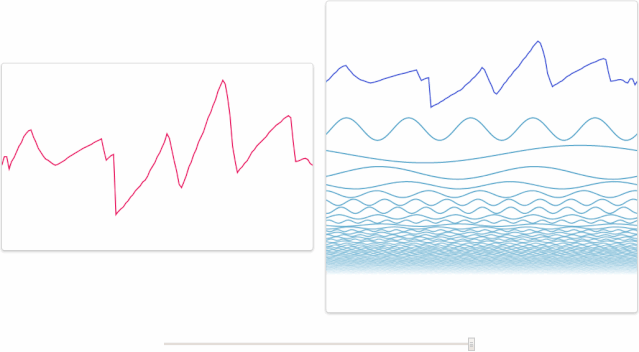
再比如，MP3文件格式正是基于这个原理运行的——为了节省空间，它把几乎察觉不到的频率部分舍弃掉了。只保留确定重要的频率成分，丢弃那些不重要的部分，以(相当准确地)表现原始的音轨。尽管得出的波形与原始波形不一样，但是听起来将会和原始声音很接近。

审核编辑：汤梓红