MATLAB在追迹光线计算中的应用

摘要 ：给出了理想光具组系统矩阵的MATLAB计算程序，并借助MATLAB进行光线追迹与数值拟合，得到了像差(球差)的多项式及曲线图。

0.引 言

几何光学把光源或物体看成是由许多几何点组成，并把由这种点发出的光抽象成几何线一样的光线，那么，只要讨论光线的传播来研究这种点经光学系统的成像，问题就变得非常简便和实用。尽管几何光学所研究的只是一种对真实情况的近似处理方法，按此方法所解决的有关光学系统的成像分析、计算和设计等方面的光学技术问题，在大多数场合下与实际情况相符。所以，几何光学有很大的实用意义，是研究光学仪器理论必不可少的基础。MATLAB作为一款优秀的数学软件，集成了最优秀的算法，除具有强大的矩阵计算功能和友好的界面，还具备了良好的可视化性能．这些特点使得 MU蛆在光线计算、像差分析中大显身手。

1.理想光具组的矩阵计算

几何光学定律只在一级近似条件(sinφ≈φ)下成立，根据费马定理在近轴条件下推出的物象方程，进而得到牛顿公式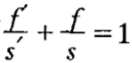（），高斯公式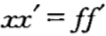（）以及光焦度公式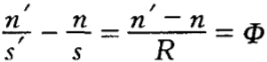（），使得宏观光 学的问题基本解决。对于较复杂的光学系统，可以通 过追迹光线，根据物象相对性原理及逐个球面成像法，求出物体经整个系统后所成的像。由于近轴物象空间的光线状态的变化可以描述成某种线性关系，因此，用矩阵方法处理许多折射面组成的复杂光学系统尤其便利，只要追随光线写下光线的传递矩阵及折射矩阵，再依次相乘，就可求出光学系统的基点和基面，也可得到物象关系。见表1

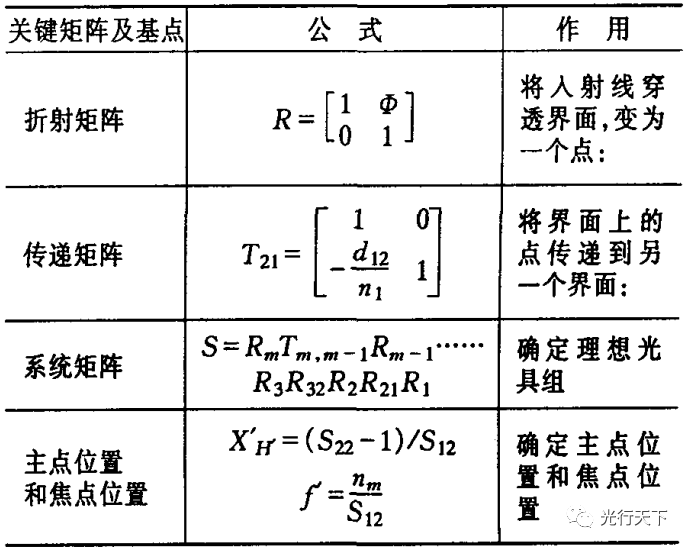
下面，以双胶合望远镜的目镜为例(如图1所示)，

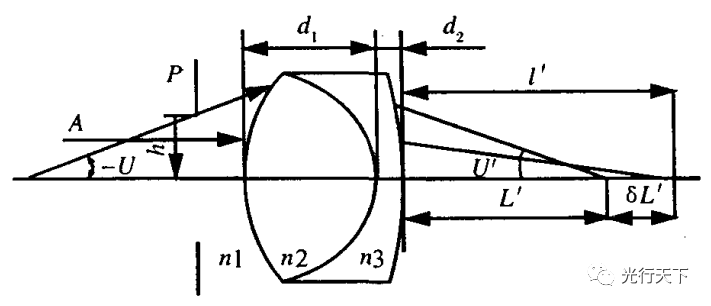
图1.双胶合透镜目镜球差示意光路图

作有关系统矩阵的计算，rl=62.5，r2=-43.65，

r3=-124.35，nl=1，n2=1.51633，n3=1.6727，dl=4.0，d2=2.5，入射孔径半径a=10。

通过MATLAB编写的程序，很容易得到S矩阵=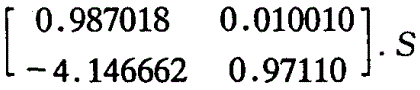矩阵计算程序流程如图2所示。

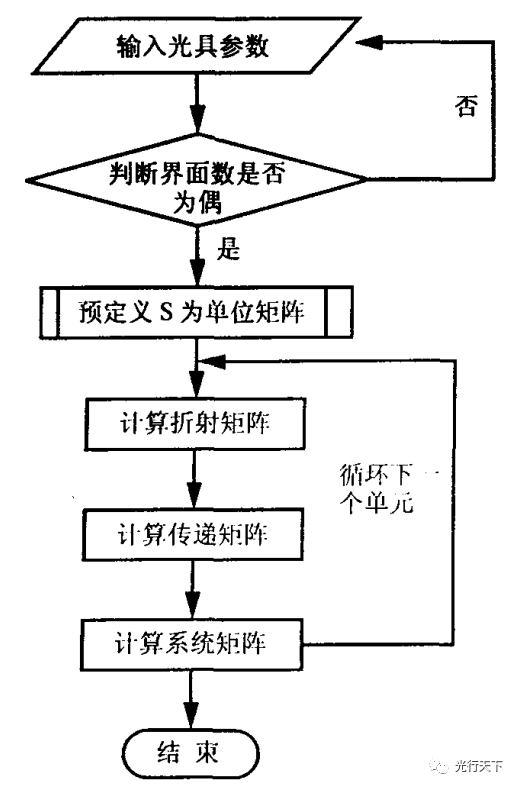
图2. 系统矩阵计算程序流程图

2.像差分析及可视化

我们已经知道，任何实际光学系统只要在近轴区，就能象理想光具系统那样具完善成像的性质。因此，即使单个透镜，只要其相对孔径(孔径僬距)和视场很小，也是能够以单色光成完善像。但是，遗憾的是，只能对近轴小物体以细光束成完善像的光学系统并无实际意义，因为恰恰是相对孔径和视场这两个参数与光学系统的功能和使用价值密切相关。实际上，任何光学系统都需根据仪器的要求而具一定大小的视场和孔径，它远远超出近轴区所限定的范围。物面上各点成像光线的实际光路过于偏离理想路径，是理想成像所应有的物象之间的共轭关系遭到破坏，形成像差。因此，任何实用的光学系统，旨在校正其像差以达到良好的成像质量，都需要反复做大量的光路计算。

仍以双胶合望远镜的目镜为例，以单色光的轴上点球差为对象，用MATLAB计算并分析像差。当透镜孔径较大时，光轴上某一点发出的光束经透镜不再交于一点，这种现象称为球差。对单色光而言，轴上点成像的不完善仅由球差引起(见球差示意光路)。由于像方截距L'是U或h的函数，则球差也必然是U或h的函数。但是L'与U或h之间被一套包括系统结构参数在内的光路计算公式所联系，无法把球差用U或h显函数形式表达出来。不过，可算出少数几条实际光线后，用最小二乘法拟合出U或h多项式函数。由于光束对光轴的对称性质，δL'的多项式中只能包含U或h的偶次方项，并且，只要计算子午面内的子午光线。可按下列公式组计算。

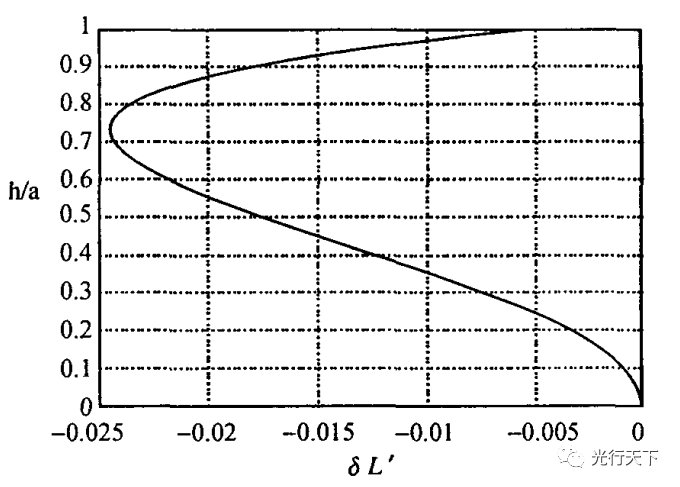
图3.球差一光线高度曲线图

4.结束语

借助脚LAB强大的矩阵计算功能，优秀的数值处理算法以及方便快捷的图形可视化特点，来解决几何光学中的理想光具组计算及像差分析，应该是一种有效的工具。

　　审核编辑：汤梓红