

怎样使用Python计算曲线的切点?
电子说
描述
曲线是数学中的一个基本概念,它可以定义为一种平滑的、连续的、无限延展的函数图像。在平面直角坐标系中,曲线通常由函数y=f(x)表示,其中x和y是变量,而f是函数关系。
切点是指曲线上的一个点,在该点处曲线的切线存在且垂直于该点处的切线。换句话说,切点是曲线在该点处的斜率等于该点处切线的斜率。
在数学中,通常使用导数来找到曲线在某一点的切线,它可以用于计算函数图像上某一点处的斜率。因此,为了找到曲线在某一点的切线,首先需要计算该点处的导数,然后找到与该导数相对应的x和y值。这些值就是切点。
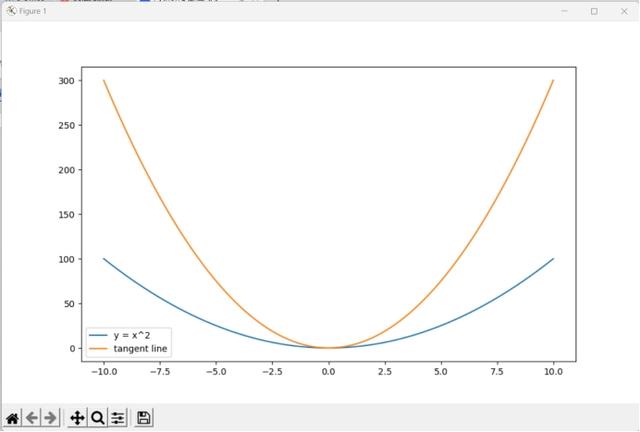
以下是一段使用Python的matplotlib库绘制曲线并计算切线的示例代码。这个例子会绘制一个简单的二次函数(比如y = x^2)的图像,然后在其上一点计算切线。
import numpy as np
import matplotlib.pyplot as plt
定义二次函数
def f(x):
return x**2
定义导函数
def df(x):
return 2*x
生成x的值
x = np.linspace(-10, 10, 400)
计算y的值
y = f(x)
计算切线的斜率
dx = 0.01 # 这是x的增量,可以根据需要进行调整
dy_dx = (f(x + dx) - f(x)) / dx # 根据定义,斜率等于函数值的增量除以x的增量
绘制原始函数图像
plt.figure(figsize=(10, 6))
plt.plot(x, y, label='y = x^2')
绘制切线
plt.plot(x, y + dy_dx*x, label='tangent line')
添加图例
plt.legend()
显示图像
plt.show()
这段代码首先定义了一个二次函数f(x) = x^2和它的导函数df(x) = 2*x。然后,使用numpy得linspace函数生成了一组从-10到10的等间隔的x值,并根据这些x值计算对应的y值。
然后,通过改变x的值(增量为dx)并计算函数值的增量,来计算切线的斜率。最后,使用matplotlib得plot函数来绘制原始的二次函数和切线,并通过show函数显示图像。
-
python怎么计算IV值2020-03-30 1545
-
Python遇上物联网又会碰撞出怎样的火花呢2021-08-27 2402
-
python nodemcu_python开发nodemcu的过程是怎样的?2022-02-15 1197
-
怎样使用计算法得到呼吸曲线PWM波和SPWM波呢2022-02-17 2044
-
缓和曲线计算软件工具2011-05-28 785
-
圆曲线坐标计算程序_软件工具2012-02-26 911
-
步进电机加速曲线计算器下载2018-02-05 1110
-
怎样使用PySerial接口Python和Arduino2019-11-04 4642
-
Python科学计算与数据分析2021-06-01 927
-
Python科学计算利器Anaconda2021-09-18 777
-
Python 梯度计算模块如何实现一个逻辑回归模型2023-10-21 1065
-
S曲线的基本变换计算2023-10-26 3420
-
python怎样运行代码2023-11-22 2845
-
不同壳温下SOA曲线的计算方法2023-12-04 1965
-
【smt工艺】无铅锡膏炉温曲线怎样设定?2024-03-20 3212
全部0条评论

快来发表一下你的评论吧 !

