通向大贝里曲率的新途径简析

包括小编在内的黎民百姓，崇尚眼见为实，在周围实空间中看到什么就描述什么。这是认识客观世界的基础，所以物理人注重描绘物体的大小、形状及其运动。后来，为了方便描述衍射物理，也基于对固体相互作用的深刻理解，物理人构建了实空间的倒易空间、动量空间或波矢 k 空间 (含时空间)。Whatever，将观测到的运动世界 map 到 k 空间中去，显示了颠倒世界的无尚风景。这种倒置的“对应”关系，构成了今天物理人、特别是凝聚态物理人的研究平台之一。看起来，物理人似乎形成了某种“条件反射”：实空间的世界里有什么，就要尝试在 k 空间中探索类似的效应。由此，k 空间中的“布里渊区”，亦成为波函数的三维坐标空间。这种倒置的三维空间，成为量子材料讨论问题的主体世界，反倒是实空间的物理显得有些 low 了。

当然，量子材料的主要任务，不是去关心材料实空间的显微结构和力学性能，不是去关心其加工成型和操控，而是更关注其中的量子载体──电子的集体运动行为，表现为 k 空间中波函数的形状、相互作用和运动好坏快慢等。

举个例子，对实空间一物体，为了某种目的，可以切割、剪裁物体的大小和特定形状，为我所用。也可利用简单力学原理做成角材、工字材，减轻物体重量而依然保持原来的性能品质。还可以利用对称性构建各种图案 (如蜂窝点阵、kagome 点阵、Penrose 拼盘等) 以显示美感和更多功能。更可以将其扭转、对接而制作成“莫比乌斯带”一般的拓扑非平庸几何结构。如此等等，形成了今天材料使用的各种行业，使得日常生活更方便、高效和舒适。这样简单的处理加工理念，物理人也希望运用到 k 空间的“物体”上，希望如此这般地实施后，也得到类似效果。当然，这里所谓的“物体”，就是能带。这里的所谓“效果”，就是量子材料能带的各种形态、尺度、相互关系及其对应于实空间的输运与转换性能，对吧？！小编外行，只是班门弄斧，从几个点上罗列编撰一些线条。

许多年来，物理人特别关注费米能级附近能带的方圆疏密、尖宽胖瘦，从而能对量子输运和光电转换等过程的快慢深浅、各向异性一览无余，如图 1(A) 所示。金属和半导体科技，从这一“方圆疏密、尖宽胖瘦”中获得了众多发现、革新和应用，不一而足；也促成能带理论成为凝聚态物理的核心。后来，固体物理引入自旋自由度，建立了金属磁性微观理论，勾画了上下自旋能带劈裂 shift 成铁磁金属，对能带理论亦有推动与发展。不过，即便到这一步，物理人还是很少对能带的整体或局部几何性质给出清晰认识、并加以操控。他们做得最多的，是将费米能级处的载流子迁移率和有效质量等物理量提取出来，并与能带色散、自旋磁矩等相联系，以改善材料性能。

对能带整体几何形貌和局部几何的特别关注，可能起始于非常规超导或电子关联物理。或者扯得更远一些，起始于费米能附近那些能标较小的物理效应 (例如拓扑、自旋相关激发、平带、自旋 - 轨道耦合 SOC 等)。图 1(B) 示意了其中一些简单情形，让读者感受到量子凝聚态的快速发展态势。到了今天，物理人已习惯于关注能带的整体几何性质，使之成为拓扑量子物理研究的核心。图 1(C) 所示的，即是能带整体几何性质的一种表现，也是本文即将触及的主题。

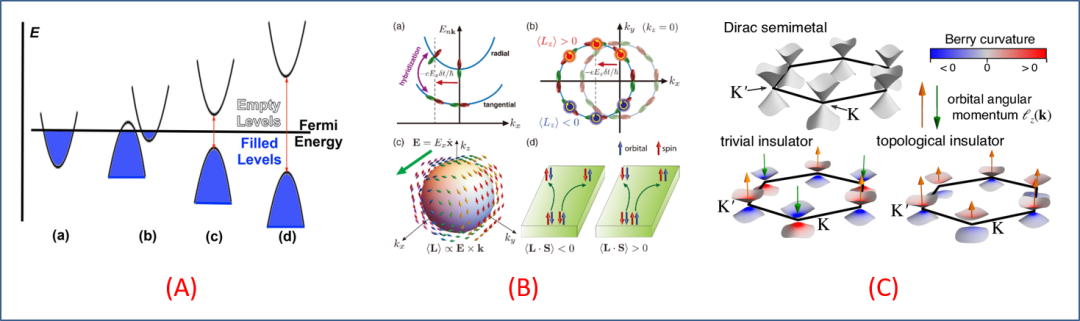
图 1. 物理人擅长描绘的 k 空间能带结构之几个例子。(A) 固体电子态最简单直观的表达，包括金属 (a)、半金属 (b)、半导体 (c) 和绝缘体 (d)。(B) 在 k 空间中，电子自旋和轨道自由度相关物理的一种展现，包括自旋 - 轨道耦合 SOC、轨道霍尔效应 OHE (orbital Hall effect) 等。(C) 在 k 空间中，狄拉克和拓扑量子体系的贝里曲率，其中狄拉克锥 (Dirac cone) 处贝里曲率用颜色表示、轨道角动量用箭头表示。

总之，物理人似乎养成了一种习惯或条件反射，不自觉将实空间和 k 空间对照一番、比划一下。不知道这是否正成为发现新物理、构建梳理新思路的一把密钥！当然，这种对照，也可能源于物理人进行的形象类比和通俗科普，以便更多人理解并给予支持，即便这样的类比有效或无效、严谨或粗糙。不过，相互颠倒的两重世界之间，如果存在某种对应或镜像，哪怕是类比，只要能更新或深化物理人对客观世界的理解，也未必不是好事。且看小编在囫囵吞枣之后，如何比划这种类比、对照。不妨选择实空间的电磁学及其 k 空间的类比，作为讨论的切入点。

选择电磁学作为议论对象，乃是因为电磁学可能是经典物理学表现最丰富和最亲切的分支学科。物理人任何时候去“一步三回顾”电磁学或电动力学，都可能有新收获：

(1) 电磁学主要讨论两个基本物理量，即实空间的电场 E 和磁场 B (磁感应强度)。前者是矢量、径向指向而一往直前，后者是赝矢量、轴向 (横向) 指向而环绕往复。前者对电荷的作用是电场力、点乘；后者对运动电荷的作用是洛伦兹力、叉乘。电场和磁场的这两类属性，驱动电子作纵向和横向运动。或者更一般地，它们一起驱动电磁场组合运动，构成电磁输运的基础。很显然，因为电场、磁场都能对运动电子施加作用，在固态量子体系的 k 空间中，它们也应该是主角。物理人希望由此在 k 空间中创造一个“电磁学”的世界，创造出类比电场或磁场的新物理量。当然，电场这一与时间无关的极矢量在 k 空间中依然可用，但 k 空间中类比于磁场的物理量之意义就不那么清晰。

(2) 凝聚态物理中，展示电磁场、特别是磁场主角形象的最佳场景，肯定是霍尔效应了。图 2(A) 所示为霍尔家族的主要成员。电场驱动载流子纵向运动，给了磁场驱动其横向霍尔漂移的机会，这是基本认知。接下来，如果存在一个等效磁场 (如铁磁材料的磁矩，就是等效磁场)，则反常霍尔效应就能登堂入室。一般情况下，反常霍尔会很显著，堪比强磁场下的正常霍尔。因此，反常霍尔是很强的物理，必定有更深刻的起源。这两大效应在物理人的研究中日久弥新，给凝聚态物理和量子材料以巨大影响。磁场或磁性，及至与磁性相关的自旋自由度和磁矩序参量，也早就成为凝聚态物理的重要内涵。

(3) 量子霍尔效应，超越正常和反常霍尔效应，早就粉墨登场了。以二维电子气中的霍尔效应为例：随磁场 B 变化，霍尔电阻呈现漂亮的霍尔平台。物理人对此的理解是，填充于费米面附近能级的电子，在磁场 B 作用下将回环运动。因为电子能级是离散化的，即所谓朗道能级，所以就有了霍尔台阶。此时，如果二维电子气是非磁性的，观测到的就是量子霍尔效应。如果体系是磁性的 (例如铁磁性)，则二维电子气可以呈现反常量子霍尔台阶，虽然这样的效应一直到 2010 年代才在磁性拓扑绝缘体中观测到。

(4) 无论是经典还是量子霍尔，外加磁场或等效磁场都是必要条件。对电磁学，磁场 B 的存在也是电子横向漂移运动的必要条件。如果再从微观机制层面看，由经典洛伦兹力到量子的朗道能级，磁场同样不可或缺。如果一定要较真这一说辞，不妨回顾一下电动力学中的 AB 效应 (Aharonov -Bohm 效应)。此时，物理人似乎初步“放弃”了直接讨论磁场 B，转而用经典电动力学中的磁矢势，再引入量子力学中几何相位概念，就可以理解 AB 效应了，如图 2(B) 所示。这里有两个层面的意涵。其一，AB 效应提升了磁矢势概念的重要性，它与磁场 B 至少存在数学上的联系 (磁场、磁通、磁矢势)，且磁矢势远比磁场的意义深刻。其二，虽然磁场 B 不在两束电子束运动路径上 (即电子束没有被施加洛伦兹力)，但改变 B 依然可以影响两束电子束的叠加干涉效果。干涉图样 shift 的方向，正是与电子束运动方向和磁场 B 方向正交的方向，这与霍尔效应的空间几何关系有类似之处。

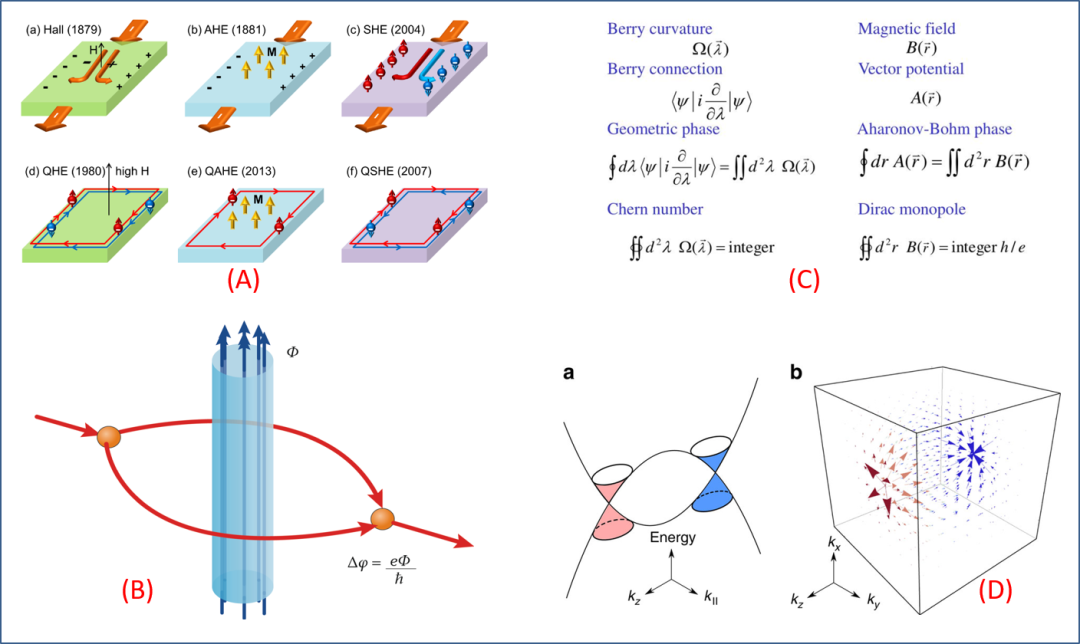
图 2. (A) 霍尔效应家族。(B) 在 k 空间中的贝里相位物理，与在实空间中的电磁学之间，存在某种对应关系。(C) 连接实空间电磁学和 k 空间量子力学之最简单图像：AB 效应。(D) 拓扑半金属的能带结构 (tilted Dirac cones) 和对应的贝里曲率分布。

如上 (1) ~ (4) 的逻辑梳理，让物理人感受到，对霍尔效应的认知，正逐渐从“磁场诱发的效应”过渡到“部分与磁场相关的效应”，最终到达“与磁场无关的效应”。正是如此，霍尔效应最终也成为展示量子凝聚态或量子材料效应的良好平台 (可能是最重要的平台)。最近受关注的“非线性霍尔效应”就是一个例子。它显性上与磁场 B 没有关系，表现为纵向电场驱动下的横向倍频电压信号。这些认知过渡的背后，是对量子力学中几何相位的深刻认识。所谓几何相位，也就是 k 空间中的贝里相位 (Berry phase)，如图 2(C) 所示。AB 效应中，两束同源而被分开的电子束在远处的干涉叠加，会对磁场变化产生响应，在实空间中是很匪夷所思的。但是，如果从磁场携带磁通引发磁矢势背后的贝里相位变化角度去理解，我们马上明白：正是因为贝里相位的变化，两束电子束在叠加时才会因为这一相位差而使干涉图样发生 shift。

行文至此，小编的感觉是：贝里相位与此处讨论的实空间物理之间，既并无明确的联系，亦有某种内在联系。毕竟，“霍尔效应源于磁场 B 的横向力作用”这一图像，在物理人脑海里太深刻了。因此，将 k 空间的贝里相位与实空间的霍尔效应进行类比，进而建立贝里相位与磁性之间的联系，就非常重要。这种联系的建立，产生的主要结果是：在 k 空间中，贝里相位就是 AB 效应中的磁通；而贝里相位连接 (Berryconnection) 即是磁矢势；归结到最后，贝里相位在 k 空间的变化剧烈程度 (实际上是贝里连接的 k 空间导数)，即是 (或比例于) 贝里曲率 (Berrycurvature)，也就是等效磁场 B。这样的类比，可以漂亮地描述 AB 效应，成为今天理解电磁效应的量子基础。注意到，贝里相位和贝里曲率，是在 k 空间中定义的，而波矢 k 含时间坐标。也就是说，对称性的类似性，让贝里曲率与磁性 (磁场) 依然是有联系的，并展现了超越简单类比的深刻物理。图 2(D) 所示，乃是 k 空间贝里曲率分布的一个实例。

现在，于 k 空间中，物理人也有了贝里曲率 (贝里相位、贝里连接) 这样与实空间的磁场 B (磁矢势、磁通量) 对应的物理量，只是这些物理与磁场 B (包括磁性、磁通、磁矢势) 之间已经没有显性的联系。“没有联系”就可以让物理人超越传统磁性的束缚，将贝里物理推广到所有可能达到之处，如非磁性、无特定对称性要求、无 SOC、无自旋 - 晶格耦合，等等 (只是经典物理意义上的扩展^_^)。姑且大胆幻想，在 k 空间中，物理人可以试图建立一套与经典磁性无关的“电磁学”，并发展相关的物理和应用。基于永不满足的性格，物理人马上就开始了 k 空间 (能带空间) 中诸多“电磁学”性质的探测。例如，贝里曲率对整个布里渊区的积分，就是二维拓扑绝缘体的拓扑陈数 (Chernnumber)。再例如，对金属磁性，贝里曲率对布里渊区所有填充态的积分，即为反常霍尔效应，或者干脆就是贝里相位。这些性质，与磁场 B 没有显性联系，虽然依然受到电场 E 的掣肘。

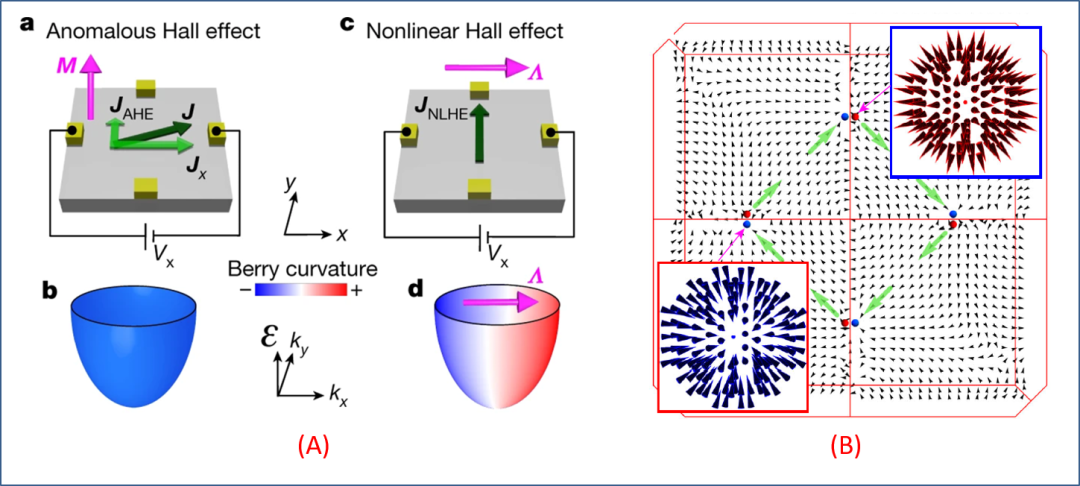
图 3. (A) 反常霍尔效应 (a) 对应于贝里曲率 (b)；非线性霍尔效应 (c)对应于贝里曲率一阶矩 (d) (颜色不同对应于贝里曲率的变化，形成 dipole 偶极矩 Λ)。(B) 在非磁性、中心反演对称破缺的化合物 TaAs 中，贝里曲率的分布和对应的磁单极子形态。

如果只是基于小编学过的若干三脚猫知识，是远不够去认识物理人如何探索 k 空间的“电磁学”的。小编只有一些碎片化的事实描述，姑且呈现如下，以滥竽充数：

(1) 测量贝里曲率的方法。很显然，能够有效测量贝里曲率，是讨论贝里相位物理的前提。实验上，要测量一个量子材料的能带几何形态，可以利用角分辨光电子能谱 APRES 和利用 STM 微分电导谱。它们都是成熟技术。但用它们去获取贝里相位和曲率，似乎并无特定优势。目前常用的方法，是测量平面霍尔电阻 (planar Halleffect, PHE)、量子振荡和非线性霍尔效应等。前两者依赖于外加磁场，不在此讨论。后者则对应于 k 空间贝里曲率的一阶偶极矩 (Berrycurvature dipole, first moment of Berry curvature)，如图 3(A) 所示。很显然，那些偶极矩很大的体系，也必定是贝里曲率很强的体系。

(2) 追求大贝里曲率的材料。即便是从贝里曲率和磁场 B 之间的简单类比，物理人也能明白，铁磁金属和半导体体系中一定有很多大贝里曲率的体系。事实也是如此，包括万贤纲一开始就预言的磁性外尔半金属。除此之外，中心反演对称破缺的非磁性体系也可有非零贝里曲率，著名的 TaAs 就是一个例子，如图 3(B) 所示。外尔半金属中的外尔点，其实就是贝里曲率奇异点。正因为贝里曲率类比于实空间磁场 B，物理人才将外尔半金属中一对一对的外尔点说成是 k 空间中的“磁单极”。当然，这里的“磁单极”，并非经典电磁学中的“磁单极”，或者说此“磁单极”非彼“磁单极”。推而广之，物理人还发现，在诸多 type - I 和 type - II 外尔半金属中，那些倾斜扭曲 (tilted) 的外尔锥处不但有很大的贝里曲率，且其一阶矩也可以很大，如图 2(D) 所示：它们都是大贝里曲率的材料。

(3) 在发现具体材料之外，物理人也关注有哪些典型晶体结构可以有很大的贝里曲率。例如，诸多二维结构的贝里曲率可以很大，特别是那些具有垂直镜面对称 (点群 Cs) 的结构。具有面外旋转对称轴的结构、面内六角或三角对称结构、魔角结构等二维结构，即便是完全没有 SOC 的体系，依然可以有很大的贝里曲率及一阶偶极矩。

寻找大的贝里曲率及其一阶矩的各种探索，在过去几年显得非常热火，也诞生了诸多成果，让物理人发展 k 空间高品质“电磁学”的努力受到很大鼓舞。不过，这样的探索，依然面临材料种类和物理约束过于严苛的局面，即便到今天，从更原理层面去寻求一些可能的新体系，依然充满挑战和诱惑。正因为如此，时常会有一些令人一时不解、但不久却会眼睛一亮的思路和尝试冒出来，让人回味而辗转。

果不其然，来自意大利萨莱诺大学物理系 (Dipartimento di Fisica, Universita diSalerno) 的量子凝聚态理论学者 Carmine Ortix 教授 (他最近几年十分活跃和高产)，带领他的团队，与瑞士 University of Geneva 的量子材料知名学者 Andrea D. Caviglia 合作，近些年一直致力于拓扑量子材料的探索。最近，他们于前人工作基础上提出，在非磁性、非中心对称的晶体结构中，即便没有空穴激发 (hole excitations)，依然可以由晶体场诱发出一些贝里曲率高度浓缩集中的区域，给 k 空间“电磁学”带来实空间电磁学所没有的别样风景。

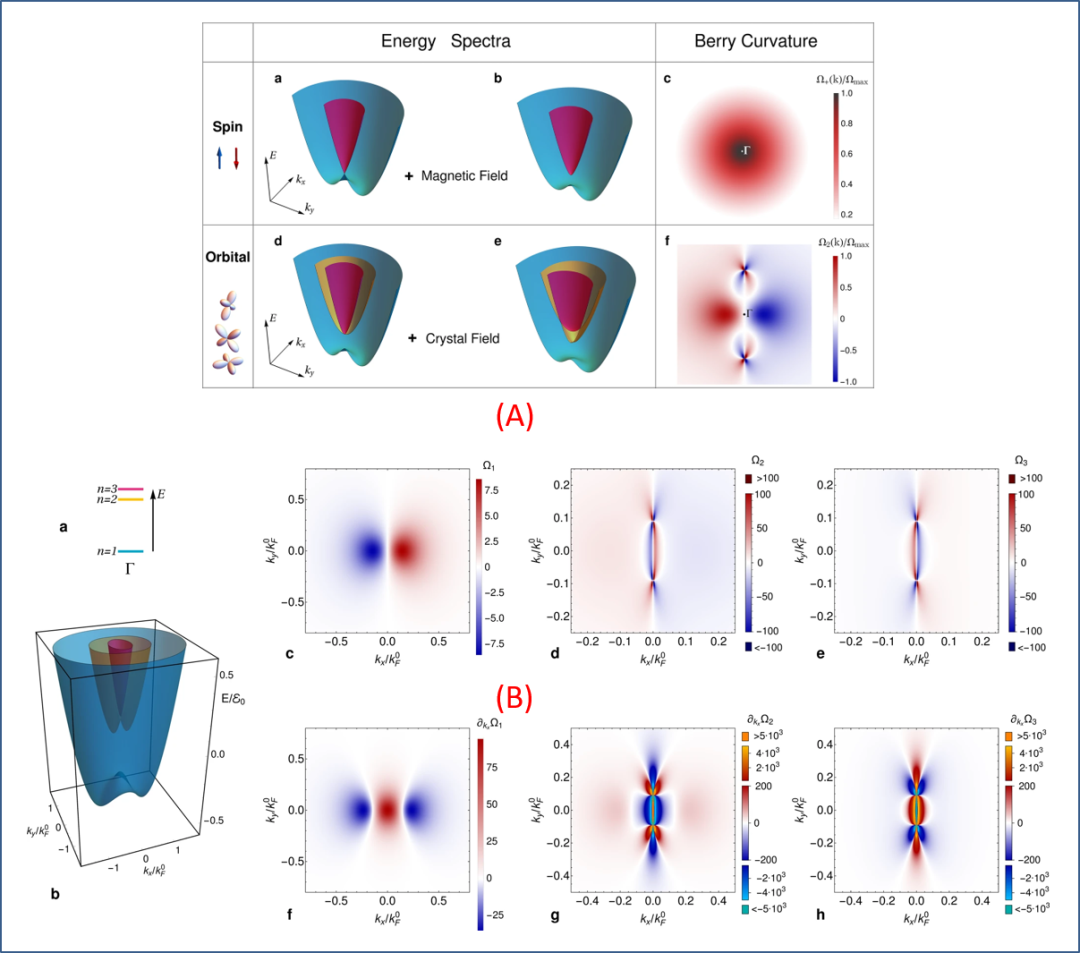
图 4. 由晶体场诱导的轨道角动量可以调控贝里曲率：(A) Spin and orbital mechanisms of Berry curvature。(B) Orbital design of Berrycurvature hot-spots and pinch points。

Ortix 他们的这一工作，侧重于理论构建和推演，对小编阅读理解构成巨大势垒。小编且先将部分结果集成于图 4 中，再写几段囫囵吞枣式的读书笔记：

(1) 在非磁性及 SOC 很弱的体系中，贝里曲率很强的结构应该不多。毕竟没有等效磁场对能带劈裂的加持效果，形成大贝里曲率并不容易。

(2) 那些中心反演对称破缺之拓扑半金属体系，如 TaAs 等，当然可以有很大的贝里曲率及一阶矩 (dipole,first moment)。不过，这样的体系，加上外尔半金属的特征，需要外尔点处电子和空穴共同激发、叠加，才能实现大的贝里曲率效应。这一要求有些严苛，满足要求的体系可能不那么多。另外，贝里曲率大的区域，主要围绕在外尔点附近。而空间反演对称破缺诱发的外尔半金属，其布里渊区内形成的外尔点密度并不高，故而 k 空间整体贝里曲率就不大可能很大。

(3) Ortix 他们通过深入理论分析，似乎找到了一类具有特定轨道自由度 (轨道角动量) 的电子结构，即便不存在费米面处的空穴激发，即便没有磁性、没有自旋 - 轨道耦合 SOC，只要其晶格对称性足够低 (例如点群 C3v 和 Cs 等对称性)，就可以通过晶体场分裂能带，形成若干所谓的贝里曲率会聚区 (Berrycurvature hot - spots) 和奇异夹点 (Berry curvature singular pinchpoint)，从而实现贝尔曲率及一阶偶极矩显著增强。当然，轨道自由度对拓扑能带的影响，前人已经有相关研究，并非 Ortix 他们的原创。

(4) 基于以上分析，Ortix 他们还给出了具体的候选材料，并建议后来者去实验验证。他们指出，具有较强晶体场和晶格畸变、数目众多的钙钛矿 ABO3 过渡金属氧化物家族中，就存在很多这样的体系，包括由 SrTiO3、KTaO3 和 SrVO3 等组成依 (111) 面构成的异质结体系，可能实现大贝里曲率效应。那些 (111) 面取向的低维晶体，也可能具有很大的贝里曲率。

应该说，Carmine Ortix 他们的这一工作，提出了一类基于晶体场和轨道自由度 (轨道角动量) 操控 k 空间贝里曲率的理论方案，并预言几类非磁性、无 SOC 的过渡金属氧化物低维结构可以实现大的贝里曲率和大的非线性霍尔效应，给了 Ising 胡诌的“k 空间电磁学”以正面素材。随后，Ortix 他们也宣示这一理论对所谓的“轨道电子学”做出了创新性贡献，并展望了这一理论框架在未来的狄拉克准粒子物理、电声相互作用物理中所起的作用。从这一角度看，轨道自由度诱导的大贝里曲率效应，是有意义的、值得后来者跟随和进一步探索的新物理。需要特别指出，基于轨道自由度的霍尔效应 (如 OHE)，已经见诸报道，但借助晶体场实现大的贝里曲率这一思路和尝试，却是他们新的、有意义的贡献。

审核编辑：刘清