

次谐波震荡引起的开关电源不稳定
电源/新能源
描述
相信各位都会遇到DCDC不稳定的现象,例如补偿参数不合适,或是Layout不足所导致。
那么,大家对于次谐波震荡引起的开关电源不稳定,又还留有多少记忆呢?
今天,小编要带大家回顾下次谐波震荡,这个熟悉而又陌生的概念。
接下来,将以峰值电流控制的Buck电路为例,分别从时域和频域的角度出发,来为大家介绍下次谐波震荡。
0****1
认识次谐波震荡
时域角度
如图1所示,从Buck峰值控制方框图可见,参考电压Vref与输出电压Vout相减所得到的误差信号VC与电感电流信号IL进行比较,从而给出控制信号来驱动上管和下管。
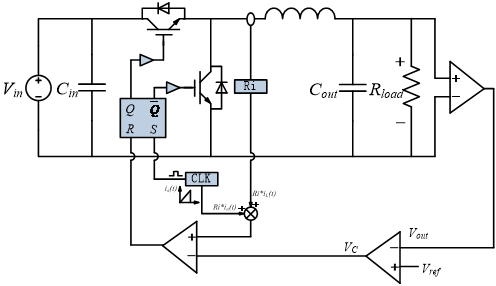
图 1:Buck 峰值电流控制方框图
如图2所示,可以更直观的看到VC和IL的“相遇”过程,其中,蓝色的线条表示稳定工况下的IL信号和开关波形SW,粉色的线条表示发生扰动后的IL和SW,定义∆I0和∆ton 为误差量。显然,从(a)和(b)图中可见,占空比Duty=30%,扰动量逐渐减小,系统趋于稳定,然而,Duty=70%,扰动量逐渐增大,导致系统不稳定。

(a):Duty=30%, I~L ~趋于稳定

(b):Duty=70%, I~L ~趋于不稳定
图 2:Buck 峰值电流控制原理
从上述几何的角度,大致可以推断出50%是扰动收敛与扰动发散的分界点,那么,严谨的攻城狮们当然也可通过公式的推导来得到这个结论,可先定义变量如下图3所示,D表示占空比;m1,m2表示电感电流的上升,下降斜率;ic1,ic2表示电感电流顶到VC时刻的值;iL (0),iLT(s)表示电感电流周期始末值;∆iL (0),∆iLT(s)表示扰动量周期始末值。

图 3:Buck 峰值电流控制原理(电感电流扰动波形)
有了上述变量,我们便可推导出如下公式:

可见,当D < 1/2,即Duty < 50%,在第n个周期,∆iLT(ns)会逐渐收敛为零,反之,若D > 1/2,∆iLT(ns)会呈发散状态。此外,可发现扰动量是正还是负,与n有关,变化率正好是开关频率的一半,故得名为次谐波震荡。
频域角度
以上,是时域角度对次谐波震荡的介绍,但大家是否曾从频域的角度来认识下次谐波震荡呢?我们根据图1,可得出图4中的系统结构图,从而推导出系统控制到输出的开环传递函数。

图 4:Buck 峰值电流控制系统结构图.
有了控制到输出的开环传递函数后,我们定义输入电压Vin=12V,开关频率Fs=400kHz的条件下,通过改变Duty,来观察其Bode图的情况。如图5所示,当Duty等于50%和67%时,在1/2的开关频率处,增益曲线会出现谐振峰,并且相位曲线快速翻转,这便是发生了次谐波震荡,严重影响了系统稳定性,然而,当Duty等于28%时,增益曲线和相位曲线均未发生异常。

图 5:G i-v (s) 函数 Bode 图.
02
消除次谐波震荡
针对上述次谐波震荡问题,锯齿波电流补偿技术可以解决这个问题,其原理就是在电感电流信号上叠加一个锯齿波补偿信号(如图6所示),从而使VC信号其从恒定值变为了一个脉动的斜坡信号,通常称之为斜坡补偿技术,其抑制效果可以参考图7。
当然,上述斜坡补偿的技术同样可以从数学推导和频域角度去分析,详细内容欢迎大家从小视频中寻找答案。

图 6:加入锯齿波补偿的 Buck 峰值电流控制方框图.

图 7:加入锯齿波补偿的 Buck 峰值电流控制方框图.
03
斜坡补偿的负面效应
斜坡补偿虽然可以抑制次谐波震荡,但在电源设计的过程中,我们需要考虑斜坡补偿所带来的负面效应。主要可概括出两点:1. 因斜坡补偿的加入,芯片的限流点会随着duty的增大而逐渐减小;2. 过大的斜坡补偿会影响到系统的动态性能。
从图8中可见,以MPQ4420A为例,Duty越大,限流点逐渐减小。

图 8:MPQ4420A 限流点与占空比关系曲线.
从图9中可见,Mc是斜坡补偿系数,补偿系数越大,系统带宽越小,从而系统的动态响应也会越慢。

图 9:加入斜坡补偿后的 G i-v (s) 函数 Bode 图.
-
开关电源如果调整才能保障稳定性2017-11-02 6993
-
开关电源中的不稳定的解决方案解析2021-03-16 19550
-
负压的输出不稳定是为什么2021-12-28 1417
-
电力系统谐波不稳定_赵贺2017-01-08 819
-
电荷泵式开关电源的基本电路 图片内容来自《开关电源设计入门》有资料介绍负压的输出不稳定,必要时需要增加稳压控制电路2022-01-05 739
-
机械不稳定与共振2022-07-08 1993
-
诊断和稳定不稳定开关电源的快速提示2022-08-05 4087
-
识别并消除次谐波振荡2023-08-02 1933
-
开关电源谐波如何解决2023-08-18 8616
-
伺服电机转速不稳定的因素2024-06-19 3578
-
运放输出不稳定是什么原因2024-07-13 5184
-
开关电源空载电压不稳定是什么原因2024-08-08 6415
-
反激式开关电源输出电压不稳定的原因2024-08-20 5281
-
稳压电源电压不稳定的原因2024-08-29 3379
-
JGN8-M18-OP接近开关信号不稳定怎么办2025-07-10 763
全部0条评论

快来发表一下你的评论吧 !

