

离散傅里叶变换及其应用简析
电子说
描述
傅里叶变换(Fourier Transform)是一种数学工具,用于将一个函数(通常是时间域函数)转换成另一个函数(通常是频域函数),以分析该函数的频率特性。傅里叶变换是工程、物理学、计算机科学、图像处理、音频信号处理以及量子物理等多个领域中常用的一种数学方法。
时间域和频域是信号或函数的两种不同表示方式,它们包含的是同样的信息,只是从不同的角度进行展示。傅里叶变换(Fourier Transform)和其逆变换(Inverse Fourier Transform)是从时间域到频域、以及从频域到时间域进行转换的数学工具。
通过傅里叶分析,你可以将一个时间域函数转换到频域来分析它,或者将一个频域函数转回时间域以重构它。这两种表示方式各有其优点和应用场景。例如,在信号处理、通信、图像处理等多个领域,频域分析提供了很多方便和高效的方法。
时间域函数
在时间域 (Time Domain) 中,信号或函数是按照时间变量 (通常表示为 t ) 来描述的。在这个表示中,你可以看到信号是如何随着时间变化的。时间域表示是直观的,因为它正是我们在现实世界中观察信号的方式。例如,声音波、电信号等都可以在时间域中表示。举个简单的例子,正弦波 Asin(2πωt+ϕ) 是一个时间域函数,其中 A 是振幅, ω 是频率, ϕ 是相位角, t 是时间。
频域函数
频域(Frequency Domain)表示则是关注信号各个不同频率成分的强度或相位。在频域表示中,信号被表达为一系列正弦和余弦波的组合,这些正弦和余弦波有不同的频率和振幅。这样的表示使得我们能更容易地分析和理解信号的频率特性。例如,傅里叶变换是一种常用的从时间域到频域的转换方法。在该变换后,将得到一个频域函数,通常表示为 F(f) 或 F(ω) ,其中 f 或 ω 是频率或角频率。
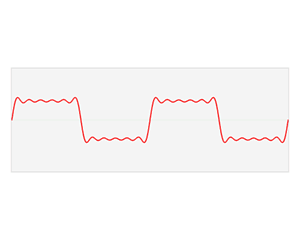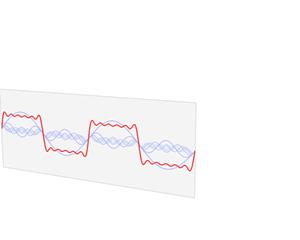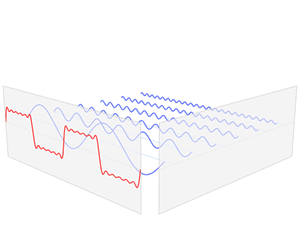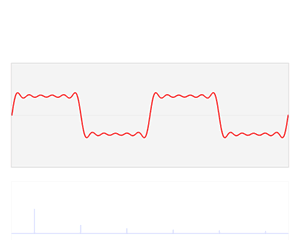
我们知道,任何周期函数在满足狄利克雷条件下 (连续或只有有限个间断点,且都是第一类间断点;只有有限个极值点),都可以展开成一组正交函数的无穷级数之和。使用三角函数集的周期函数展开就是傅里叶级数。对于周期为 T 的信号 f(t) ,可以用三角函数集的线性组合来表示,即
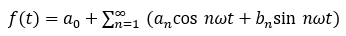
式中 ω=2π/T 是周期信号的角频率,也成基波频率, nω 称为 n 次谐波频率; 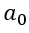 为信号的直流分量,
为信号的直流分量,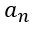 和
和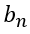 分别是余弦分量和正弦分量幅度。根据级数理论,傅里叶系数
分别是余弦分量和正弦分量幅度。根据级数理论,傅里叶系数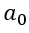 、
、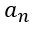 、
、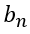 的计算公式为:
的计算公式为:
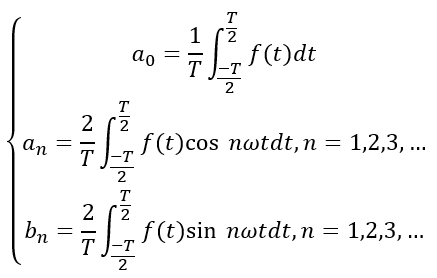
若将式子中同频率的正弦项和余弦项合并,得到另一种形式的周期信号的傅里叶级数,即
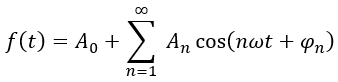
其中,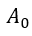 为信号的直流分量;
为信号的直流分量;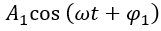 为信号的基频分量,简称基波;
为信号的基频分量,简称基波;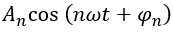 为信号的 n 次谐波, n 比较大的谐波,称为高次谐波。上式说明任何周 期信号只要满足狄利克雷条件,都可以分解成直流分量和一系列谐波分量之和,这些谐波分量的频率是周期信号基频的整数倍。比较两种三角函数形式的傅里叶级数,可以看出它们的系数有如下关系:
为信号的 n 次谐波, n 比较大的谐波,称为高次谐波。上式说明任何周 期信号只要满足狄利克雷条件,都可以分解成直流分量和一系列谐波分量之和,这些谐波分量的频率是周期信号基频的整数倍。比较两种三角函数形式的傅里叶级数,可以看出它们的系数有如下关系:
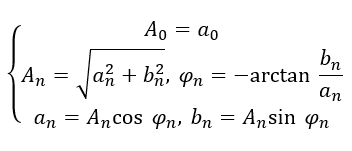
傅里叶变换适用于非周期性函数,将一个时间域函数转换为其对应的频域函数。可以将傅里叶级数看作是傅里叶变换的一个特殊情况。考虑一个周期为 T 的函数。如果 T 趋于无穷,这意味着函数是非周期性的,此时傅里叶级数会趋向于傅里叶变换。
连续傅里叶变换
对于连续函数 f(t) ,其连续傅里叶变换定义为:
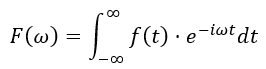
逆变换是:

离散傅里叶变换
对于离散信号,有离散傅里叶变换 (DFT) :
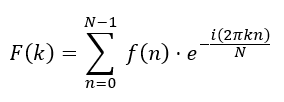
其逆变换是:
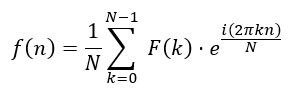
离散傅里叶变换在多项式乘法中的应用
对于n-1阶多项式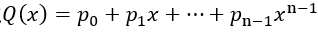 可以用n个点唯一表示(复数的点也是可以的)。令
可以用n个点唯一表示(复数的点也是可以的)。令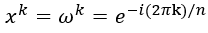 ,
,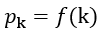 ,k=1,…,n-1
,k=1,…,n-1

只要我们可以求出矩阵的逆,就能反推出这个 Q 的系数。这个矩阵的逆的形式:
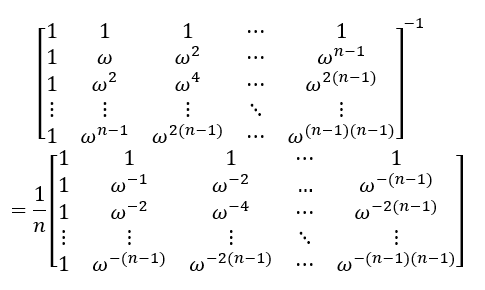
快速傅里叶变换(Fast Fourier Transform,简称FFT)是离散傅里叶变换(Discrete Fourier Transform,简称DFT)的一种高效算法。FFT能在 O(NlogN) 的时间复杂度内完成这一变换,而直接计算 DFT需要 O(N^2^) 的时间复杂度。
FFT基于一种名为“分治法”的递归策略,它将一个大问题分解为几个更小的子问题来解决。对于一个 N 点的DFT,FFT会把它分成两个 N/2 点的DFT,并递归地进行这个过程。
具体来说,FFT算法采用以下步骤:
- 分解阶段:原始 N 点DFT分解为两个 N/2 点的子序列,一个包含所有的偶数索引,另一个包含所有的奇数索引。
- 递归阶段: 对这两个 N/2 点子序列递归地应用FFT。
- 组合阶段:使用递归解的结果,通过一系列的复数乘法和加法,组合得到原始N点DFT的结果。
原始的DFT定义为:
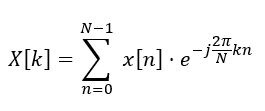
在FFT中,这个和会被分成两部分:一部分是偶数索引,另一部分是奇数索引:
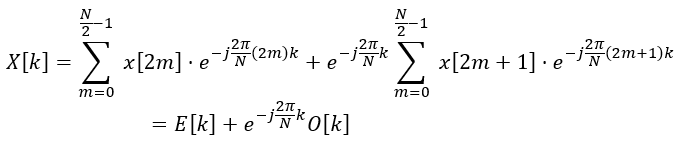
其中 E[k] 和 O[k] 是偶数和奇数序列的DFT。
具体例子
假设我们有一个 4 点的序列 x=[0,1,2,3] 。
- 分解
偶数序列 e=[0,2]
奇数序列 o=[1,3]
- 递归求解
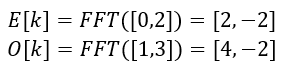
- 合并
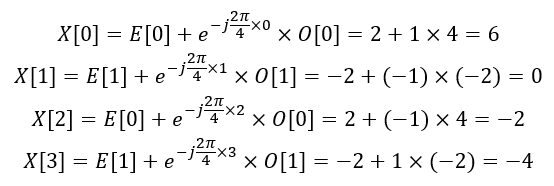
所以 X=[6,0,-2,-4] ,这就是序列 x 的DFT。这个过程大大减少了计算量,当 N 是2 的幂时,效率最高。
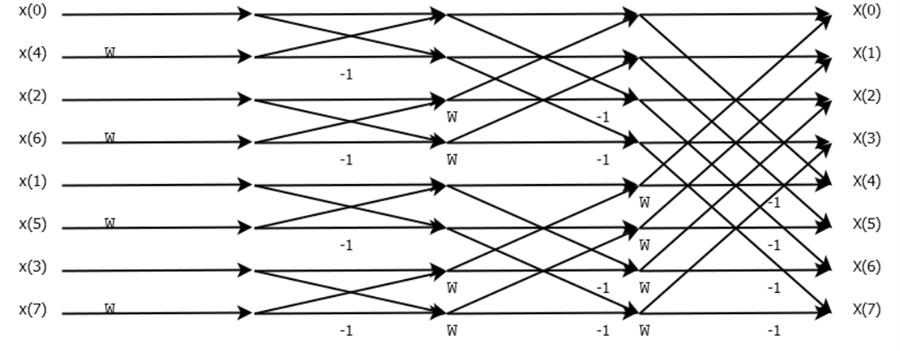
我们总结一下该过程的时间复杂度如下:
- DFT阶段: 将两个 n 度的多项式 A(x) 和 B(x) 使用FFT转换到点值表示,分别得到 A(k) 和 B(k) 。时间复杂度为 2×O(nlogn)=O(nlogn) 。
- 乘法阶段:在点值表示下,将 A(k) 和 B(k) 对应点值相乘得到 C(k) 。这是个 O(n) 时间复杂度的操作。
- IDFT阶段:再次使用FFT (实际上是其逆变换IDFT)将 C(k) 转换回系数表示得到 C(x) , 即 A(x)×B(x) 。时间复杂度是 O(nlogn) 。综合这三个阶段,总时间复杂度为 O(nlogn)+O(n)+O(nlogn)=O(nlogn) 。
数论变换(NTT)是有限域上离散傅里叶变化的一个变体。由于离散傅里叶变换是基于复数域上的变换,大多是浮点运算,故存在着一定的精度和效率问题。在许多应用中,需要对整数商环上的多项式进行变换,在这种情况下离散傅里叶变换的性能无法满足要求。而NTT直接对整数进行处理而无需考虑浮点数中的存储问题和精度问题,避免了浮点计算,大大提高了运算效率,非常适合基于LWE或RLWE难题的密码系统。
数论变换(NTT)是整数环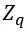 上定义的线性正交变换。设x(i),X(k)∈
上定义的线性正交变换。设x(i),X(k)∈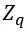 ,i=0,1,2…,n-1,k=0,1,2,…,n-1,有如下公式:
,i=0,1,2…,n-1,k=0,1,2,…,n-1,有如下公式:
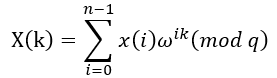
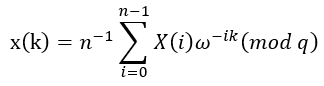
公式中ω为模q的n次单位原根,满足
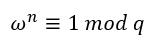
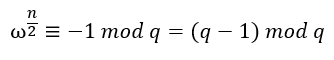
n为整数并且存在n^-1^满足
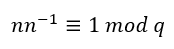
-
如何实现离散傅里叶变换2024-11-14 2301
-
傅里叶变换的定义 傅里叶变换的意义2023-11-30 3929
-
傅里叶变换的实现方法2023-09-07 2300
-
离散傅里叶变换(DFT)及其快速算法(FFT)2016-12-28 1072
-
离散傅里叶变换2016-06-06 604
-
如何用LABVIEW做一个关于离散傅里叶变换2012-04-08 7251
-
有限长离散变换-离散傅里叶变换2011-02-23 1232
-
离散傅里叶变换及其快速算法2008-10-30 967
全部0条评论

快来发表一下你的评论吧 !

