

Moog滤波器的小信号开环传递函数实现
电子说
描述
压控滤波器(VCF)是模拟合成器的支柱。但是有一个过滤器高于其他过滤器,因为它具有创造性、有效性,并且可听见地“出色”:moog阶梯滤波器。在本系列中,我们将分析moog阶梯滤波器的行为,从小信号开环分析开始。在上一篇文章中,我们讨论了过滤器的主要元素并分析了驱动程序部分。现在,我们将分析拓扑的核心(滤波器部分)并表示整个滤波器的小信号开环传递函数。在第1部分中,我们看到了moog阶梯滤波器的完整原理图,并将其缩小为图1所示的形式。
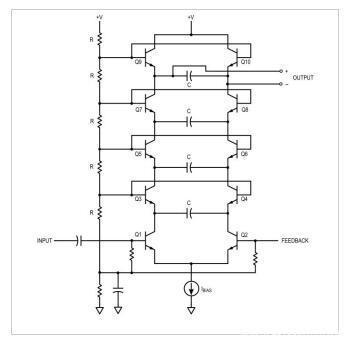
图1.moog过滤器
将拓扑分为三个元素:一个驱动阶段;中间过滤阶段;输出滤波器级。 这三个阶段如图2所示。
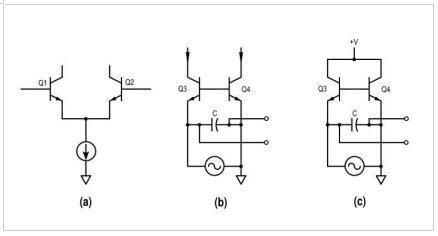
图2.梯形滤波器拓扑的三个元素(a)驱动差分对(b)中间阶梯低通滤波器部分(c)最顶部的输出滤波器部分。
同样在第1部分中,我们推导出驱动级中的电压和电流之间的关系,如图2(a)所示。现在将分析图2(b)和2(c)所示的滤波器级。
Moog滤波器的各个滤波器
过滤器部分彼此相似,只是一个在梯子中驱动另一个阶段,而另一个阶段与供应相连。同样的机制在两者中都起作用,因此我们只分析图3中所示的机制。
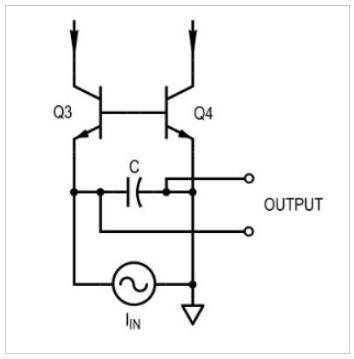
图3.moog滤波器中的一个滤波器部分,具有差分驱动电流。
对于小信号分析,可以进行以下简化,如图4、5、6和7所示。
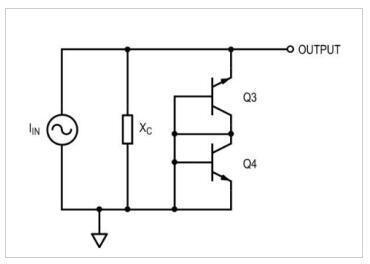
图4.使用基极保持恒定电位并将电容器作为电抗的事实。
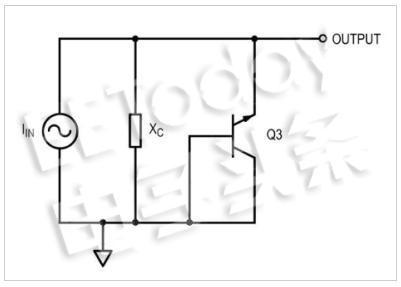
图5.移除短路晶体管。
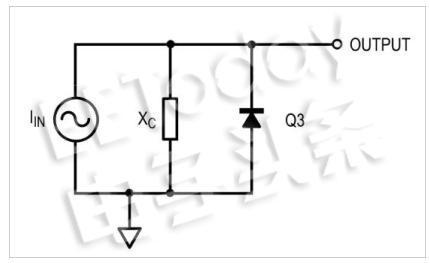
图6.晶体管Q3以二极管配置连接,因此可以用二极管示意性地替换它。
乍一看,图7中的电路可能看起来不像滤波器。
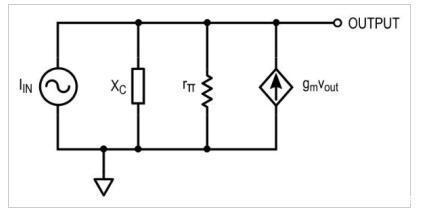
图7.最后将二极管/晶体管替换为混合PI模型。
这是公平的,看到这样的电流驱动RC电路并不常见。但是,注意到这两个并联元件起到了分流器的作用,而不是分压器的作用,它开始有意义了。随着电容电抗X c减小(随着频率增加),电容器两端的电压降低。该电路的输出电压是电容两端的电压,并将传递函数描述为跨阻抗rtr,发现:

对于晶体管偏置(驱动)电流IC,我们假设高β。对于中间滤波器级,输出电流gmvout输入到下一部分的输入电流。这个电流是:
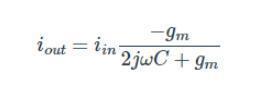
这是我们计算开环增益所需的唯一结果。总结一下这个滤波器部分:我们已经证明输入电流会在电容上产生电压降,这与电容电抗成正比。随着频率的增加,电压降低,这给了我们低通的作用。它就像电容器和晶体管等效基极阻抗(跨导)之间的电流驱动RC滤波器。对于中间级,晶体管电流用作下一部分的输入电流,而电容器电压本身则作为最顶级的输出。
综合起来计算开环增益
我们已经描述了驱动程序和滤波器部分的传递函数。现在我们准备计算开环增益。对于n个滤波器级,我们可以结合之前的结果(驱动器、n-1个中间阶梯滤波器部分和一个输出滤波器部分),并找到输出电容的左侧为正:
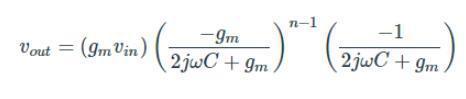
这简化为:
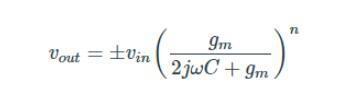
其中vout为n偶数的正数,n奇数的负数。开环电压增益为:
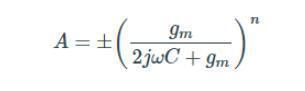
利用gm近似等于1/re′的事实,我们可以重写这是一个更熟悉的形式,
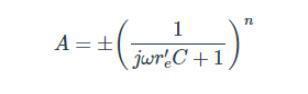
你可能会注意到,它非常类似于RC低通滤波器的传递函数,
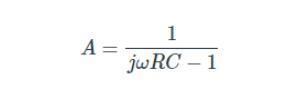
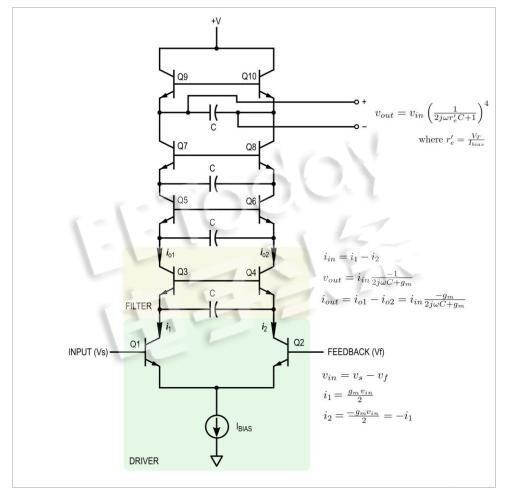
图8.moog梯形滤波器特性总结。
总结穆格滤波器的行为如下(见图8):偏置电流设置晶体管的静态点,该电流在阶梯的两侧共享。忽略反馈,左侧的输入电压驱动通过分支的小信号电流。分支之间的差分信号在电容器之间产生电位差,允许滤波发生。一种方法是晶体管的跨阻抗产生带有电容器的RC滤波器。
作为最顶层电容器的电位的输出取决于流过该电容器的小信号电流。到目前为止,假设了一些重要的事情:所有晶体管共享相同的β(即它们都匹配);通过每个晶体管的基极的电流可以忽略不计;晶体管充当理想的相关电流源(无厄利效应);所有晶体管都偏置在有源区中;驱动级共模电压可以忽略不计;偏置电流源是理想的。
即使有这些理想化,电路也会受到温度依赖性的影响(隐藏在gm术语和晶体管β中)。但是,该电路曾用于模拟合成器,这些缺陷被认为是过滤器的特性。
总结
在第二部分的分析中,研究了著名的moog阶梯滤波器的小信号行为。做了一些重要的假设和理想化来简化分析,并得出了n级滤波器的通用传递函数。未来将通过考虑反馈来扩展分析,并更详细地分析滤波器部分以理解滤波器参数。moog阶梯滤波器也激发了一些模仿猫的设计,我们也将对它们进行研究。
-
Sallen-KEY滤波器传递函数问题2025-09-24 4535
-
低通滤波器传递函数 低通滤波器原理2024-01-30 6309
-
低通滤波器电路特点 低通滤波器传递函数怎么算2024-01-24 3740
-
带通滤波器的传递函数怎么获取?2023-11-16 923
-
一阶高通滤波器传递函数如何导致高通量和相位响应呢?2023-09-19 6180
-
开环传递函数是怎样影响系统的?2023-07-11 5723
-
有源滤波器中的低通和高通响应2023-02-01 6805
-
传递函数极点和零点的影响是什么2021-06-12 11278
-
低通滤波器的传递函数简介2017-11-29 161059
-
我想自己设计滤波器的传递函数,怎么在Labview中实现?2014-05-08 4582
-
请问模拟滤波器 传递函数有什么特点?2011-09-29 5076
-
传递函数中零点的解决方案2010-12-24 5094
-
二阶RC滤波器的传递函数表2009-05-08 13446
全部0条评论

快来发表一下你的评论吧 !

