一阶高通滤波器传递函数如何导致高通量和相位响应呢？

简要回顾一下：通过对S域电路的分析，可以得到低通滤波器的输入输出特性表达式；电路的VOUT/VIN表达式是滤波器的传递函数，如果将该表达式与标准化形式进行比较，可以快速确定两个关键参数，即截止频率和最大增益；传递函数可以写成分子多项式除以分母多项式，分子多项式的根是传递函数的零，分母多项式的根是传递函数的极点。另一种说法是传递函数零导致T（s）= 0并且传递函数极点导致T（s）→∞；轮询调查导致系统波特图幅度响应的斜率下降20dB/decade；零点导致斜率增加20dB/decade；轮询贡献-90°的相移，零点贡献+ 90的相移。

高通传递函数

一阶RC高通电路实现如下：

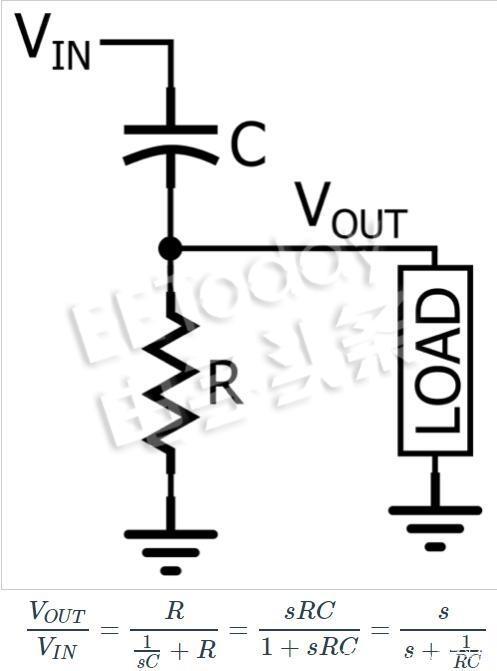
一阶高通滤波器的输入到输出行为可以通过以下标准化传递函数来描述：

将它与相应的低通表达式进行比较：

如你所见，分母是相同的。在这两种情况下都具有在s =-ωo处的极点，这意味着这两个低通滤波器和所述高通滤波器将具有以下特征：在ωo幅度响应将低于最大量值响应3分贝；使用无源滤波器最大幅度响应是统一，在这种情况下，在ωo的值为-3dB；在ωo电路的相移绝对值为45°。

因此，这两个电路中ωo处的响应非常相似。然而，ωo上下频率的响应受t（s）分子的影响T（S）分子的影响，这两个分子之间的差异使低通滤波器与高通滤波器有很大的不同。

分子作用

T（s）HP的分子告诉我们两件事：幅度响应的初始斜率为+ 20 dB / decade，最大幅度为1。让我们仔细看看这两个特征。

初始斜率

**由于在分子中有变量s，因此无论s的值是什么，我们都会有一个传递函数为零，导致分子等于零。在一阶高通滤波器的情况下，整个分子乘以s，因此零在s=0。s=0时的零点如何影响实际电路的振幅和相位响应？首先考虑一下它的大小。我们知道零点将导致波特曲线的斜率增加20dB/decade。然而，这种增加发生在ω=0rad/s（或=0Hz），这里是捕捉点：波特图的水平轴永远不会达到0Hz。它是一个对数轴，这意味着频率从10Hz降至1Hz，降至0.1Hz，降至0.01Hz，依此类推。它永远不会达到0Hz。因此，我们从未在ω=0rad/s处看到零点的角频率。**

相反，幅度曲线仅以+ 20dB/decade的斜率开始。幅度继续增加到极点频率；极点使斜率降低20dB/十倍，导致响应变得平坦（即斜率=0dB/十进制）并且随着ω向无穷大增加而保持平坦。

最大增益

我们所需要的是一些数学操作，以确定高通滤波器的最大增益将等于a1。从高通滤波器幅度响应的一般形状，我们知道增益不会随着ω向无穷大增加而减小。因此，我们可以通过评估s→∞的T（s）来找到最大增益。在分母中，我们有S +ω 。加在无穷大上的东西是无穷大，所以在这种情况下，我们可以将T（s）简化为：

分子中的s和分母中的s抵消了，所以

高通滤波器相位响应

如上所述，零点对系统的相位响应贡献了+ 90°的相移，在零频率处有+ 45°的相移。相移在零频率以上十倍的频率达到+ 90°，但高通滤波器在ω= 0 rad / s时为零，并且无法指定高于0的十倍频率rad / s。我们在这里处理对数标度，这意味着水平轴永远不会达到0 rad / s，也不会达到高于0 rad / s的十倍频率（这样的频率）并不存在：0 rad / s×10 = 0 rad / s）。所有这些的结果是高通滤波器相位响应具有+ 90°的初始值。换句话说，所有低频输入信号将移位+ 90°，然后随着输入频率接近极点频率，相移将开始减小：

总结

我们已经研究了一阶高通滤波器的标准传递函数，我们已经看到了这种传递函数如何导致高通量和相位响应的特性。