DDFM：首个使用扩散模型进行多模态图像融合的方法

本文是西安交通大学&苏黎世联邦理工学院的赵子祥博士 在ICCV2023上关于多模态图像融合的最新工作，题目为：DDFM: Denoising Diffusion Model for Multi-Modality Image Fusion。本文首次在多模态图像融合领域采用了扩散模型，很精彩的一篇工作，就是数学推导难住了我这个工科生。本文提出的模型DDFM的完整流程是通过图1的c来实现，而具体到每一步从 fT 到 fT−1 的过程是通过图3的流程实现，也就是本文的核心之一：传统vanilla DDPM模型中有 ft → f~0|t → ft−1 的过程，而本文会在 f~0|t 到 ft−1 之间通过EM算法增加一个中间量 f^0|t 来解决最大化似然问题（即解决下文中公式13），整个过程变为 ft → f~0|t → f^0|t → ft−1。而这个过程是为了解决本文另一个核心，即条件生成问题。具体则是将图像融合损失函数优化问题转化为最大似然问题。综上所述，可以这样理解本文DDFM的融合思想：首先通过自然图像预训练的DDPM模型进行无条件生成，得到初步结果（目的使融合结果符合自然图像的生成先验）。随后对初步生成结果进行条件生成（似然修正）。通过将融合问题转化为一个含隐变量的极大似然估计问题（公式8转换为公式13），再通过EM算法来解决该极大似然估计问题，完成条件生成。以上两步，构成 ft → ft−1 的单次迭代，而最终经过T次迭代后，得到融合图像 f0 。

本文：https://https://arxiv.org/abs/2303.06840
代码：https://github.com/Zhaozixiang1228/MMIF-DDFM

文章题目与作者信息：

DDFM: Denoising Diffusion Model for Multi-Modality Image Fusion

在CVer微信公众号后台回复：DDFM，可以下载本论文pdf、代码

下面是正文部分。

多模态图像融合目的在于组合不同模态下的图像并保留互补信息，为了避免GAN模型诸如训练不稳定和缺少解释性这类问题，同时利用好强大的生成先验，本文提出了基于去噪扩散概率模型 Denoising diffusion probabilistic model (DDPM) 的融合算法。融合任务会在DDPM采样框架下设计为条件生成问题，并被分成无条件生成子问题和最大似然子问题。其中最大似然子问题通过具有隐变量的分层贝叶斯方式建模，并使用期望最大化算法进行推理。通过将推理解决方法整合进扩散采样迭代中，本文方法可以生成高质量的融合图像，使其具备自然的图像生成先验和来自源图像的跨模态信息。需要注意的是本文方法需要无条件预训练生成模型，不过不需要fine-tune。实验表明本文在红外-可见光融合以及医学影像融合中效果很好。

红外-可见光融合IVF就是要避免融合图像对可见光的光照敏感，避免对红外的噪声和低分辨率敏感。基于GAN的融合方法如下图a，会有一个生成器得到融合图像，然后判别器来决定融合图像和哪个模态的源图像更接近。基于GAN的方法容易出现训练不稳定的问题，同时有缺少解释性等问题。另外由于基于GAN的方法是一个黑箱，很难理解GAN的内在机制和行为，让可控的融合变得困难。

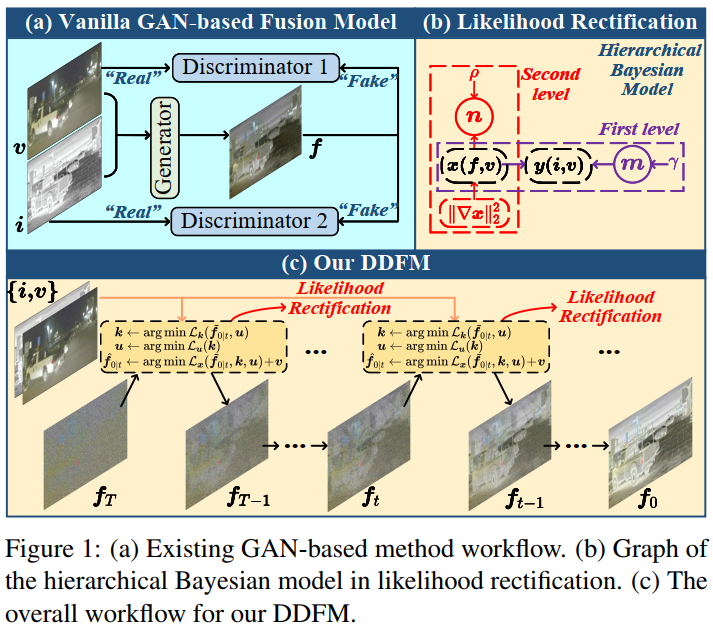
近来去噪扩散概率模型 Denoising diffusion probabilistic model (DDPM)在图像生成中获得很多进步，通过对一张noise-corrupted图像恢复为干净图像的扩散过程进行建模， 可以生成质量很好的图像。基于Langevin扩散过程的DDPM利用一系列逆扩散步骤来生成效果很好的合成图像。对比GAN的方法，DDPM不需要判别器，因此缓解了基于GAN方法诸如训练不稳定和模式崩溃等问题。另外，由于这类方法是基于扩散过程的，所以基于DDPM的生成过程具有可解释性，可以更好地理解图像生成过程。

因此本文提出了 Denoising Diffusion image Fusion Model (DDFM)，其结构如上图的c，本文将条件生成任务设计为基于DDPM的后验采样模型，进一步可以被分为无条件生成扩散问题和最大似然估计问题，第一个问题可以满足自然图像先验，第二个问题通过似然矫正来限制生成图像和源图像之间的相似性。和判别式方法相比，用DDPM对自然图像先验建模可以得到更好的细节生成，这点很难通过损失函数的设计来达到。作为生成模型，DDFM效果稳定，生成效果可控。综合来说本文贡献如下：1.引入基于DDPM的后验采样模型来进行多模态图像法融合任务，包含无条件生成模块和条件似然矫正模块，采样的图像只通过一个预训练的DDPM完成，不需要fine-tune；2.似然矫正中，由于显式获得似然不可行，因此将优化损失表示为包含隐变量的概率推理问题，可以通过 EM 算法来解决，然后这个方法整合进DDPM回路中完成条件图像生成；3.实验表明本文方法在IVF和医学影像融合中都可以获得很好的结果。

Score-based扩散模型：首先看score SDE 方程。扩散模型目标是通过反转一个预定义的前向过程来生成样本，这个前向过程就是将干净的样本 x0 通过多个加噪过程，逐步转换成接近高斯信号的样本 xT ，其过程可以用随机微分方程表示，如下式。

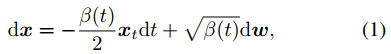
其中 dw 是标准Wiener过程， β(t) 是有利于variance-preserving SDE 的预定义噪声表。

该前向过程可以被反转并保持SDE的形式，如下式。

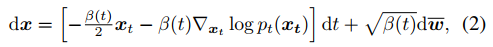
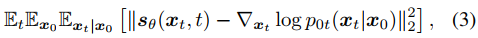
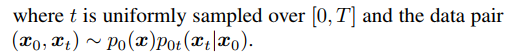
下来是使用扩散模型采样。无条件扩散生成过程从一个随机噪声向量 xT 开始，根据式2的离散化形式进行更新。也可以将DDIM的方式理解采样过程，即score函数可以被看做一个去噪器，在迭代t中，从状态 xt 预测去噪结果 x~0|t ，如下式。

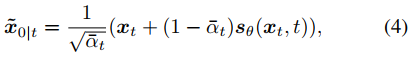
这样 x~0|t 就可以表示给定 xt 时， x0 的估计。

具体更新的方式如下。

使用上面的方式，直到 x0 被生成。

本文基于DDPM和以往方法的对比：传统基于优化的方法主要是收到人工设计损失函数的限制，这可能会让这类方法在数据分布发生改变时融合效果不佳。虽然整合自然图像先验可以提供额外的知识，但是只用损失函数来建模是远远不足的。和GAN方法相比，本文的扩散模型方法可以避免不稳定的训练和模式坍塌，通过每次迭代过程中对源图像生成过程的矫正和基于似然的优化就可以得到稳定的训练和可控融合了。

模型结构

通过扩散后验采样来融合图像：使用i、v、f分别表示红外、可见光、融合图像，其中融合图像与可见光图像均为RGB彩图。期望f的后验分布可以通过i和v建模，这样f就可以通过后验分布中采样得到了。受到式2的启发，扩散过程的逆SDE可以用下式表示。

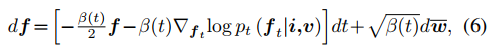
score函数可以通过下式计算。

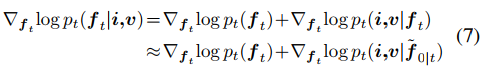
其中 f~0|t 是给定ft后，从无条件DDPM中对 f0 的估计。上式来源于贝叶斯理论，其近似方程可以看原文引用的文献。上式中的第一项表示无条件扩散采样的score函数，可以通过预先训练的 DDPM 轻松推到出来。下一节将解释第二项的获得方式。

图像融合的似然矫正：传统图像退化反转问题，如下式。

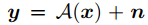
x 是groundtruth， y 是测量方法， A 是已知的，可以显式地获得其后验分布，然后在图像融合问题中，想要在给定 ft 或者 f~0|t 情况下，获得i和v的后验分布是不可能的。为了解决这个问题，首先需要建立优化函数和概率模型的似然之间的关系。下面使用 f 来表示 f~0|t 。

图像融合通常使用的损失函数如下式。

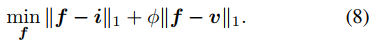
使用x=f-v和y=i-v来替换变量，可以得到下式。

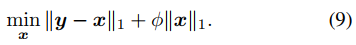
由于y已知，而x未知，那么上式中的第一项就对应于下式k恒为1的回归模型。

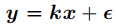
而根据正则项和噪声先验分布之间的关系， ϵ 必须是拉普拉斯噪声，x则是服从拉普拉斯分布。那么根据贝叶斯准则，有下式。

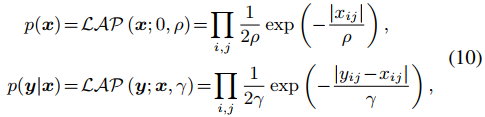
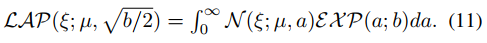
因此式10中的 p(x) 和 p(y|x) 可以被写为下面的分层贝叶斯框架。

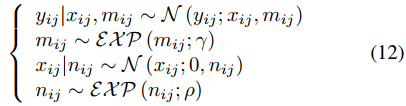
其中i和j分别表示图像的高和宽。通过上式，就可以将式9中的优化问题转换为一个最大似然推理问题。

另外，全变分惩罚项也可以加到融合图像f中，以更好地从可见光图像v中保留纹理信息，其形式如下，先对x求梯度后再计算L2范数。

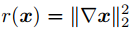
最终，概率推理问题的对数似然函数用下式表示。

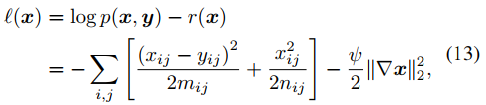
这个分层贝叶斯模型的概率图即为图1的b形式。

这里将式8的优化问题转换为了式13最大似然问题的概率模型。另外和传统方法中人工调整参数惩罚项参数 ϕ 不同，本文方法可以通过推理隐变量，自适应地更新参数 ϕ ，让模型可以更好地拟合不同数据分布。

下面是通过EM算法推理似然模型。为了解决式13的最大对数似然问题，也就是可以被看做包含隐变量的优化问题，本文使用Expectation Maximization, EM算法来获得x。EM步骤如下。

在E步骤中，由下面的命题2来计算隐变量条件期望的计算结果，并得到Q方程的推导。

命题2：隐变量1/m和1/n的条件期望计算如下式，证明过程可以看原文。

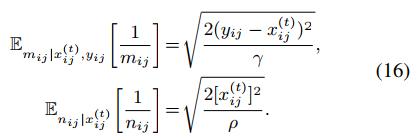
然后，可以通过贝叶斯理论得到m的后验概率，如下。

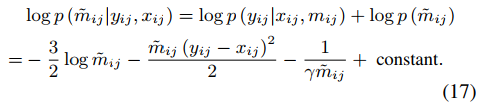
同时m的后验概率可以通过下式计算。

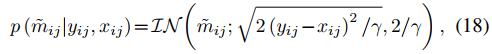
其中IN是逆高斯分布。

对于n也可以用式17相同的方式计算，如下式。

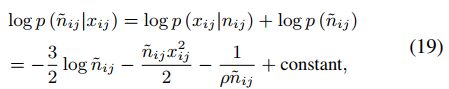
那么n也可以转换为使用逆高斯分布计算的方式，如下式。

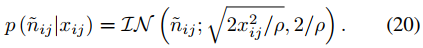
最终，1/m和1/n的条件期望就是式18和20中逆高斯分布的平均参数。

那么Q方程就可以通过下式推到得到。

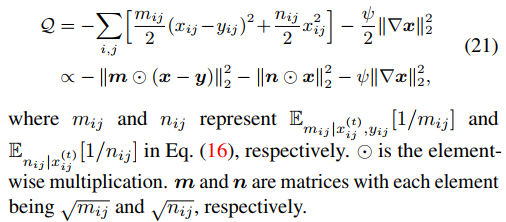
M步骤中，需要最小化关于 x 的负 Q 函数，用half-quadratic splitting算法来处理该问题，如下式。

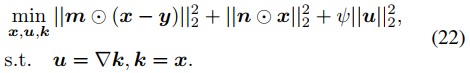
可以进一步转化为如下无约束优化问题。

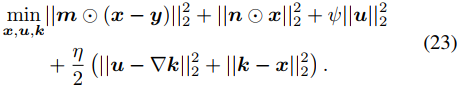
式中的未知变量k、u、 x 可以通过坐标下降方式迭代求解。

k的更新是反卷积过程，如下式。

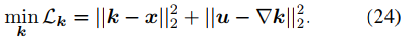
可以采用快速傅里叶变换及其逆变换算子来得到，如下式。

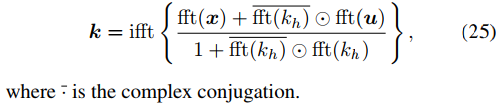
u的更新是L2范数惩罚回归问题，如下式。

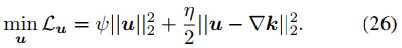
其计算方式如下。

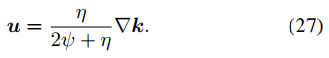
x的更新是最小二乘问题，如下式。

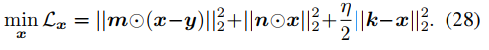
其计算方式如下。

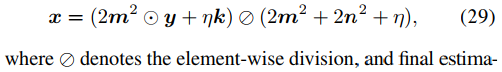
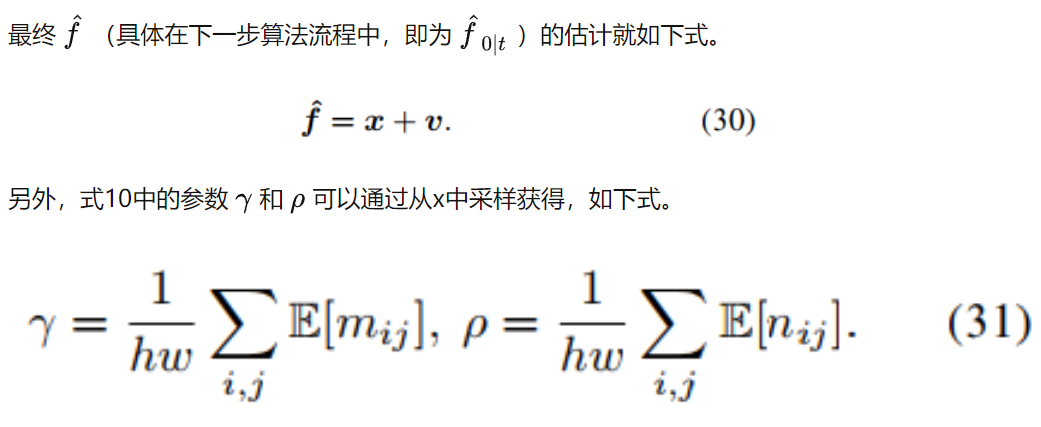
DDFM：前面部分描述是从已有损失函数中获得分层贝叶斯模型，通过EM算法来进行推理。下面讲述本文DDFM将推理方法和扩散采样整合到同一个框架内，根据输入v和i获得融合图像f，算法流程如下。

 

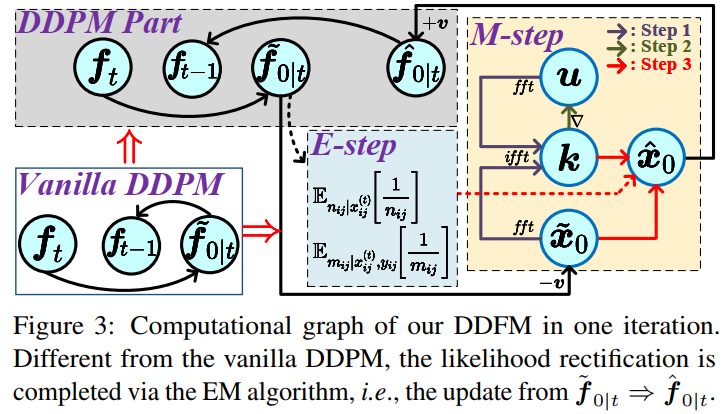
DDFM中包含两个模块，一个是无条件扩散采样模块unconditional diffusion sampling (UDS) ，一个是似然矫正，也就是EM模块。UDS模块用来提供自然图像先验，给融合图像提供较好的视觉效果。EM模块通过似然来保护源图像的更多信息，用于对UDS输出进行矫正。

EM模块用来将 f~0|t 更新为 f^0|t ，在上图算法中对应蓝色和黄色部分。使用DDPM采样（第五行）得到的 f~0|t 作为EM的起始输入，获得 f^0|t （第6到13行），是经过似然校正的融合图像的估计。总体来说，EM模块就是将 f~0|t 更新为 f^0|t 来满足似然。

为什么单步EM可以work：本文DDFM和传统EM算法最大不同就是传统方法需要多部迭代来获得x，也就是上图算法中的第6到13行需要多次循环。本文的DDFM只需要单阶段EM迭代，可以直接嵌入到DDPM框架中完成采样。下面给出命题3来解释这种合理性。

命题3：单步无条件扩散采样结合了单步EM迭代等价于单步有条件扩散采样。下面是证明过程结论。

也就是说，条件采样可以被分为无条件扩散采样和单步EM算法，这就对应了本文的UDS模块和EM模块。

实验部分

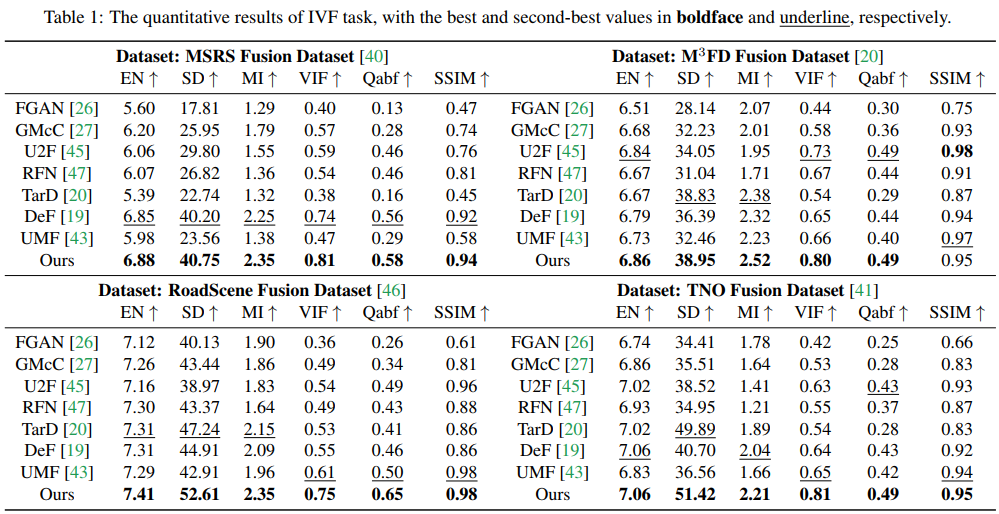
首先是IVF的实验结果。实验在TNO、RoadScene、MSRS、M3FD四个数据集上进行验证，需要注意的是由于本文方法不需要针对特定任务进行fine-tune，所以不需要训练集，直接使用预训练过的DDPM方法即可。本文采用的是在imagenet上预训练的模型。对比实验结果如下。

 

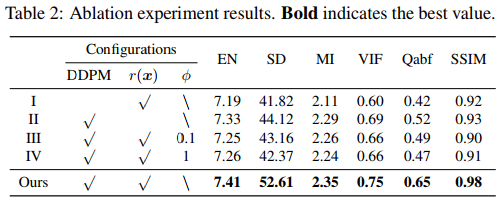
消融实验一个针对UDS模块，一个针对EM模块。对于UDS模块，去掉去噪扩散生成网络，只用EM算法来解决式8的优化问题来获得融合结果（实验I）。为了公平对比，将总体的迭代次数设置的和DDFM相同。EM模块是去除了式13中的总变分惩罚项，然后再去除贝叶斯推理模型（实验II）。而前文也说过式8中的参数 ϕ 可以在分层贝叶斯模型中推理，因此这里将参数 ϕ 分别设置为0.1和1（实验III和IV），使用ADMM来推理模型。以上设置的实验结果如下表。

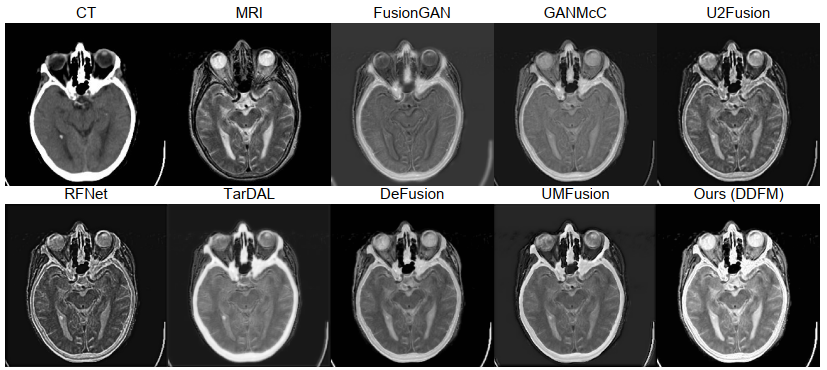
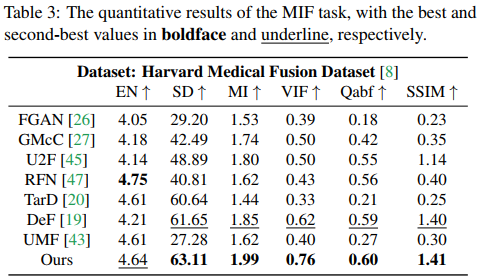
下一组实验是医学影像融合的结果，在 Harvard Medical Image Dataset 上进行测试，包含MRI-CT、MRI-PET、MRI-SPECT三种，实验结果如下图。