10分钟快速了解神经网络（Neural Networks）

Sadaf Saleem | 作者

罗伯特 | 编辑

---

神经网络是深度学习算法的基本构建模块。神经网络是一种机器学习算法，旨在模拟人脑的行为。它由相互连接的节点组成，也称为人工神经元，这些节点组织成层次结构。

 

神经网络与机器学习有何不同？

神经网络是一种机器学习算法，但它们与传统机器学习在几个关键方面有所不同。最重要的是，神经网络可以自行学习和改进，无需人的干预。它可以直接从数据中学习特征，因此更适合处理大型数据集。然而，在传统机器学习中，特征需要手动提供。

---

为什么使用深度学习？

深度学习的一个关键优势是其处理大数据的能力。随着数据量的增加，传统机器学习技术在性能和准确性方面可能变得低效。而深度学习则能够持续表现出色，因此是处理数据密集型应用的理想选择。

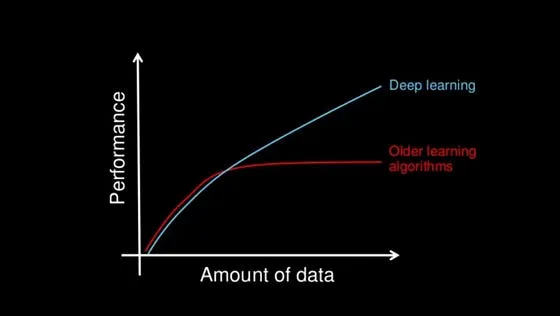
有人会问，为什么我们要费心研究深度学习的结构，而不是简单地依赖计算机为我们生成输出结果，这是一个合理的问题。然而，深入了解深度学习的底层结构可以带来更好的结果，这其中有很多令人信服的理由。

---

研究深度学习结构的好处是什么？

通过分析神经网络的结构，我们可以找到优化性能的方法。例如，我们可以调整层数或节点的数量，或者调整网络处理输入数据的方式。我们还可以开发更适合分析医学图像或预测股市的神经网络。如果我们知道网络中的哪些节点对于特定输入被激活，我们可以更好地理解网络是如何做出决策或预测的。

---

神经网络如何工作？

每个神经元代表一个计算单元，接收一组输入，执行一系列计算，并产生一个输出，该输出传递给下一层。

就像我们大脑中的神经元一样，神经网络中的每个节点都接收输入，处理它，并将输出传递给下一个节点。随着数据在网络中传递，节点之间的连接会根据数据中的模式而加强或减弱。这使得网络可以从数据中学习，并根据其学到的知识进行预测或决策。

想象一个28x28的网格，其中某些像素比其他像素更暗。通过识别较亮的像素，我们可以解读出在网格上写的数字。这个网格作为神经网络的输入。

 

网格的行排列成水平的一维数组，然后转化为垂直数组，形成第一层神经元，就像这样；

 

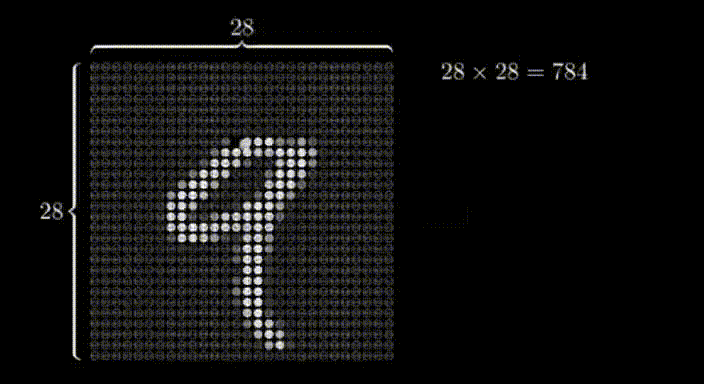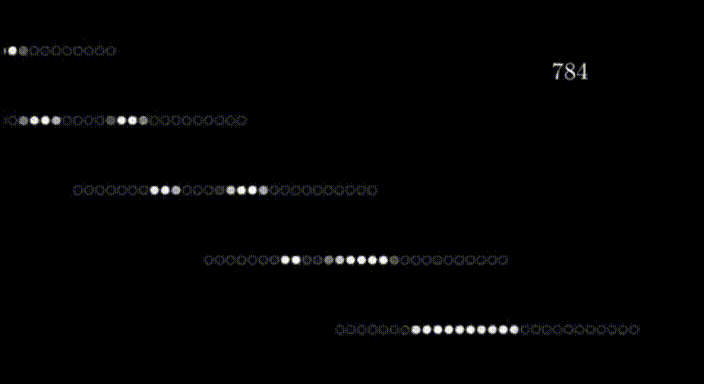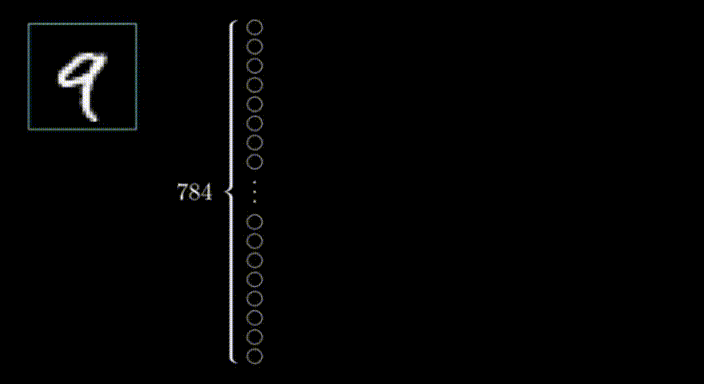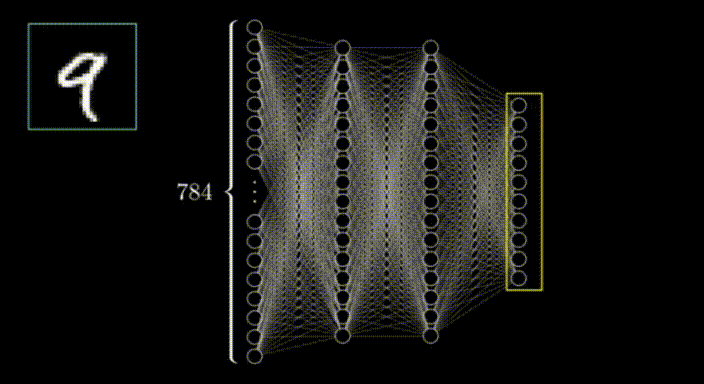
在第一层的情况下，每个神经元对应于输入图像中的一个像素，每个神经元内的值代表该像素的激活或强度。神经网络的输入层负责接收原始数据（在本例中是图像）并将其转化为可以被网络其余部分处理的格式。

在这种情况下，我们有28x28个输入像素，这给了我们784个输入层的神经元。每个神经元的激活值要么是0，要么是1，这取决于输入图像中相应的像素是黑色还是白色。

 

神经网络的输出层在这种情况下包括10个神经元，每个代表一个可能的输出类别（在本例中是数字0到9）。输出层中每个神经元的输出代表输入图像属于该特定类别的概率。最高概率值确定了对于该输入图像的预测类别。

---

隐藏层

在输入层和输出层之间，我们有一个或多个隐藏层，对输入数据执行一系列非线性变换。这些隐藏层的目的是从输入数据中提取对当前任务更有意义的高级特征。您可以决定在网络中添加多少隐藏层。

 

隐藏层中的每个神经元都从前一层的所有神经元接收输入，并在将结果通过非线性激活函数之前，对这些输入应用一组权重和偏差。这个过程在隐藏层的所有神经元上重复，直到达到输出层。

---

前向传播

前向传播是将输入数据通过神经网络生成输出的过程。它涉及计算网络每一层中每个神经元的输出，通过将权重和偏差应用于输入并通过激活函数传递结果来完成。

数学公式：  或   其中，   是神经网络的输出，   是非线性激活函数，  是第   个输入特征或输入变量，   是与第  个输入特征或变量相关联的权重，   是偏差项，它是一个常数值，加到输入的线性组合上。  ：这是输入特征和它们相关权重的线性组合。有时这个术语也被称为输入的“加权和”。

---

反向传播

反向传播是训练神经网络中常用的算法。它涉及计算梯度，即损失函数相对于网络中每个权重的变化的度量。损失函数衡量了神经网络在给定输入下能够正确预测输出的能力。通过计算损失函数的梯度，反向传播允许神经网络以减小训练过程中的整体误差或损失的方式更新其权重。

该算法通过将来自输出层的误差沿着网络的层传播回去，使用微积分的链式法则计算损失函数相对于每个权重的梯度。然后，这个梯度用于梯度下降优化，以更新权重并最小化损失函数。

---

神经网络中使用的术语

神经网络的训练是根据输入数据和期望输出来调整神经网络权重的过程，以提高网络预测的准确性。权重：权重是在训练过程中学到的参数，它们决定了神经元之间连接的强度。每个神经元之间的连接被分配一个权重，该权重与输入值相乘，以确定其输出。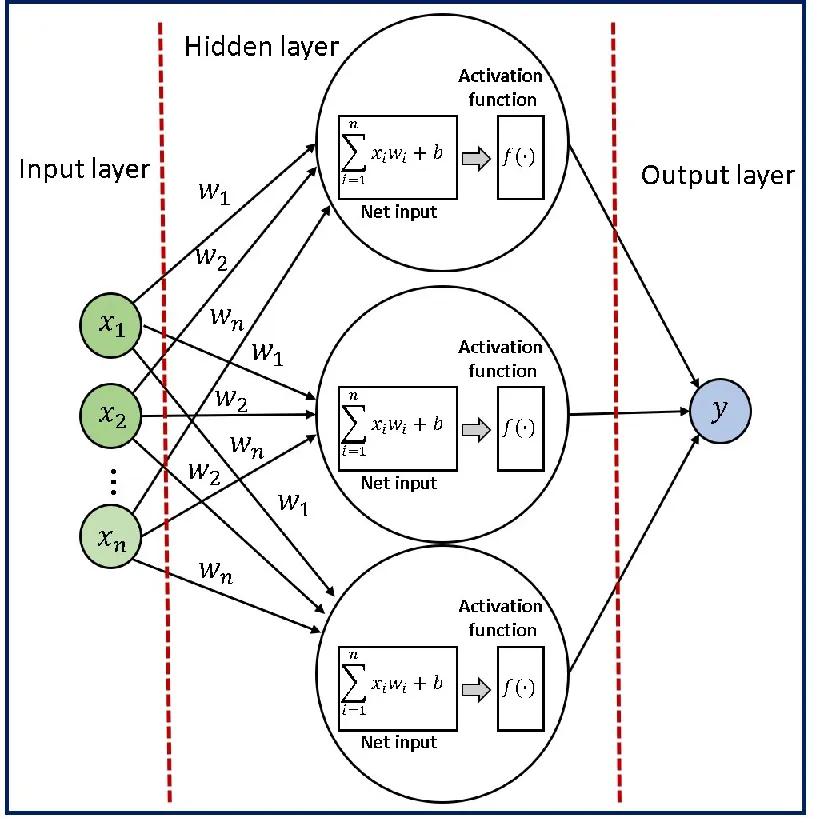

偏差（Bias）：偏差是另一个在给定层中神经元的加权和上添加的学习参数。它是神经元的附加输入，有助于调整激活函数的输出。

非线性激活函数（Non-linear activation function）：非线性激活函数应用于神经元的输出，引入了网络中的非线性。非线性很重要，因为它允许网络建模输入和输出之间的复杂、非线性关系。在神经网络中常用的激活函数包括 Sigmoid 函数、ReLU（修正线性单元）函数和 softmax 函数。损失函数（Loss function）：这是一个数学函数，用于衡量神经网络的预测输出与真实输出之间的误差或差异。经验损失度量了整个数据集上的总损失。交叉熵损失常用于输出概率在0和1之间的模型，而均方误差损失用于输出连续实数的回归模型。目标是在训练过程中最小化损失函数，以提高网络预测的准确性。损失优化（Loss optimization）：这是在神经网络进行预测时，最小化神经网络所产生的误差或损失的过程。这是通过调整网络的权重来完成的。

梯度下降（Gradient descent）：这是一种用于寻找函数最小值的优化算法，例如神经网络的损失函数。它涉及迭代地调整权重，沿着损失函数的负梯度方向。其思想是不断将权重朝着减小损失的方向移动，直到达到最小值。

---

让我们通过实际例子记住这些术语：

1. 想象一家公司希望通过销售产品来最大化利润。他们可能有一个基于各种因素如价格、营销支出等来预测利润的模型。偏差可能指的是影响产品利润但与价格或营销支出无直接关系的任何固定因素。例如，如果产品是季节性物品，可能在一年中的某些时段存在对更高利润的偏差。实际利润与预测利润之间的差异就是损失函数。梯度下降涉及计算损失函数相对于每个输入特征的梯度，并使用这个梯度迭代地调整特征值，直到找到最佳值的过程，而涉及找到最小化损失函数的输入特征的最佳值的过程就是损失优化。利润预测模型可能会使用非线性激活函数将输入特征（例如价格、营销支出）转化为预测的利润值。这个函数可以用来引入输入特征和输出利润之间的非线性关系。2. 想象你正在玩一个视频游戏，你是一个角色试图到达一个目的地，但你只能在二维平面上移动（前后和左右）。你知道目的地的确切坐标，但不知道如何到达那里。你的目标是找到到达目的地的最短路径。在这种情况下，损失函数可以是你当前位置与目的地之间的距离。损失函数的梯度将是通往目的地最陡坡度的方向和大小，你可以使用它来调整你的移动，靠近目的地。随着你靠近目的地，损失函数减小（因为你离目标更近了），梯度也相应改变。通过反复使用梯度来调整你的移动，最终你可以以最短路径到达目的地。希望你在了解神经网络方面有了更深入的了解。为了更好地理解这一概念，请参考文章中提到的视频。