

信号完整性的信号带宽对上升边的影响
电子说
描述
3.1
带宽的定义
带宽用于表示频谱中最高的有效正弦波频率分量值。为了充分近似刻画时域波形的特征, 这是需要包含的最高正弦波频率。所有高于带宽的频率分量都可忽略不计。
带宽这一术语最初在射频领域中用于表示信号的频率范围。在射频应用中,以幅度和相位的形式来调制载波频率,是一种典型的方式。信号中的各频谱分量组成了一个频带。这种射频信号的频率范围就称为带宽。一个射频信号的带宽定义了不同的通道所能传输信号的密集程度。
对于数字信号,带宽同样指的是信号频谱中的频率范围。只不过对于数字信号而言,低频范围起始于直流分量并延伸到最高频率分量。在数字信号领域里,因为最低频率是直流,所以带宽总是对应于最高的有效正弦波频率分量值。
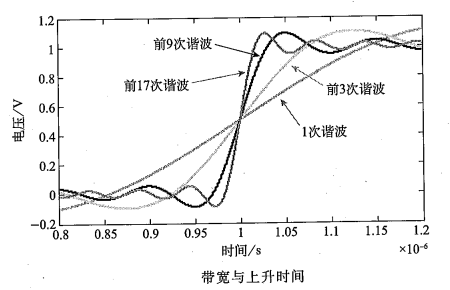
如上图所示,如果只用0次、1次和3次谐波合成时域波形,那么所得波形的带宽只达到3次谐波的值,即3GHz。设计时,这个波形的最高正弦波频率分量是3GHz,其他正弦波频率分量的幅度为零。
如果增加更高次谐波用于生成波形,那么设计的带宽9GHz,17GHz。如果取出图中上升边最短的波形,并把它变换到频域中,则其频谱中含有的谐波分量从0次谐波一直到17次谐波,超过17次谐波的所有分量都为零。这个波形中的最高有效正弦波频率分量就是17次谐波,即此波形的带宽为17GHz。
3.2
带宽对上升边的影响
第二章已经说明了由信号的频谱可以得到时域波形,实质上是傅里叶逆变换过程,只不过对于周期信号来说,这一傅里叶逆变换过程更明显地表现为一系列单频信号的加权和的形式。
对于理想方波信号,上升时间为0,每一个频率分量都是必需的,因此,理论上理想方波信号带宽是无穷大的。尽管如此,无穷大的带宽对实际工程应用没有什么实际意义,信号频谱中各个频率分量的贡献是不同的。
我们已经知道了频率趋于无穷大时方波信号的频谱幅度以一20 dB/十倍频程的速度衰减,对于某个频率分量,如果其频谱幅度足够小,以至于我们可以把它对波形的贡献忽略掉,那么我们就可以不必考虑它的影响,这就是定义信号带宽的根本原因。
使用有限带宽的频谱来代替无穷宽的频谱,进而得到一个对原信号的可接受的近似,对工程应用更具有实际意义。
通过仿真实验分析信号频谱中各个频率分量是如何影响信号时域波形的。
下图是理想方波的级数展开式:

下图分别是1f、3f、11f、39f 带宽的波形图


至此,我们得到结论:上升时间越小,信号带宽越大,说明高频成分对信号的贡献越大。如果信号上升时间较长,使用相对较小的带宽就可以合成信号波形,说明高频成分的贡献要小得多。反映在频谱上,高频成分的频谱幅度相对较小,因此,上升时间越长,频谱中高频成分衰减越快。
带宽和上升时间的关系:

3.3
时钟频率与带宽
众所周知,带宽与信号的上升边直接有关。我们并非总能知道信号的上升边,但是却需要知道它的带宽。若给定一个简单的假设,就可以从信号的时钟频率估算出它的带宽。需要注意的是,不是时钟频率而是上升边决定带宽。
为了通过信号的时钟频率估计它的带宽,必须做一个非常重要的假设,即首先估计出时钟波形典型的上升边。如果不知道上升边与周期的比值,则一个合理的概括是:上升边是时钟周期的7%。
这与许多微处理器板和ASIC驱动板级总线的情况接近。因此,可以据此估算时钟波形的带宽。即带宽是时钟频率的5倍:BW_clock= 5 x F_clock。或者说,时钟波形中典型的最高正弦波频率分量就是5次谐波。
-
听懂什么是信号完整性2024-12-15 1128
-
何为信号完整性?信号完整性包含哪些2021-12-30 2769
-
信号完整性与电源完整性的仿真2021-09-29 1511
-
信号完整性对EMC的影响有哪些2020-07-09 4235
-
基于PCB信号完整性的反射设计2017-11-09 955
-
【下载】《信号完整性与电源完整性分析》——高速PCB人员的必备书籍,EMI经典之作2017-08-08 67056
-
信号完整性小结2015-12-12 3630
-
信号完整性分析2015-11-10 1002
-
信号完整性与电源完整性仿真分析2011-11-30 2000
-
2011信号及电源完整性分析与设计2010-12-16 3484
-
信号完整性基础指南2010-08-05 1157
-
信号完整性原理分析2009-11-04 1203
-
高速电路信号完整性分析与设计—信号完整性仿真2009-10-06 1541
-
什么是信号完整性2009-06-30 5711
全部0条评论

快来发表一下你的评论吧 !

