

电感如何优化物理设计以得到合格的信号完整性呢?
电子说
描述
8.1
电感的定义
电感是一个非常重要的电气参数,因为它影响几乎所有的信号完整性问题。对于线间耦合、电源分配网络及电磁干扰问题,电感就是信号沿均匀传输线传播过程中遇到的突变。
很多场合都要设法减小电感,例如减小信号路径之间的互感以降低开关噪声,减小电源分配网络的回路电感,减小返回平面的有效电感以降低电磁干扰。而有些场合则要优化电感,例如为了获取所需的目标特性阻抗。
通过了解电感的基本类型和物理设计对电感值的影响,将领会如何优化物理设计以得到合格的信号完整性。
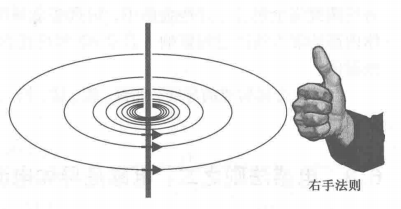
通电导线的周围都存在磁力线圈。想象沿着导线行走,并计算完全围绕住导线的磁力线匝数。距离电流表面越远,所见到的磁力线匝数就越少。
磁力线圈总是完整的环形,而且总是包围着某一电流。电流周围一定存在磁力线圈。
电感是当导体通过单位安培电流时其周围磁力线匝数的度量,即 L = N/I ,若流过导体的电流加倍,则磁力线匝数也会加倍,但二者比值不变,且该比值与流过导体的电流完全无关。所以,无论导体中的电流是0A还是100A,其电感都是一样的。
同理,当磁力线匝数改变时,表示这一比值的电感依然不变。这说明电感实际上与导体的几何结构有关。影响电感的唯一因素就是导体的几何结构和在铁磁金属情况时导体的磁导率。
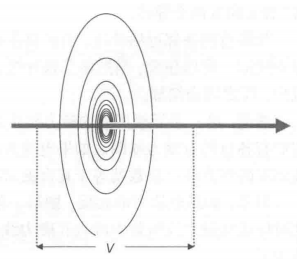
磁力线圈有一个重要的特殊性质:无论什么原因,只要一段导线周围的磁力线匝总数发生变化,导线两端就会产生一个感应电压。如上图所示,该电压与磁力线匝总数变化的快慢有着直接关系:V = ∆N/∆t 。
如果导线中的电流发生变化,则其周围的自磁力线匝数也将变化,从而在导线两端产生电压。导线周围的磁力线匝数为 N = LI, 其中L是这段导线的自感。所以导线两端所产生的电压(感应电压)与导线的电感和导线中电流变化的快慢有关,即:
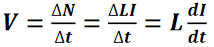
这种关系就是电感器的一种定义。如果通过电感器的电流发生变化,电感器两端就会产生电压,这一电压被称为感应电动势。这一新的电压源像电池一样引发了从负端流向正端的电流。该电压的极性将使产生的感应电流阻碍原电流的变化。这就是我们说“电感器阻止电流变化”的原因。
感应电压正是电感在信号完整性中意义重大的根本原因。如果电流变化时没有产生感应电压,信号就不会受到电感的影响。这个由电流变化产生的感应电压引起了传输线效应、突变、串扰、开关噪声、轨道塌陷、地弹和大多数电磁干扰源。
如果一条导线附近的另一条导线中有电流,则第二条导线的一些磁力线圈同时也环绕住第一条导线。那么第二条导线中的电流变化时,在第一条导线周围的那部分磁力线匝数也将发生变化,这个变化的磁力线匝数使第一条导线两端产生感应电压,互磁力线匝数的变化在第一条导线的两端产生了感应电压。通常,另一条导线中的电流发生变化时,我们用串扰描述在邻近导线上产生的感应电压噪声。在这种情况下,产生的电压噪声为:

其中,V_noise表示第一条导线a中的感应电压噪声,M表示两条导线之间的互感(单位为Wb),I表示第二条导线b中的电流。
由于感应电压取决于电流变化的速率,所以有时用开关噪声或△I噪声描述当电流切换时在电感上产生的噪声。
8.2
自感和互感

两条邻近的导线a和b,如果只有a中有电流,其周围就会有磁力线圈和电感。假如在第二条导线b中也有电流,则其周围也会有磁力线圈,从而也具有电感。由导线b产生的部分磁力线圈也将环绕住第一条导线a。因此对于a而言,环绕在它周围的磁力线圈的一部分由其自身的电流产生,一部分由邻近第二条导线b的电流产生。
当计算一条导线周围的磁力线圈时,需要有一种方式表明磁力线圈的源头。我们把一条导线自身电流产生的磁力线圈称为自磁力线圈,把由邻近电流产生的磁力线圈称为互磁力线圈。
自感是指导线中流过单位安培电流时,所产生的环绕在导线自身周围的磁力线匝数。通常我们所说的电感实际上是导线的自感。导线的自感与其他导线的电流是无关的。如果把另一条通有电流的导线靠近第一条导线,则第一条导线周围的磁力线匝总数会发生变化,但其自身电流产生的磁力线匝数是不变的。
互感是指一条导线中流过单位安培电流时,所产生的环绕在另一条导线周围的磁力线匝数。把两条导线拉近时,它们的互感会增大,反之则会减小。
互感有两个不同寻常的微妙特性。
第一,互感具有对称性。无论是在第一条导线中加单位安培电流去测量第二条导线周围的磁力线匝数,还是在第二条导线中加单位安培电流去测量第一条导线周围的磁力线匝数,得到的结果都是相同的。从这方面讲,互感与链接到两条导线的磁力线圈有关,并且它与这两条导线的关系是同等的,即这个特性是两条导线共有的,所以有时把互感称为“两条导线之间的互感”。无论每条导线的形状和大小怎样,上述这个结论都是正确的。两条导线的几何结构可以不同,如一条可以是窄导线,另一条则可以是宽平面。但无论是在宽导线还是在窄导线中加入单位安培电流,去计算另一条导线周围的磁力线匝数,其结果是相同的。
第二,两条导线之间的互感小于二者中任一个的自感。毕竟,每条互磁力线圈都源于某一导线并且一定是某一导线的自磁力线圈,而且两条导线之间的互感与在哪条导线中加电流无关,所以互感一定小于两条导线的自感的最小值。
8.3
局部电感
在计算磁力线圈时,由于仅考虑了导线中电流回路的一部分,且假设回路的其他部分不存在电流,所以把这种电感称为局部电感。当谈到局部电感时,认为回路的其他部分是不存在的。从局部电感的角度出发,除了所研究的那段导体,其他地方没有电流。局部电感的概念是一个纯粹的数学构造,它是不可测量的,因为实际中并不存在孤立的局部电流。但局部电感的概念对于理解和计算电感的相关特征非常有用,尤其当我们还不清楚回路其他部分的情况时很有用。
局部电感分为局部自感和局部互感。局部自感和局部互感的准确定义是以对某一段导线周围磁力线匝数的数值计算为依据的。从电流回路中选取一段给定长度的导线,假设这段导线在空间中是孤立的,但仍保持其原来的几何结构。在它的两端放置与其相垂直的大块平板。现在想象着注入1A电流,即电流在导线的一端突然出现,并沿导线传播,然后从另一端出来并且突然消失得无影无踪。
实际仅存的电流在双端平面之间的导线段中,由这一小段电流可以计算出双端平面的磁力线匝数。当导线中的电流是1A时,计算出的磁力线匝数就是该段导线的局部自感。
如果在第一段导线附近放置另一段导线,并从这第二段导线的一端注入1A电流,此电流从另一端消失。此时,这部分电流在整个空间内产生磁力线圈,其中一部分线圈出现在第一段导线的双端平面之间,并完全环绕住第一段导线。环绕在第一段导线周围的磁力线匝数就是两段导线之间的局部互感。
局部自感的一个重要特性:电流分布越扩散开,局部电感就越小。反之,电流分布越密集,局部电感就越大。
两段导线之间的局部互感,就是源于其中一条导线并完全环绕在另一条导线周围的磁力线匝数。一般而言,两条导线之间的局部互感仅是其各自局部自感的一小部分,而且一旦两条导线的距离拉大,互感就会迅速减小。
经验法则:当两个导线段的间距远大于导线长度时,两段导线之间的局部互感小于任一段导线局部自感的10%,这时局部互感通常可忽略不计。
8.4
总电感

如图所示,导线中有一段是直的,然后自己又折回,组成一个完整的回路。在所有的互连中,这种结构是很常见的,包括信号路径与返回路径、电源路径与地返回路径。封装中相邻的电源和地返回键合线是常见的示例,在集成电路封装中可能是相邻的信号引脚和返回引脚对,而在电路板上可能是相邻的信号平面和返回平面对。
当回路中有电流流过时,每个支路都会产生磁力线圈。如果回路的电流发生变化,那么这两段导线周围的磁力线匝数都会随之变化。同理,在每个支路两端都会产生一个感应电压,此电压取决于支路周围磁力线匝数变化的快慢。
一条支路周围的磁力线圈由该支路中电流产生的磁力线圈(局部自磁力线圈)和其他支路产生的磁力线圈(局部互磁力线圈)两部分组成。但是,由两个支路产生的磁力线圈方向相反,所以这段回路周围的磁力线匝总数就是自磁力线匝数和互磁力线匝数的差值。当电流为1A时,某支路周围的磁力线匝总数有一个专用名称,即有效电感、总电感或净电感。
以支路b为例,磁力线圈一部分源于支路b的电流,即自磁力线圈。支路b周围,其自身电流的磁力线匝数为:

同时,支路b有些磁力线是源于支路a电流的互磁力线圈,其匝数为:
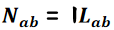
所以互磁力线的方向与支路b的自磁力线方向相反。于是,计算支路b周围的磁力线匝总数时,应将这组磁力线匝数相减,

(L_b −L_ab)为支路b的总电感,它是指回路中电流为单位安培时,支路b周围的磁力线匝总数,其中包括整个回路中所有电流段的影响。当相邻电流的方向相反时,如回路的两条支路中的一条是另一条的返回电流路径时,有效电感决定了回路电流变化时支路两端感应电压的大小。如果这第二条支路是返回路径,则称在该返回路径上产生的电压为地弹。
返回路径上的地弹电压降为:
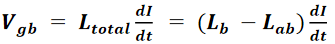
最小化返回路径上的电压降(即地弹电压)只有两种方法。第一种方法,尽可能减小回路电流的变化速率。这意味着降低边沿变化率,并限制共用同一个返回路径的信号路径数目,以及使用差分信令。我们很少有机会去这样做,但是应该经常考虑到这一点。
第二种方法,尽可能减小 L_total。减小返回路径总电感的要点有两方面:减小返回支路的局部自感,增大两支路之间的局部互感。减小返回支路的局部自感意味着使返回路径尽可能短、尽可能宽(也就是使用平面);增大返回路径和初始路径之间的互感则意味着使第一条支路与其返回路径尽可能地靠近。
很明显,减小地弹不仅要在返回路径上采取措施,还要考虑信号电流路径的布局和由此产生的与返回路径之间的局部互感。
运用前面的近似,通过拉近相邻键合线的间距,可以估计键合线的总电感能够减少的程度。假设一条键合线中流过的是电源电流,其他键合线中流过的是地返回电流,即它们中的电流大小相等,方向相反。在这种情况下,键合线之间的局部互感就会使任意一条键合线的总电感减小,即: L_total = (L_a −L_ab) ,并且键合线距离越近,导线之间的互感就越大,任意一条键合线的总电感减小程度也就越大。说明了一个非常重要的设计规则:尽可能让返回电流挤近信号电流,这样可以减小有效电感。
考虑另一种情况,两条导线里流过的都是电源电流。这种情况在许多集成电路封装中十分常见,因为常常使用多条引脚传输电源电流和地电流。那么如果一条电源导线附近还有另一条电源导线,在这种情况下,电流方向相同,互磁力线圈和自磁力线圈方向相同,二者是相叠加的,所以其中一条电源导线的净电感为 L_total = (L_a +L_ab), 为了减小电源引线的净电感,通常就要尽可能地减小引线的局部自感。然而,在这种情况下,由相邻引线产生的磁力线方向相同,所以还必须尽可能地减小引线之间的局部互感。换言之,导线的间距要尽可能大。
只要两条导线的间距大于它们的长度,净电感就和各自的局部自感相差无几。当导线相互靠近时,若其中的电流方向相反,净电感就会减小;若其中的电流方向相同,净电感就会增大。
在电源分配系统中,减小任意一条支路净电感的常用设计规则是:尽可能让同向平行电流之间的间距大于它们的长度。
在大功率芯片中,实际常用的是双键合线,即在一个裸芯片焊盘和对应的封装焊盘之间使用两条键合线。由于这两条键合线是并联的,两个焊盘之间的串联阻抗就降低了。并且与仅用单条键合线相比,这两条键合线的等效电感也就减小了。导线靠得越近,互感就越大,有效电感也就越大。但是,由于这两条导线是并联的,等效电感只是其中任意一条导线的净电感的一半。
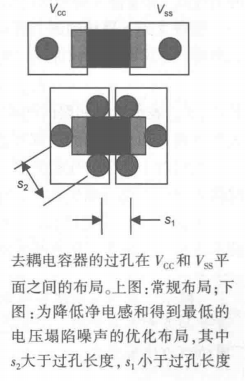
如上图,过孔是从去耦电容器焊盘到下面的电源和地平面的,假设与平面的距离为20 mil,过孔直径为10 mil。那么每个电容器焊盘使用多个并联的过孔是否有好处呢?
如果过孔之间的中心距s大于过孔的长度,即s>20 mil,则局部互感就非常小,而且相互之间几乎没有影响,每个过孔的净电感就等于各自的局部自感。但是,如果从焊盘到下面的平面之间有多个过孔并联,则等效电感就会减小,并与过孔数呈相反的关系,即并联的过孔数目越多,等效电感就越小。同理,若过孔的电流方向相反,则两个过孔靠得越近,每个过孔的有效电感就越小。如果s<20 mil,则每个过孔的净电感将降低,从而焊盘到平面之间的等效电感和轨道塌陷电压也会减小。
在同一焊盘中有多个过孔的另一个重要优点是,由于与电源、地平面的接触面积加大,进入电源、地平面的扩散电感将会减小。有时,这一点比减小过孔电感的效果更重要。
采用下述设计规则可以使每条支路的净电感最小:电流方向相同的过孔之间的中心距应大于过孔的长度,电流方向相反的过孔之间的中心距应小于过孔的长度。
-
pcb信号完整性详解2023-09-08 2254
-
如何利用全新互连系统提高电源完整性和信号完整性?2023-08-30 1784
-
何为信号完整性?信号完整性包含哪些2021-12-30 2769
-
详解信号完整性与电源完整性2021-11-15 2436
-
信号完整性与电源完整性的仿真2021-09-29 1511
-
回流又是如何影响信号完整性的呢?2019-07-11 7177
-
信号完整性 & 电源完整性 谁更重要呢?2019-06-17 2373
-
电地完整性、信号完整性分析导论2016-02-22 1153
-
信号完整性分析2015-11-10 1002
-
信号完整性与电源完整性的仿真分析与设计2015-01-07 6764
-
信号完整性与电源完整性仿真分析2011-11-30 2000
-
信号完整性原理分析2009-11-04 1203
-
什么是信号完整性2009-06-30 5711
全部0条评论

快来发表一下你的评论吧 !

