

浅谈图像处理-harris角点检测算法
电子说
描述
通常意义上来说,角点就是极值点,即在某方面属性特别突出的点,是在某些属性上强度最大或者最小的孤立点、线段的终点。 对于图像而言,其是物体轮廓线的连接点。
1 harris角点检测算法思想
算法的核心是利用局部窗口在图像上进行移动,判断灰度是否发生较大的变化。如果窗口内的灰度值(在梯度图上)都有较大的变化,那么这个窗口所在区域就存在角点。
这样就可以将 Harris 角点检测算法分为以下三步:
1,当窗口(局部区域)同时向 x (水平)和 y(垂直) 两个方向移动时,计算窗口内部的像素值变化量 E(x,y);
2,对于每个窗口,都计算其对应的一个角点响应函数 R;
3,然后对该函数进行阈值处理,如果 R>threshold,表示该窗口对应一个角点特征。
2
建立数学模型
第一步是通过建立数学模型,确定哪些窗口会引起较大的灰度值变化。让一个窗口的中心位于灰度图像的一个位置(x,y),这个位置的像素灰度值为I(x,y),如果这个窗口分别向 x和 y 方向移动一个小的位移u和v,到一个新的位置 (x+u,y+v),这个位置的像素灰度值就是I(x+u,y+v)。|I(x+u,y+v)−I(x,y)|就是窗口移动引起的灰度值的变化值。
设w(x,y)为位置(x,y)处的窗口函数,表示窗口内各像素的权重,最简单的就是把窗口内所有像素的权重都设为1,即一个均值滤波核。当然,也可以把 w(x,y)设定为以窗口中心为原点的高斯分布,即一个高斯核。

如果窗口中心点像素是角点,那么窗口移动前后,中心点的灰度值变化非常强烈,所以该点权重系数应该设大一点,表示该点对灰度变化的贡献较大;而离窗口中心(角点)较远的点,这些点的灰度变化比较小,于是将权重系数设小一点,表示该点对灰度变化的贡献较小。
则窗口在各个方向上移动(u,v)所造成的像素灰度值的变化量公式如下:
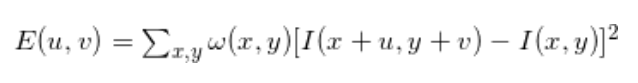
若窗口内是一个角点,则E(u,v)的计算结果将会很大。为了提高计算效率,对上述公式进行简化,利用泰勒级数展开来得到这个公式的近似形式。
对于二维的泰勒展开式公式为:
T(x,y)=f(u,v)+(x−u)fx(u,v)+(y−v)fy(u,v)+....
则I(x+u,y+v) 为:
I(x+u,y+v)=I(x,y)+uIx+vIy
其中Ix和Iy是I的微分(偏导),在图像中就是求x 和 y 方向的梯度图:
Ix=∂I(x,y)/∂x
Iy=∂I(x,y)/∂y
将I(x+u,y+v)=I(x,y)+uIx+vIy代入E(u,v)可得:
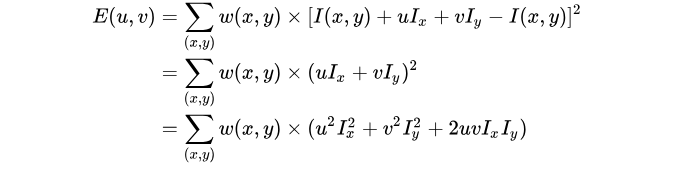
提出 u 和 v ,得到最终的近似形式:
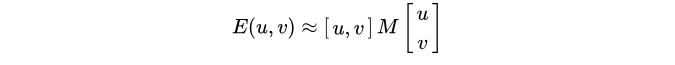
其中矩阵M为:
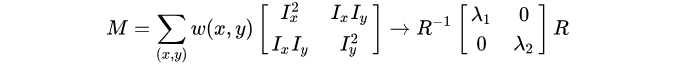
最后是把实对称矩阵对角化处理后的结果,可以把R看成旋转因子,其不影响两个正交方向的变化分量。经对角化处理后,将两个正交方向的变化分量提取出来,就是 λ1 和 λ2(特征值)。
这里利用了线性代数中的实对称矩阵对角化的相关知识,有兴趣的同学可以进一步查阅相关资料。
3
角点响应函数R
现在我们已经得到E(u,v)的最终形式,别忘了我们的目的是要找到会引起较大的灰度值变化的那些窗口。
灰度值变化的大小则取决于矩阵M,M为梯度的协方差矩阵。在实际应用中为了能够应用更好的编程,所以定义了角点响应函数R,通过判定R大小来判断像素是否为角点。
计算每个窗口对应的得分(角点响应函数R定义):
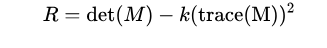
其中 det(M)=λ1λ2是矩阵的行列式,trace(M)=λ1+λ2是矩阵的迹。λ1和 λ2是矩阵M的特征值,k是一个经验常数,在范围 (0.04, 0.06) 之间。R的值取决于M的特征值,对于角点∣R∣很大,平坦的区域∣R∣很小,边缘的R为负值。
4
角点判定
根据 R 的值,将这个窗口所在的区域划分为平面、边缘或角点。为了得到最优的角点,我们还可以使用非极大值抑制。
注意:Harris 检测器具有旋转不变性,但不具有尺度不变性,也就是说尺度变化可能会导致角点变为边缘。想要尺度不变特性的话,可以关注SIFT特征。
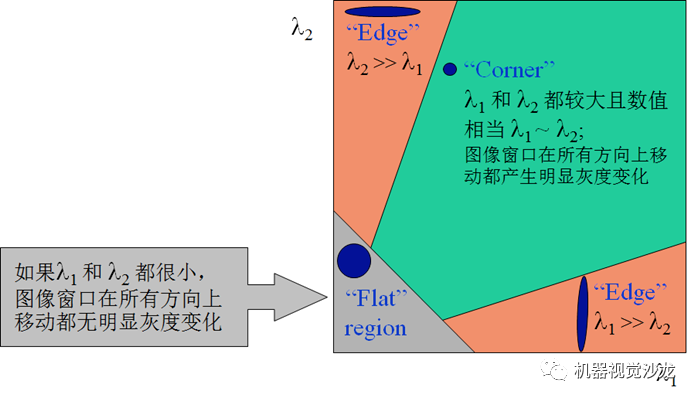
因为特征值 λ1 和 λ2 决定了 R 的值,所以我们可以用特征值来决定一个窗口是平面、边缘还是角点:
平面:该窗口在平坦区域上滑动,窗口内的灰度值基本不会发生变化,所以∣R∣ 值非常小,在水平和竖直方向的变化量均较小,即 Ix和 Iy都较小,那么 λ1 和 λ2 都较小;
边缘:∣R∣值为负数,仅在水平或竖直方向有较大的变化量,即 Ix和Iy只有一个较大,也就是 λ1>>λ2 或 λ2>>λ1;
角点:[公式] 值很大,在水平、竖直两个方向上变化均较大的点,即 Ix和 Iy都较大,也就是 λ1 和 λ2 都很大。
如下图所示:
Harris 角点检测的结果是带有这些分数 R 的灰度图像,设定一个阈值,分数大于这个阈值的像素就对应角点。
编辑:黄飞
-
基于FPGA的图像角点检测2012-04-10 4321
-
人脸检测算法及新的快速算法2013-09-26 3866
-
基于matlab的图像处理--飞机检测2015-09-30 15784
-
机器视觉图像处理之角点检测技术2016-01-22 4302
-
【DragonBoard 410c试用体验】 之OpenCV中之图像角点检测实现2016-09-13 12689
-
基于图像距离差的织物疵点检测算法2009-05-27 596
-
基于小波变换多尺度Harris角点检测算法2010-01-09 678
-
Harris角点特征的图像拼接方法2011-12-29 1194
-
Harris角点检测2016-06-06 535
-
OpenCV3编程入门-源码例程全集-Harris角点检测2016-09-18 486
-
免费下载!一款基于Zynq的Harris角点检测算法实现Demo2017-02-08 628
-
Harris角点检测在列车滑动监测系统中的应用_潘峥嵘2017-03-19 921
-
OpenCV3.1教程之Harris角点检测的详细课件免费下载2020-01-06 851
-
基于高斯金字塔图像的改进Harris特征点检测算法2021-05-06 1030
-
基于Delaunay三角剖分的空间离群点检测算法研究2023-10-07 436
全部0条评论

快来发表一下你的评论吧 !

