如何实现三角波调频电路的设计与模拟呢？

由于调频技术的诸多优点，如调频信号是恒包络信号可以使用效率较高的C类功率放大器，抗干扰性能好，信噪比高等，在当前的移动通信系统中，调频（FM）仍然是最普遍应用的模拟调制技术，各种调频器仍有广泛的应用前景。

本文针对这一问题，首先介绍了不同的调制技术，并对调频技术做了细致讨论；其次分析了三种不同的实现三角波调频的方案，且就其中一种做了深入推导和讨论，并设计出具体的电路；接着，在仿真软件Multisim 10.0环境下，对所设计的三角波调频电路进行了模拟并完成了各种数据和波形的测试；最后，对在电路设计和模拟过程中遇到的各种问题进行了总结。

各种仿波形及数据表明，该电路工作稳定能实现三角波调频，且输出电压稳定、幅度较大，具有一定的应用前景。

1.1调制技术

调制技术就是把低频分量丰富的不适合直接在信道中传输的基带信号变换成适合在信道中传输的高频信号的技术。基带信号是原始的电信号，在数字通信中则指相应的电脉冲。在无线遥测遥控系统和无线电技术中调制就是用基带信号控制高频载波的参数（振幅、频率和相位），使这些参数随基带信号变化。用来控制高频载波参数的基带信号称为调制信号。未调制的高频电振荡称为载波（可以是正弦波，也可以是非正弦波，如方波、脉冲序列等）。被调制信号调制过的高频电振荡称为已调波或已调信号。已调信号通过信道传送到接收端，在接收端经解调后恢复成原始基带信号。解调是调制的反变换。用基带信号调制高频载波，在无线电传输中可以减小天线尺寸，并便于远距离传输。应用调制技术，还能提高信号的抗干扰能力。

调制方式按照调制信号的性质分为模拟调制和数字调制两类；按照载波的形式分为连续波调制和脉冲调制两类。模拟调制有调幅(AM)、调频(FM)和调相(PM)。数字调制有振幅键控（ASK）、移频键控(FSK)、移相键控(PSK)和差分移相键控(DPSK)等。脉冲调制有脉幅调制(PAM)、脉宽调制（PDM）、脉频调制（PFM）、脉位调制(PPM)、脉码调制(PCM)和增量调制（ΔM）。

按照传输特性，调制方式又可分为线性调制和非线性调制。广义的线性调制，是指已调波中被调参数随调制信号成线性变化的调制过程。狭义的线性调制,是指把调制信号的频谱搬移到载波频率两侧而成为上、下边带的调制过程。此时只改变频谱中各分量的频率，但不改变各分量振幅的相对比例，使上边带的频谱结构与调制信号的频谱相同，下边带的频谱结构则是调制信号频谱的镜像。狭义的线性调制有调幅(AM)、抑制载波的双边带调制(DSB)和单边带调制(SSB)。

调制的实质是频谱的搬移，其作用和目的是：①将调制信号（基带信号）转换成适合于信道传输的已调信号（频带信号）；②实现信道的多路复用，提高信道利用率；③减少干扰，提高系统抗干扰能力；④实现传输带宽与信噪比之间的互换。因此，调制对通信系统的有效性和可靠性有很大影响。

模拟调制指调制信号和载波都是连续波的调制方式。它有调幅、调频和调相三种基本形式。调幅(AM)：用调制信号控制载波的振幅，使载波的振幅随着调制信号变化。已调波称为调幅波。调幅波的频率仍是载波频率，调幅波包络的形状反映调制信号的波形。调幅系统实现简单,但抗干扰性差,传输时信号容易失真。调频(FM)：用调制信号控制载波的振荡频率，使载波的频率随着调制信号变化。已调波称为调频波。调频波的振幅保持不变，调频波的瞬时频率偏离载波频率的量与调制信号的瞬时值成比例。调频系统实现稍复杂，占用的频带远较调幅波为宽，但抗干扰性能好，传输时信号失真小，设备利用率也较高。调相(PM)：用调制信号控制载波的相位，使载波的相位随着调制信号变化。已调波称为调相波。调相波的振幅保持不变，调相波的瞬时相角偏离载波相角的量与调制信号的瞬时值成比例。在调频时相角也有相应的变化，但这种相角变化并不与调制信号成比例。在调相时频率也有相应的变化，但这种频率变化并不与调制信号成比例。

在模拟调制过程中已调波的频谱中除了载波分量外在载波频率两旁还各有一个频带，因调制而产生的各频率分量就落在这两个频带之内。这两个频带统称为边频带或边带。位于比载波频率高的一侧的边频带，称为上边带。位于比载波频率低的一侧的边频带，称为下边带。

本文中讨论的三角波调频电路就是将信息寄托在三角波的频率中，使三角波的频率随调制信号变化而幅度保持恒定的一种模拟调频方式。

1.2调频波及调频方法

在图1.1中，正弦波为调制信号，三角波为调频信号。当调制信号最大时，波形密集，当最小时，波形最稀疏，调频波的瞬时频率偏离载波频率的量与调制信号的瞬时值成比例。因此调频波是波形疏密变化的等幅波。调频是将消息寄载在频率上，也可以说调频信号中消息是蕴藏于单位时间内波形数目或者说零交叉点数目中。由于各种干扰足以主要表现在振幅上，而在调频系统中，可以通过限幅器来消除这种干扰，因此FM波抗干扰能力较强。

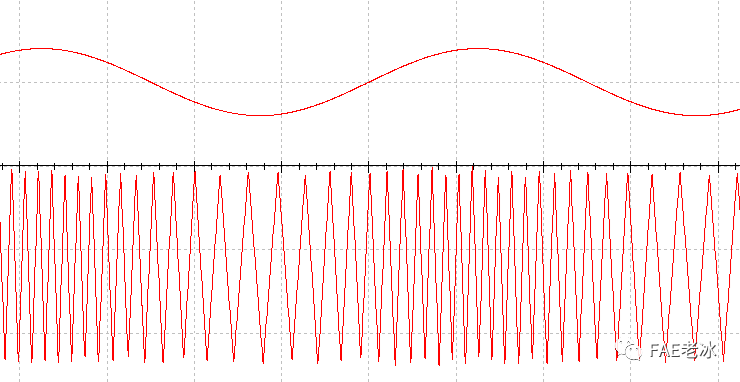
图1.1 调制信号与调频信号波形对比

调频方法分类

1. 直接调频法

这种方法一般是用调制电压直接控制振荡器的振荡频率，使振荡频率按调制电压的规律变化。若被控制的是LC振荡器，则只需控制振荡回路的某个原件（L或C），使其参数随调制电压变化，就可达到直接调频的目的。若被控制的是张弛振荡器，由于张弛振荡器的振荡频率取决与电路中的充电或放电速度，因此，可以用调制信号去控制电容的充电或放电电流，从而控制张弛振荡器的重复频率。对张弛振荡器调频，产生的是非正弦波调频信号，如三角波调频信号、方波调频信号等。

有各种不同的方法使LC振荡回路的电容或电感随输入信号而变化，如驻极体话筒或电容式话筒。常用的方法是采用变容二极管，还可以采用电抗管（在变容二极管问世前应用很广泛，现在很少使用）等。用变容二极管实现直接调频，由于电路简单、性能良好，已成为目前最广泛才用的调频电路之一。

在直接法调频中，振荡器与调制器合二为一。这种方法的主要优点是在实现线性调频的要求下，可以获得较大的频偏，其主要缺点是频率稳定度差，在许多场合需对载频采取稳频措施或者对晶体振荡器进行直接调频。

2. 间接调频法

这种方法是先将调制信号积分，然后对载波进行调相。这种方法也称为阿姆斯特朗（Armstrong）法。

间接调频的调制器与振荡器分开，对振荡器影响小，可以用高稳定的振荡器，产生的调频波其频率稳定度高。但一般为了作到线性调相，最大相偏较小，因而产生的调频波的最大频偏不能做得很大。为了得到大的频偏，通过倍频的方法可以将频偏扩大。因此，间接调频的设备一般比较复杂。

按照上述分类方法，本文所要实现的三角波调频电路调频器与振荡器合二为一，属于直接调频。

1.3调频三角波的应用

1. 调频三角波－调频正弦波

可通过调频三角波获得调频的正弦波。

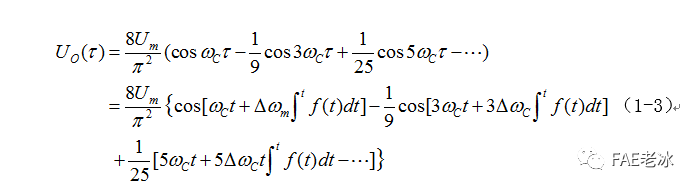
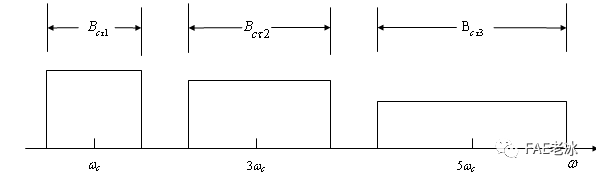
图1.1 调频三角波各谐波分量的带宽示意图

2. 三角波调频信号作为基本的调频信号，仍可以用于各种通信系统中，如调频广播等。
3. 调频三角波作为线性调频的连续波，在线性调频连续波雷达技术得到越来越多的关注。

第二章 三角波调频电路的设计

由于张弛振荡器的振荡频率取决于电路中RC的充电或放电速度，因此，可以用调制信号去控制电容的充电或放电电流，从而控制张弛振荡器的重复频率。对张弛振荡器调频，即可获得三角波调频信号、方波调频信号。

本章讨论了三种不同的实现三角波调频的电路方案，发射极耦合多谐振荡器构成的VCO实现三角波调频，积分－施密特触发电路实现三角波调频以及张弛振荡器直接调频电路实现三角波调频，并对最后一种做了详细说明并设计出具体电路。

2.1三角波调频电路实现方案

2.1.1发射极耦合多谐振荡器构成的VCO实现三角波调频

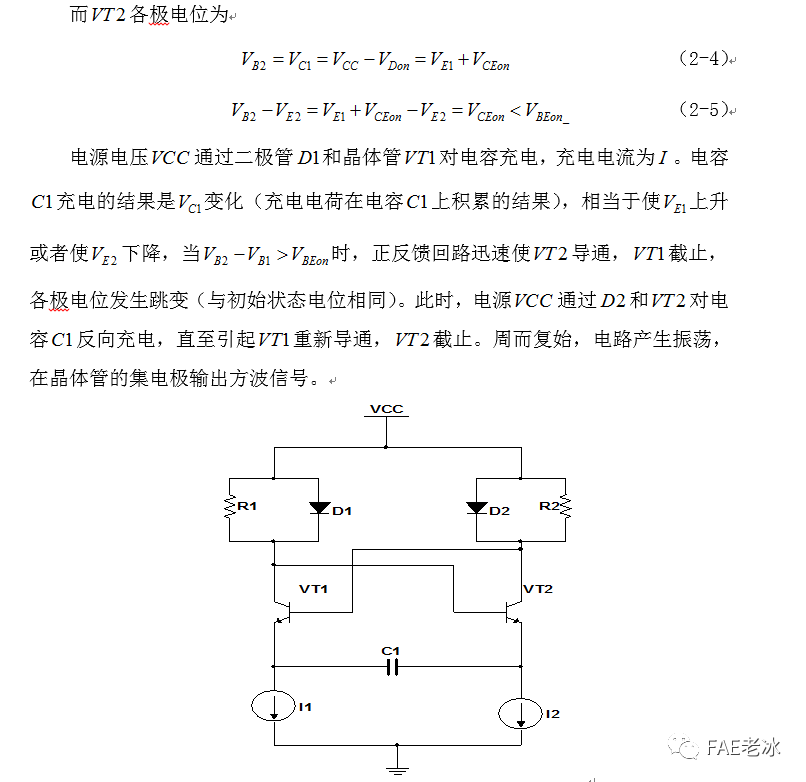
​图2.1发射极耦合多谐振荡器构成的VCO实现三角波调频原理图

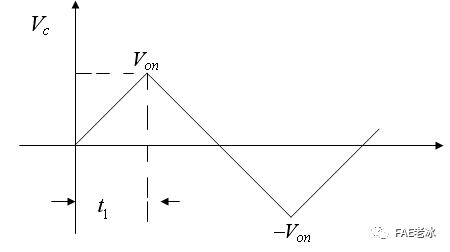
图 2.2电容器上电压变化

2.1.2 积分－施密特触发电路实现三角波调频

​

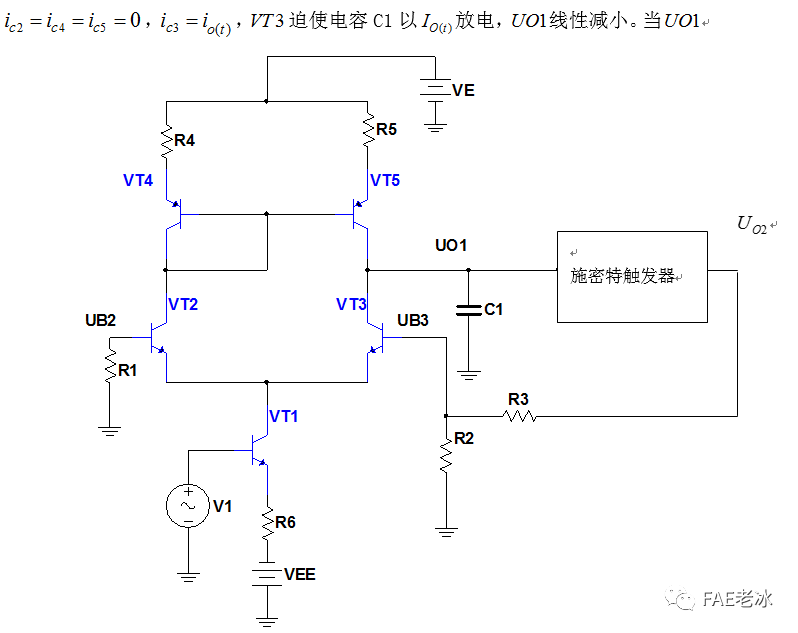
图2.3 积分－施密特触发电路实现三角波调频原理图

利用积分－施密特触发电路实现三角波调频，具有频偏大、调频线性好、电路便于集成等特点。

2.1.3张弛振荡器直接调频电路实现三角波调频

图2.4张弛振荡器直接调频电路实现三角波调频原理方框图

当外加调制电压时，输出三角波的频率与调制电压成线性关系，如此便可得到频率随调制电压变化的三角波。

2.2 方案对比及选择

方案一中 ：图2.1所示为集成压控振荡器MC1658的内部原理图，虽然原理简单，但由于还需较多的稳频和稳幅的外围电路才能使电路工作于一个较稳定的状态，且由独立元器件实现的电路调试困难，由于缺少经验，采用此方案实现三角波调频难度较大。

方案二中 ：且同方案一相似，需要稳频和稳幅的电路才能使电路稳定工作，调试，且调试困难，才用此方案难度较大。

方案三中: 极性转换器、积分器、比较器都可以用集成电路来实现，这样可以根据不同的需求选择不同的放大器来实现电路，且输出电路幅度可变且易于控制，这样的电路灵活、易于控制、便于调试。

因此，综合多方因素结合自身情况，我选择方案三中来实现三角波调频电路。

第三章 三角波调频电路的具体实现

本章根据所选方案设计出了具体的三角波调频电路，并按电路各个部分的主要功能将其分割成正负一倍放大器、反相积分器和迟滞比较器进行具体说明，使我们对电路的工作原理有清晰的认识，对电路的设计步骤和设计过程有了深刻体会。

3.1电路工作原理

实际电路如图3.1所示，主要由三部分组成，以运算放大器U1为核心的极性转换器，以运算放大器U2A为核心的反相积分器，以电压比较器U3A为核心的正相迟滞比较器。

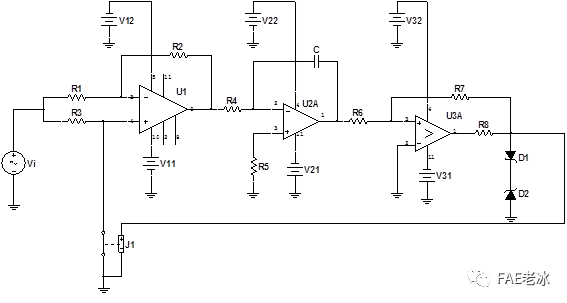
图3.1 三角波调频电路原理图

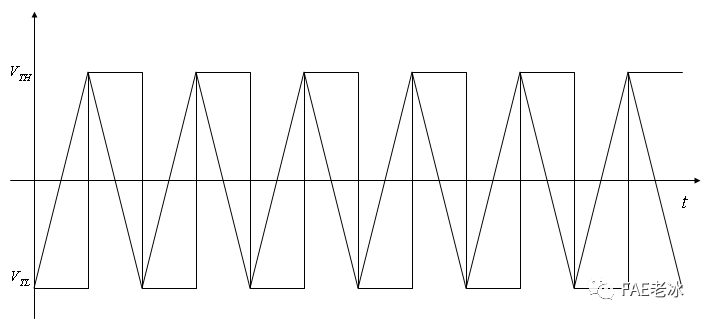
图3.2迟滞比较器输入输出波形

3.2具体电路的实现

整体的三角波调频电路如图3.1所示，电路主要由三部分组成，以U1为核心的极性转换器，以U2A为核心的反相积分器，以U3A为核心的正相迟滞比较器。下面就三个核心模块的实现及工作原理进行讨论。3.2.1 极性转换器的实现

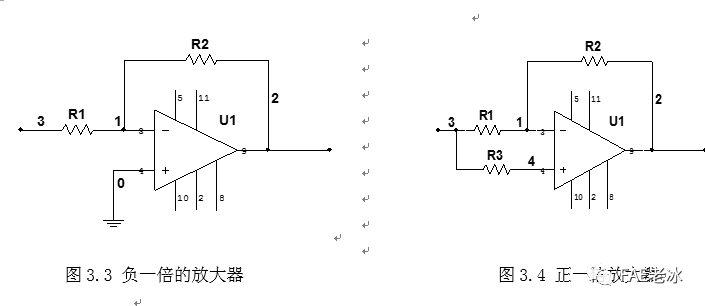
压控开关断开是时，压控开关等效电阻无穷小，放大器正相输入端相当于接地，此时该电路相当于负一倍的放大器，如图3.3所示。

压控开导通开时，压控开关等效电阻无穷大，运算放大器的同相输入端直接串联电阻R3，若运算放大器的输入电流为零（实际上为几纳安数量级的电流）,则此时的电路相当于正一倍的放大器，如图3.4所示。

极性转换器的实际电路如图3.5所示，开关是理想的压控开关，在实际电路中用压控开关通常用场效应管或者三极管来实现。

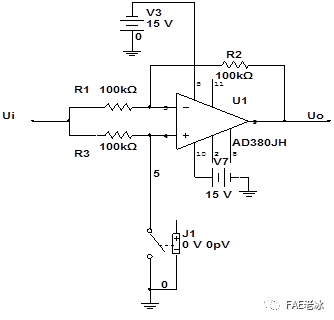
图3.5 极性转换器实际电路图

**3.2.2 积分器的实现 **

积分电路原理图如图3.6所示。

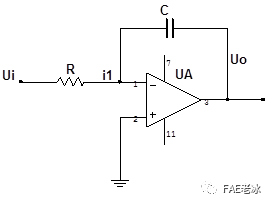
图3.6 积分器原理图

根据理想运算放大器线性区的两个重要依据：①理想运算放大器的两个输入端无电流，通常称为理想运算放大器的两个输入端之间开路；②线性工作时正相输入端和反相输入端时间差分电压为零，通常称为理想运算放大器的两个输入端“虚短路”。由于流入放大器的电流为零，所以流过电阻的电流和流过电容的电流相等，即i1=ic 。

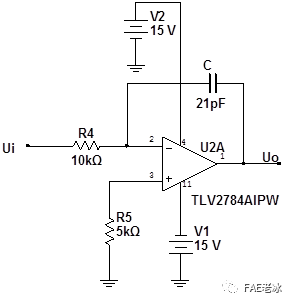
图3.7实际的积分器电路图

3.2.3 正相迟滞比较器实现

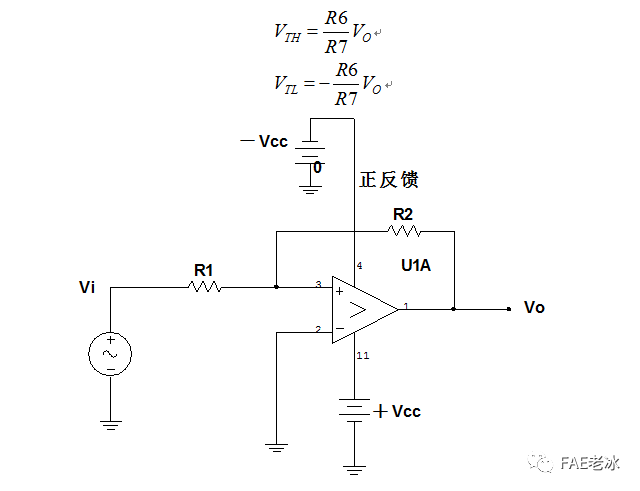
图3.8 正相迟滞比较器原理电路

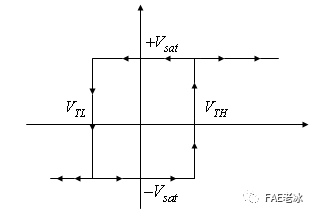​图3.9 正相迟滞比较器的转换特性曲线

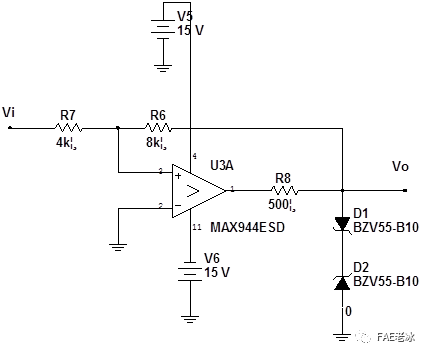
图3.10正相迟滞比较器电路

3.3本机元件选择及参数设置

整机电路如图3.1所示，极性转换器、积分器和迟滞比较器的实现电路及元件的参数见3.2节。电路中元器件的参数设置将在第四章中结合仿真进行说明。

第四章 电路模拟与测试

上一章我们设计了具体的实现三角波调频的电路，但未对元件参数设置做说明，在这一章中，我们在Multisim 10.0环境下对电路进行了模拟，根据理论并结合模拟的结果和经验讨论各个元件的选择和参数的设置问题，最后并测试电路在不同输入、不同状态下各点的输出波形和相关数据。

4.1电路的模拟及参数设置

极性转换器的参数设置

为了保证电路的工作频率和工作状态，必需选择转换速率SR和和电路工作频率相匹配的运算放大器，为了保证输出电压的与输入电压的误差较小，必需选择失调电压较小的放大器。

积分电路的参数设置

积分电路见图3.9，积分电路的输入输出关系见式（3-7），可见积电路的时常数RC越小则积分越快，对与本电路，三角波的斜率越大，即三角波的频率就越高。本电路中三角波频率的理论计算公式(式（3-3）)也证明了RC越大三角波频率越大，且RC越大调频电路的最大频偏也越大，但实际应用中太小的电容很难制造。

迟滞比较器的电路参数设置

总之，各个元件的参数设置并不能完全按照理论去设置，需要将理论和仿真结合来设置，因为理论计算时都是利用理想化的计算模型，与仿真模型有一定差距，与现实中的应用更有差距。当然理论值是电路模拟时参数设置的和应用于实际电路中元件选择重要参考，需要将理论和仿真结合来设置元件的参数，且由于电路存在反馈控制，整个电路输入与输出联系紧密，调整其中一个参数就有可能对其它部分的输入或输出产生影响，进而对其它原件的参数设置产生影响，因此，在选择元器件参数时更要综合整个电路来考虑，并且应结合仿真结果根据输入输出要求，在一定的误差范围内来选择原件的参数。

4.2载波信号测试

当输入调制信号为零，输入为一直流电压时，积分电路输出频率和幅度都稳定的三角波，即载波。

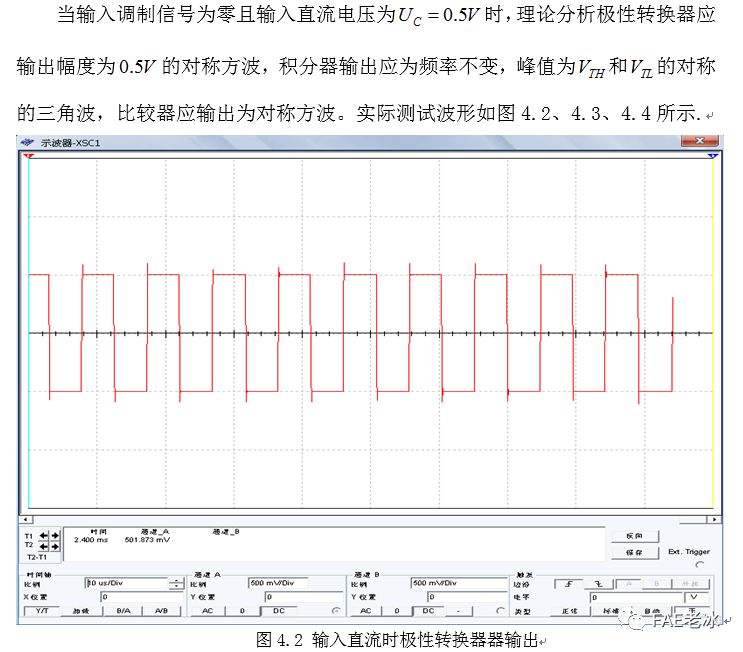
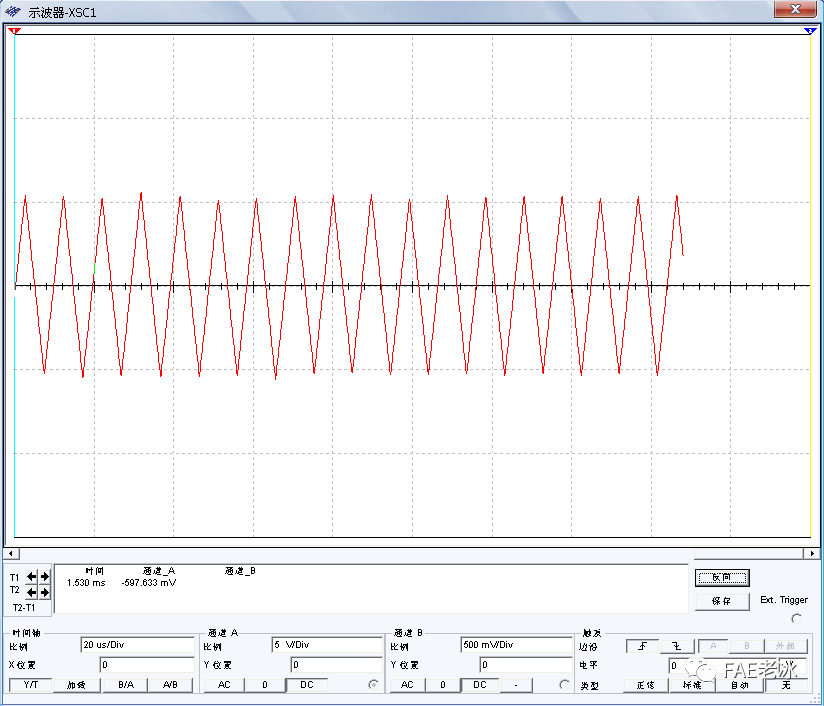
图4.3积分器输出的载波波形

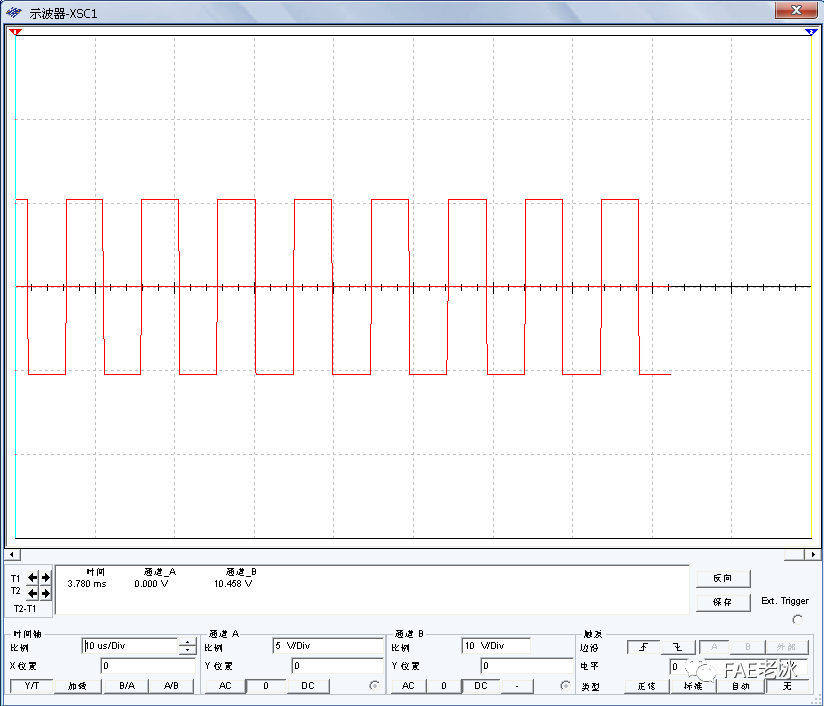
图4.4迟滞比较器经过稳压二极管稳压后的输出波形

当输入电压为一直流电压加三角波时，电路的输入与积分器输出波形对比图见图4.5.输入电压越大三角波波形越密，输入电压越小三角波波形越疏，这也证明了式（3-3），即三角波的频率和输入电压成正比。

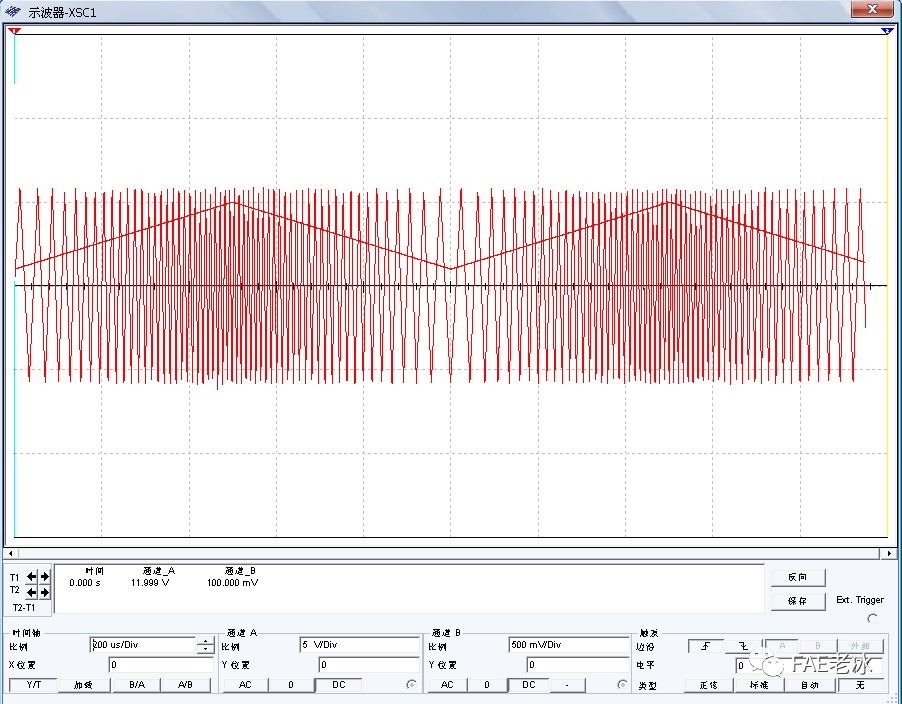
图4.5 输入直流电压加三角波时电路输入与积分器输出波形对比

4.3三角波调频信号测试

4.3.1电路工作于调频状态时各点波形测试

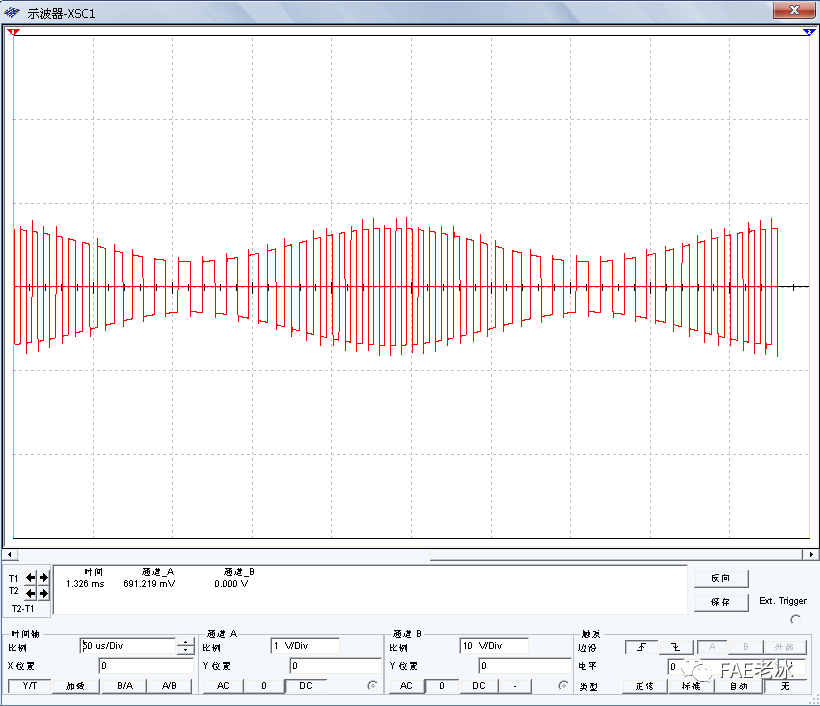
图4.6 调频时极性转换器输出波形

极性转换器输入与输出的对比如图4.7，可见极性转换器输出波形的包络与输入相同。

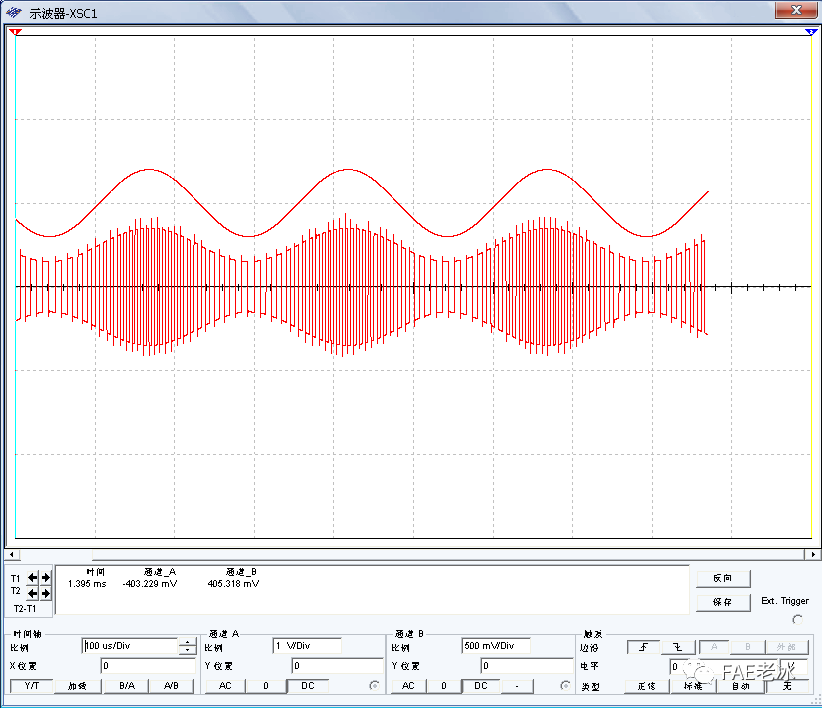
图4.7 极性转换器输入与输出的对比图

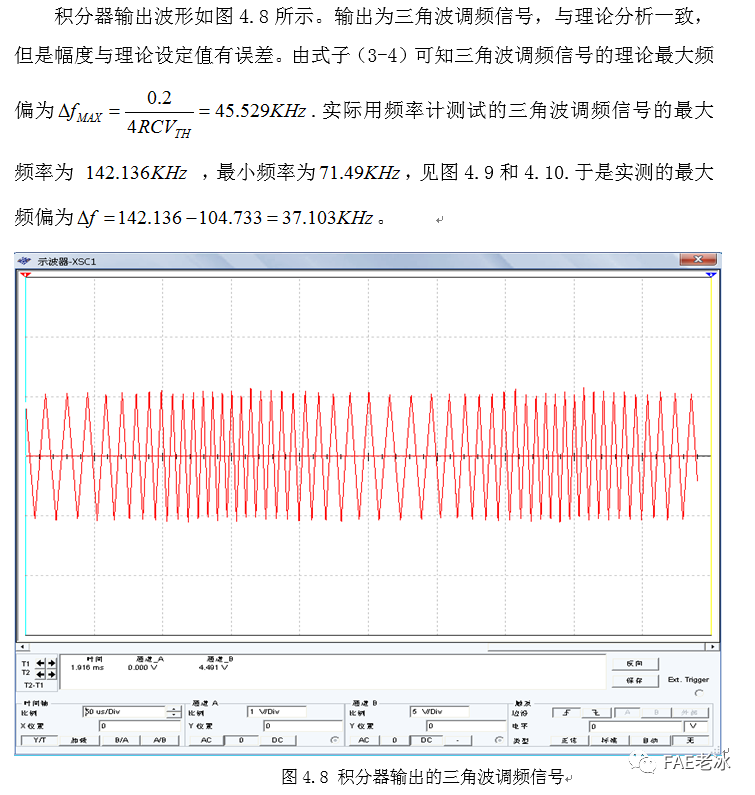
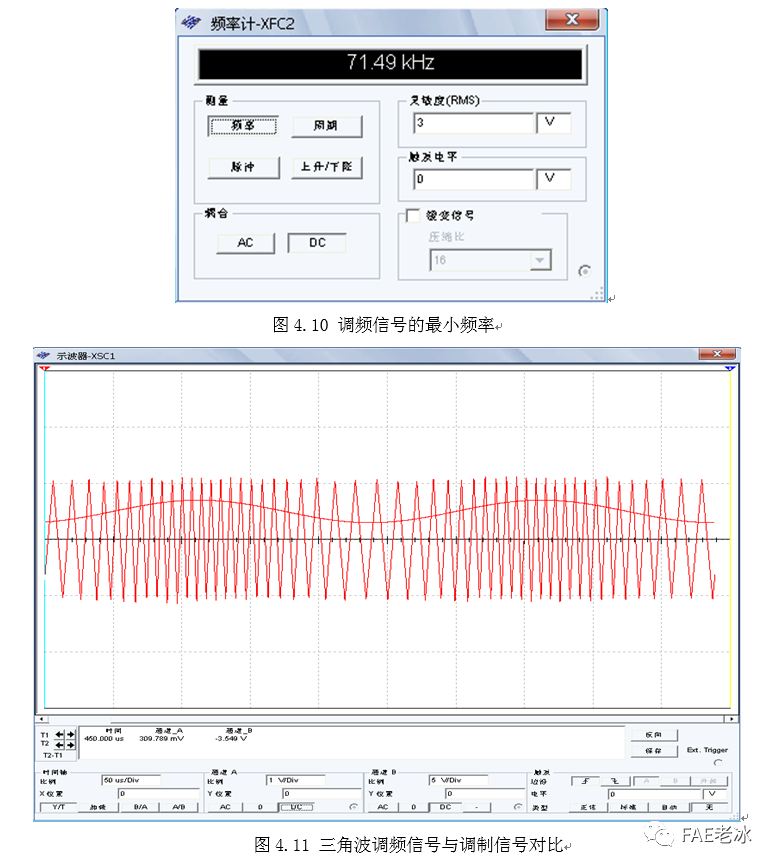
调制信号与三角波调频信号对比如图4.11所示，可见调制信号大的时候三角波频率大，波形密集，调制信号小的时候三角波频率小，波形稀疏。

比较器输出波形如图4.12所示，是调频的方波，与理论分析一致。

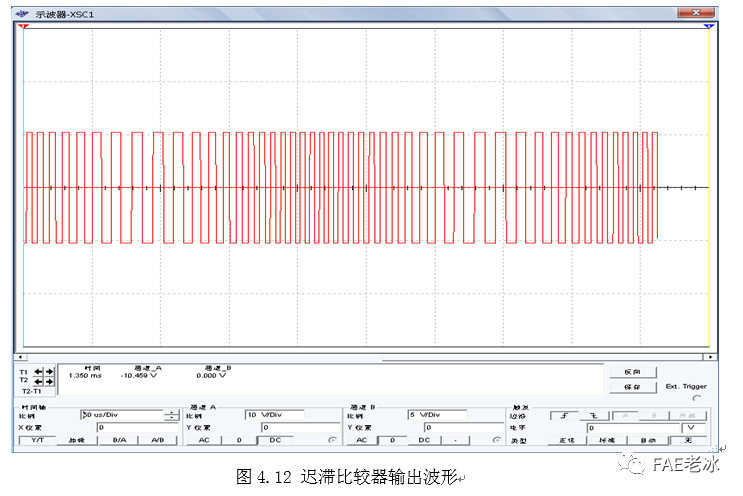
4.3.2 三角波调频信号参数测试

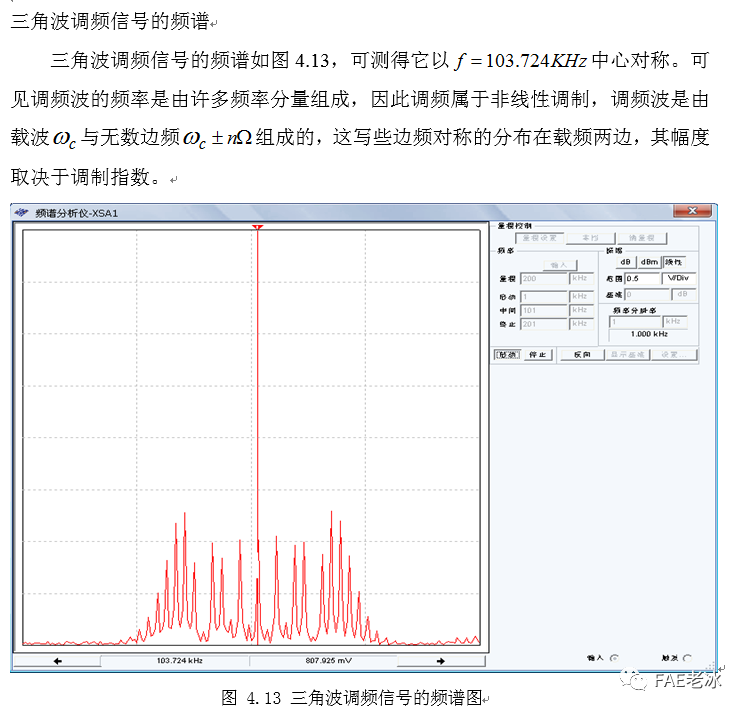
调频波的信号带宽

调频波的另外一个重要指标是信号的频带宽度。从原理上说，信号带宽应包括信号的所有频率分量。由于调频波有无穷多分量，这样定义的带宽显然是无意义的。从实际应用出发，调频信号的带宽是将大于一定幅度的频率分量包括在内，这样就可以是频带内集中了信号的决大部分功率，也不至因忽略其它分量而带来可察觉的失真。通常才用的准则是，信号的频带宽度应包括幅度大于未调载波1％以上的边频分量。

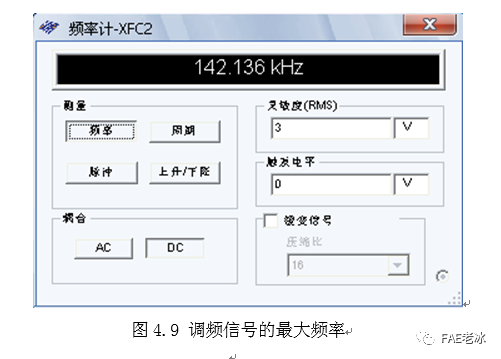
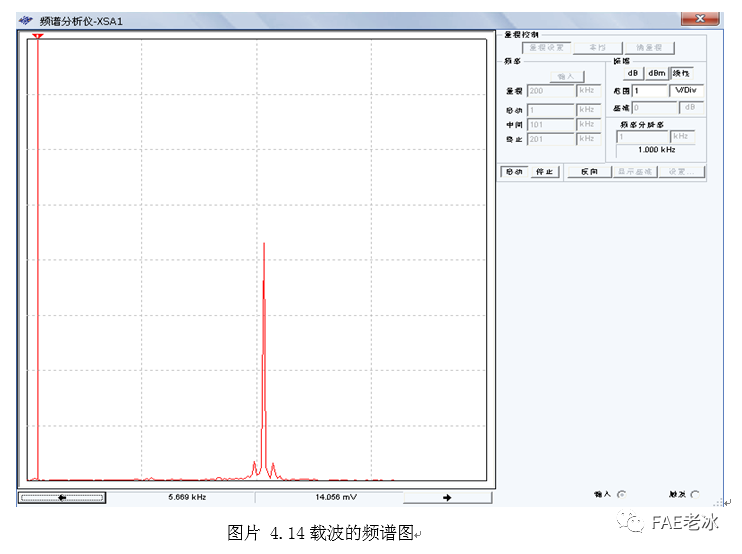
当输入调制信号为零，积分器输出的三角波（载波）频谱图如图4.14，且可测得当频率为104.113KHz时，幅度最大为3.846V。

按照上述准则，按照包括大于38.46mv的频率分量测试，可由三角波调频信号的频谱图中测得本当前三角波调频信号的信号带宽是。分布在之间。

4.4三角波调频电路的调频灵敏度测试

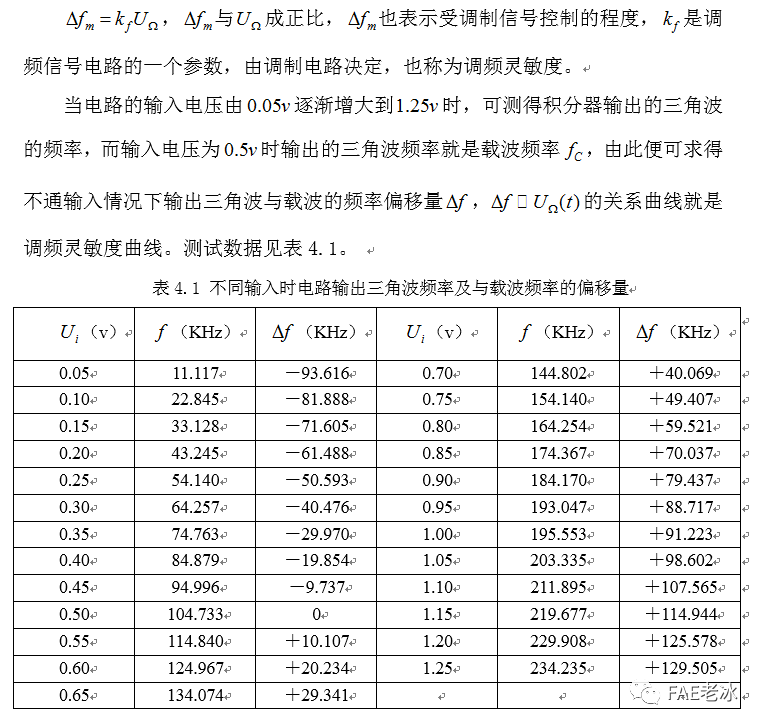
根据数据表4.1中的测试数据可绘的三角波调频电路的调制灵敏度曲线如图4.15，可见当输入的调制信号在一定范围内时调制信号与频偏是线性关系。