

信号完整性-容感性突变反射
电子说
描述
16.1
容性终端的反射
所有实际接收器都有门输入电容,一般约为2pF。此外,接收器的封装信号引脚与返回路径之间还会有约1pF的电容。这样,如果传输线末端排列着3个存储器件,则负载可能为10pF左右。
当信号沿传输线到达末端的理想电容器时,决定反射系数的瞬时阻抗将随时间的变化而变化。
如果信号上升边小于电容器的充电时间常数,那么最初电容器上的电压将迅速上升,这时阻抗很小。随着电容器充电,电容器上的电压变化率dV/dt缓慢下降,这时电容器阻抗将明显增大。如果时间足够长,电容器充电达到饱和,电容器就相当于断路。
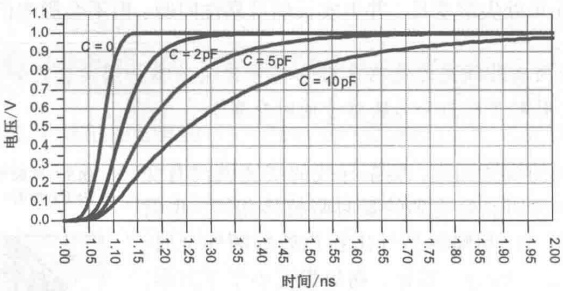
这意味着反射系数随时间的变化而变化。反射信号将先下跌再上升到开路状态时的情形。这个精确波形是由传输线特性阻抗Z_0、电容器的电容量和信号上升边决定的。下图给出了电容器容量分别为0pF、2pF、5pF和10pF时,仿真得到的反射信号和传输信号波形。
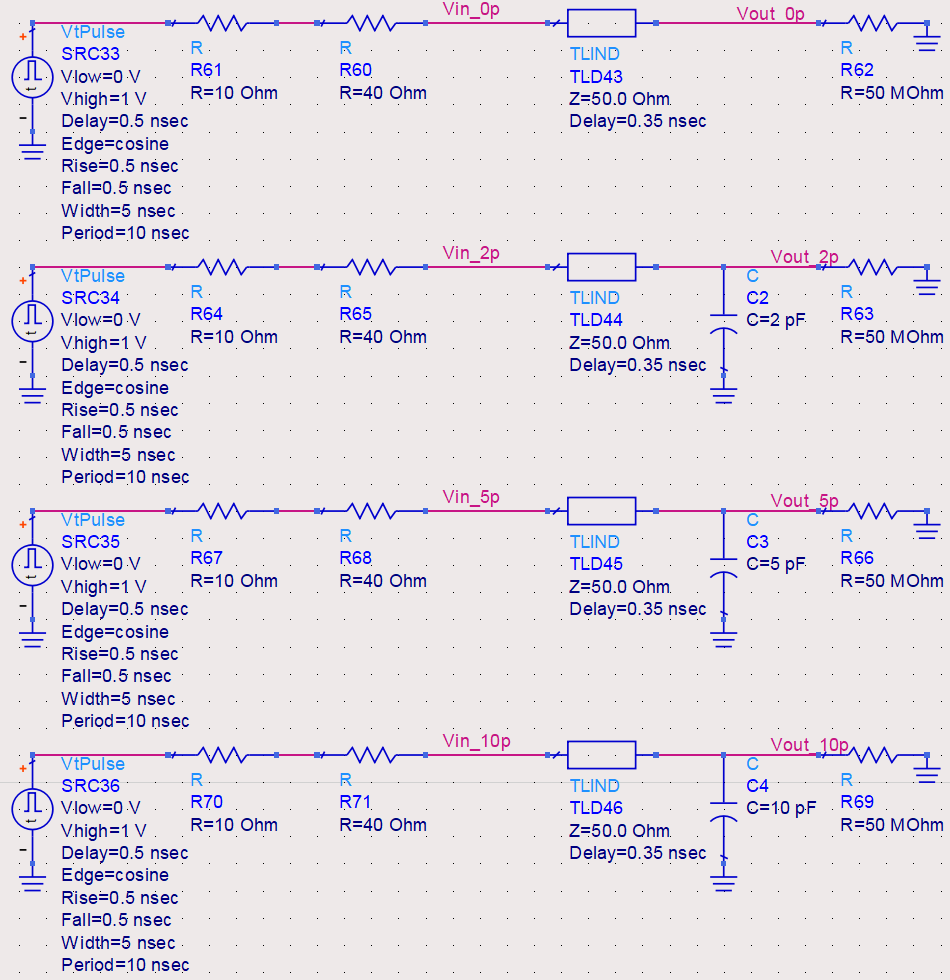
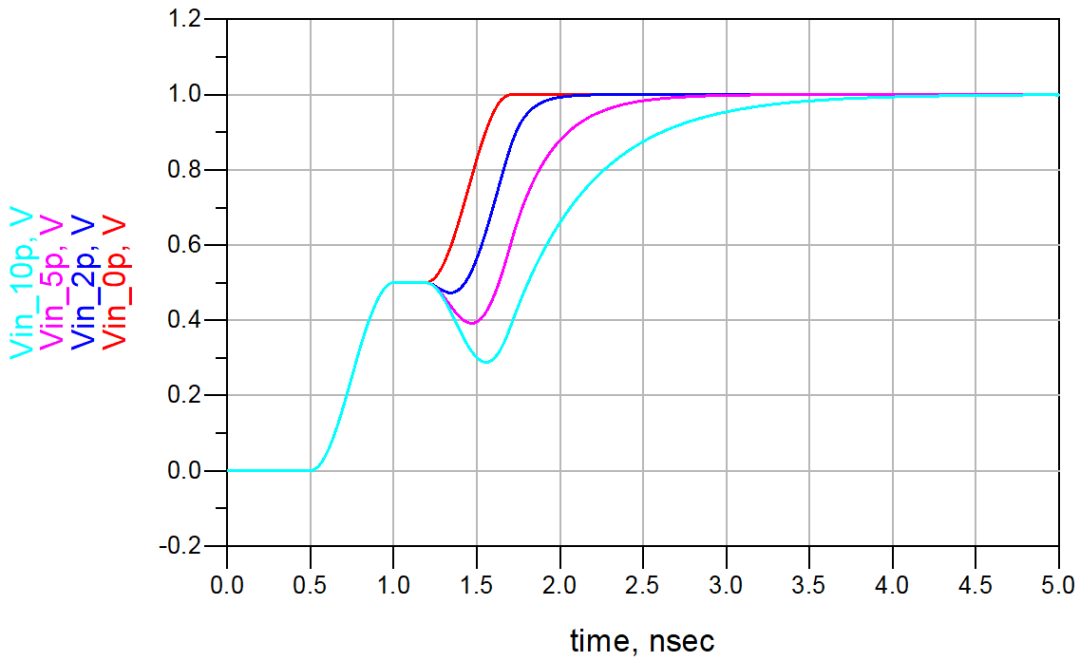
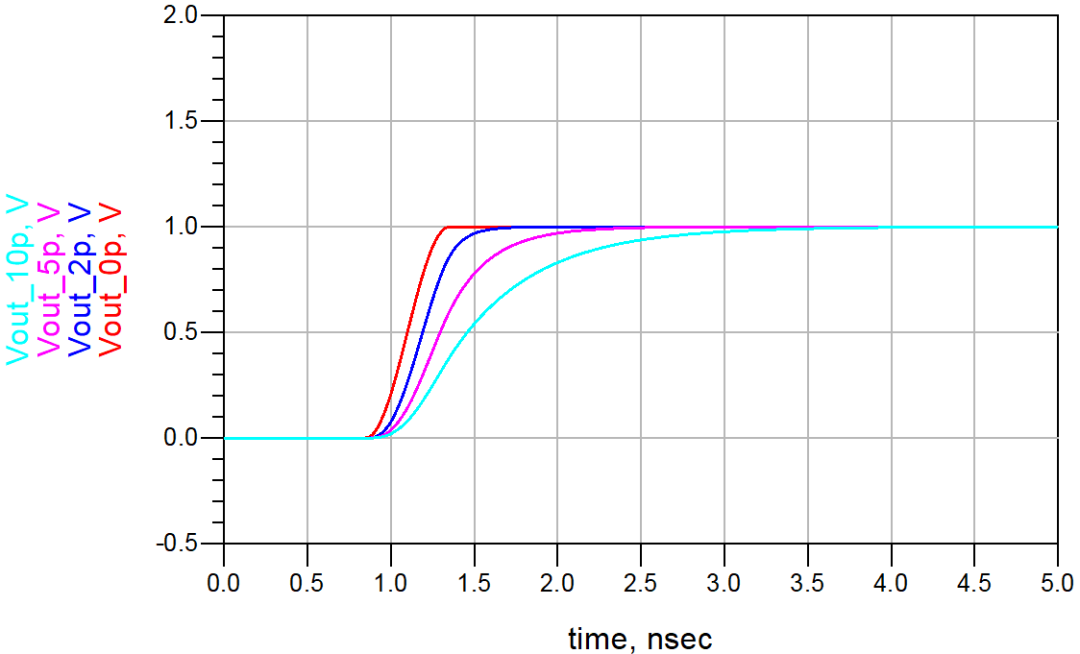
传输电压模式的长期效果就像通过电阻器向电容器充电。电容器对信号上升边进行滤波,对接收端信号而言,它就相当于一个“时延累加器”。它与RC电路的充电方式非常相似,电容器上的电压随时间呈指数增长。根据这一关系,可以估计出新的信号上升边升至幅度中间值的时延增加量,即时延累加。这里的时间常数为 τ_e=RC 。
这个时间常数是电压上升到电压终值的1/e或37%所需的时间。10%-90%上升边与RC时间常数的关系为 **τ_10%−90%=2.2τ_e=2.2RC** 。
在有容性负载的传输线末端,电压的变化形式就像RC在充电。其中C是负载的电容量,R是传输线特性阻抗Z_0。传输信号的10%-90%上升边主要由RC充电电路决定,约为 τ_10%−90%=2.2Z_0C 。
如果传输线的特性阻抗为50Ω,电容量为10pF,则10%-90%充电时间是 2.2×50×10=1.1ns 。如果信号的初始上升边比充电时间1.1ns短,则传输线末端的容性负载引起的时延将占主导地位,并决定接收端的上升边。如果信号的初始上升边大于10%-90%充电时间,那么末端的电容器将使信号上升边累加上约等于10%-90%RC上升边的时延。
电容量为2pF且特性阻抗为50Ω时,10%-90%RC上升边约为 2.2×50×2=0.2ns 。当初始上升边为1ns时,这个添加的0.2ns时延几乎无法辨认,显得不太重要。但当初始上升边为0.1ns时,0.2ns的RC时延就是一个重要的累加值了。当驱动远端的多个负载组合时,在所有时序分析中加入RC时延累加值就变得非常重要了。
16.2
走线中途容性负载的反射
测试焊盘、过孔、封装引线或连接到互连中途的短桩线,都起着集总电容器的作用。下图给出了线条上接入电容器时的反射电压和传输电压。起初,电容器形成的阻抗很低,反射到源端的信号幅度有轻微下降。所以,如果在靠近线条的前端处有接收器,这种下滑使信号边沿变成非单调的,就可能会产生问题。
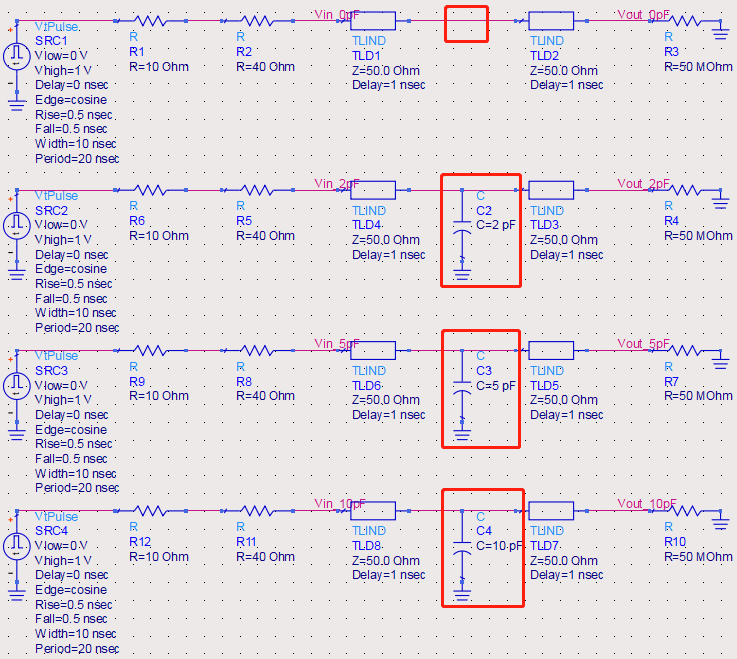
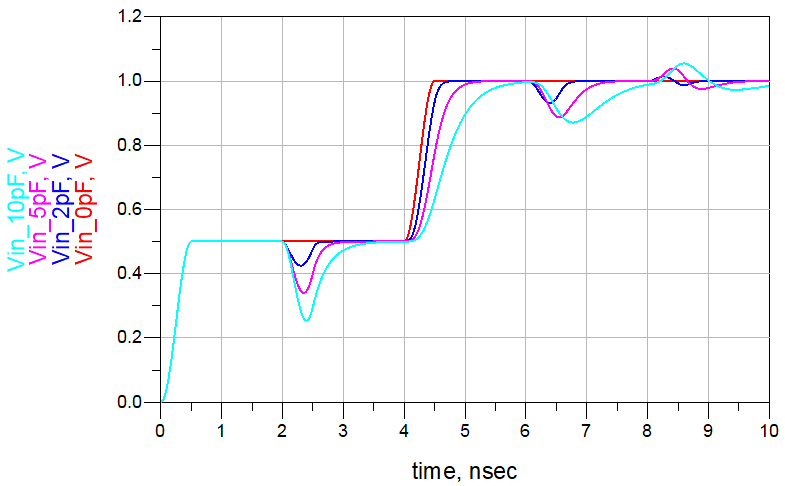
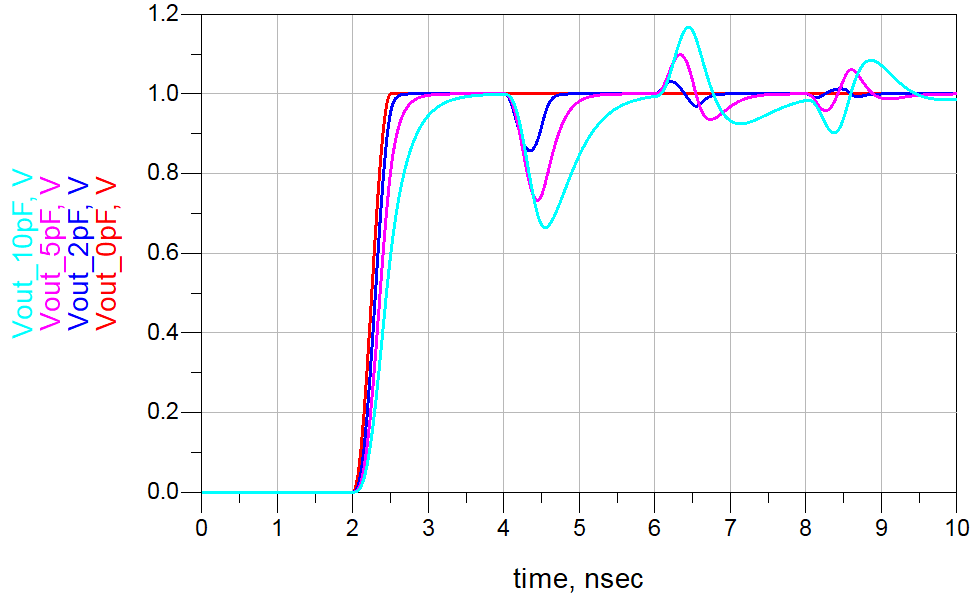
对于远端而言,第一次经过电容器的传输信号并没有受到太大影响。但当信号在末端发生反射后,它将向源端方向返回。当它再次到达电容器时,带负值符号的部分信号将反射回远端。这些反射回接收端的信号为负电压,使接收端信号下降形成下冲。
传输线中的理想电容器的影响由信号上升边和电容量决定。电容量越大,电容器阻抗就越小,负反射电压就越大,从而接收端的下冲也就越大。同理,上升边越短促,电容器阻抗就越小,下冲也就越大。
上升边与电容量比值的单位是Ω,它就是时域中电容器的阻抗,即:
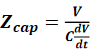
若信号是线性上升边,而且其上升边是RT,则dV/dt等于V/RT,所以电容器阻抗为:
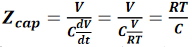
其中,Z_cap表示电容器阻抗(单位为Ω),C表示突变处的电容量(单位为nF),RT表示信号上升边(单位为ns)。
在信号上升过程中,信号路径与返回路径之间的电容器就是一个并联阻抗Z_cap。这个跨接在传输线上的并联阻抗引起了反射,如下图所示。为了避免该阻抗造成严重的问题,希望该阻抗能大于传输线的阻抗。可以简单地把这一条件理解为 Z_cap>5Z_0 。这样,对电容器和上升边的要求可以用下式表示: C_max 。其中,Z_cap表示信号上升过程中电容器的阻抗(单位为Ω),Z_0表示传输线的特性阻抗(单位为Ω),RT表示信号上升边(单位为ns),C_max表示反射噪声不出问题时可容许的最大电容量(单位为nF)。
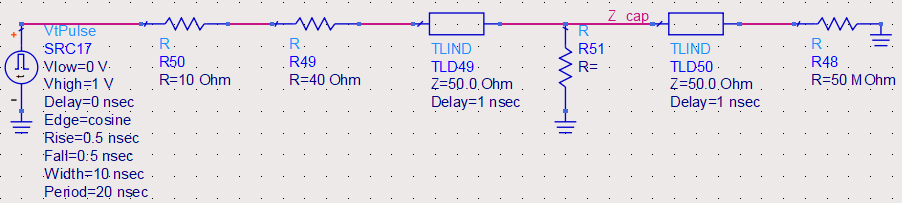
如果特性阻抗是50Ω,则所容许的最大电容量为: C_max 其中,RT表示信号上升边(单位为ns),C_max表示反射噪声不产生问题时可容许的最大电容量(单位为pF)。
经验法则 :为了避免容性突变造成过量的下冲噪声,应使电容量的pF值低于信号上升边ns值的4倍。
如果上升边是1ns,则最大可容许的电容量为4pF。如果上升边为0.25ns,则不会造成下冲问题的最大可容许电容量为 0.25×4=1pF 。同理,如果容性突变为2pF,那么不影响信号质量的最短上升边为 2/4=0.5ns 。
这一粗略的约束条件表明,如果系统上升边为1ns,则不会影响信号质量的容性突变约为4pF。同理,如果空连接器的电容量为2pF,上升边就需要大于0.5ns。这种情况下,如果上升边是0.2ns,就会产生问题。因此,在制作硬件前进行性能仿真是非常关键的。此时,需要寻找其他替代连接器或者更好的设计。
16.3
中途容性时延累加
****中途容性负载产生的第一位的影响就是接收端的下冲噪声。第二位的更复杂的影响则是远端信号的接收时间被延迟。电容器与传输线的组合就像一个RC滤波器,所以传输信号的10%~90%上升边将增加,信号越过电压阈值50%时间也将推后。传输信号的10%~90%上升边约为 **RT_10%~90%=2.2×RC=2.2×1/2Z_0C=Z_0C** ,50%的时延累加量称为 **时延累加** ,约为 **∆T** **_D=RC=1/2Z_0C** 。其中,RT_10%~90%表示信号上升边的10%~90%(单位为ns),∆T_D表示通过电压阈值50%时延累加(单位为ns),Z_0表示传输线的特性阻抗(单位为Ω),C表示容性突变(单位为nF),R为1/2Z_0。****
公式中的系数1/2是因为传输线的前一半使电容器充电,而后一半则使电容器放电,所以给电容器充电的有效阻抗实际上是特性阻抗的1/2。
例如,50Ω传输线中途的2pF容性突变,使传输信号的10%~90%上升边约增加 50×2=100ps 。50%阈值的时延累加约为 0.5×50×2=50ps 。下图给出了对于3个不同的容性突变,仿真得到的上升边。从中也可以看出接收端信号到达50%阈值时的时延。如果按公式进行预估,则2pF、5pF和10pF电容器对应的时延累加分别应为50ps、125ps和250ps。这些预估值与实际的仿真值非常接近。
要保证由测试焊盘、连接器焊盘和过孔引起的容性突变低于1pF是很困难的。每1pF焊盘约增加0.5×50×1=25ps的时延,从而延长了信号上升边。在高速链路中,如OC-48数据率甚至更高的情况,其上升边约为50ps。每个过孔焊盘或连接器都可能增加25ps时延,因此信号上升边的时延累加量可能为50ps。所以,一个过孔很容易使上升边翻倍而造成严重的时序问题。
使用低特性阻抗是减小时延累加影响的一种方法。对于同样的容性突变,特性阻抗越低,时延累加就越小。
16.4
拐角和过孔的影响
当信号沿均匀互连传播时,不会产生反射和传输信号的失真。如果均匀互连上有一个90°弯曲,则此处的阻抗发生改变,信号将出现部分反射和失真。任何均匀互连中的90°拐角一定会造成阻抗突变,影响信号质量。
将90°拐角变成两个45°拐角,就能减少这种影响,而使用线宽固定的弧形拐角比其他任何形状的效果好得多。
可能会认为90°拐角会使电子在其周围加速,从而导致过量的辐射和失真。如前所述,导线中的电子实际上是以约为1cm/s的速度缓慢移动的,拐角一点也不会影响电子速度。拐角尖端处的电场很高也是事实,但这是直流效应,它是由导线外边缘的尖锐程度引起的。很高的直流电场会使拐角处尖端变长,并引发长期可靠性问题,但不会影响信号质量。
弯曲处的额外线宽是使拐角影响信号传输的唯一因素,它如同一个容性突变。正是这个容性突变引起了反射和传输信号的时延累加。
如果拐角处导线的线宽固定,整条导线的线宽就没有变化,信号在拐角中的任何点处受到的瞬时阻抗将相同,也就不会产生反射。
拐角处的电容量大约估计为:
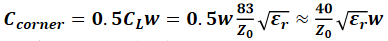
其中,C_corner表示每个拐角的电容量(单位为pF),C_L表示单位长度电容(单位为pF/in),w表示导线的线宽(单位为in),Z_0表示导线的特性阻抗(单位为Ω),ε_r表示介电常数。
例如,对于前面测量的65mil宽的导线,两个90°弯曲中的每个电容量约为 40/50×2×0.065=0.1pF 。因为邻近有两个拐角,总的突变容量则为0.2pF。
这种对拐角电容的估计可以简化为一个简单易记的 经验法则 :50Ω传输线上一个拐角的电容量(单位为fF)约等于两倍线宽(单位为mil)。
在保持阻抗仍为50Ω的同时减小线宽,拐角的电容量将下降,其作用会变得不那么明显。对于高密度电路板中线宽为5mil的典型信号线,一个拐角的电容量约为10fF。10F电容器产生的反射噪声如果对信号上升边有影响,上升边的数量级就必须在0.01/4≈3ps左右。而经过计算,此电容引起的时延累加约为 0.5×50×0.01=0.25ps 。所以,5mil宽的导线上拐角的电容量不太可能对信号完整性有很大的影响。
如果过孔把信号线连接到测试焊盘,或者过孔把信号线连接到相邻层上但又穿越所有板层,则筒状孔壁与板中不同平面层之间通常会有额外的电容量。残余的过孔桩线使过孔就像信号的一个集总容性负载。过孔桩线的电容量与筒状孔壁的尺寸、出砂孔及顶层和底层上焊盘的尺寸、桩线的长度等有密切的关系,其范围从0.1pF到1pF左右。任何与信号线相连的过孔都可以看成容性突变。在高速串接中,它是互连线信号质量的一个主要制约因素。
过孔的残余电容可以通过如下简单的近似关系得到。除非经特别小心处置,一般过孔处的有效特性阻抗,包括经过不同平面的返回路径,小于50Ω,约为35Ω。50Ω传输线的单位长度电容为3.3pF/in,那么过孔桩线的单位长度电容为5pF/in。即约为5fF/mil。根据这一经验法则可以估算出过孔桩线的容性负载。
例如,长度为20mil的过孔桩线,它的电容量为 20mil×5fF/mil=100fF 。位于较厚电路板上长度为100mil的过孔桩线,它的电容量为 100mil×5fF/mil=500fF ,也就是0.5pF。
下图给出了一块10层板中15in长的均匀传输线上分别有和没有通孔时,测得的时域反射响应,其中导线的阻抗约为58Ω,线宽为8mil,信号上升边约为50ps。导线中,SMA连接器的过孔和线中间位置上的通孔的电容量均约为0.4pF。致使这两个过孔产生的反射电压不同的原因是:当信号传播到中间位置及后续返回的过程中,介质损耗使信号上升边均发生了退化。沿线反射电压的其他起伏反映的是由于制造工艺波动引起的阻抗波动。
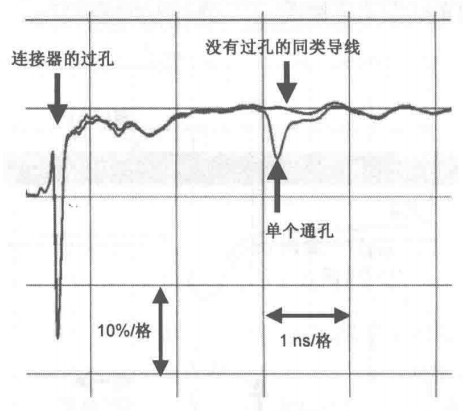
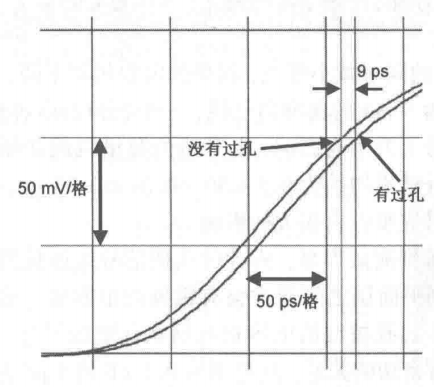
这个过孔的电容量近似为0.4pF,可预估这单个过孔产生的时延累加约为 0.5×50×0.4pF=10ps 。上图说明这个传输信号的时延比相同导线上没有过孔时增加了9ps。
16.5
有载线
当传输线上存在一个小的容性负载时,信号将失真,而且信号上升边也会退化。每个分立电容会降低它附近的阻抗。如果在导线上分布多个容性负载(如连接器的总线排上每隔1.2in就有一个2pF连接器桩线,或存储器的总线排上每0.8in就分布一个3pF的封装和输入门电容),而且它们的间距小于上升边的空间延伸,每个容性突变处引起的反射就会相互抵消。此时,等于是将导线的特性阻抗降低了。其上均匀分布着容性负载的传输线称为 有载线 。
每个突变看起来像一个低阻抗区域。当上升边小于电容之间的时延时,对于信号而言,每个突变都是彼此独立的。当上升边大于电容之间的时延时,低阻抗区域相互交叠,从而使导线的平均阻抗下降。
下图给出了3个上升边互不相同时,有载线的反射信号。该例中,导线的标称阻抗是50Ω,每隔1in分布一个3pF电容器,共有5个这样的电容器;最后10in导线是没有负载的无载线。每个电容器固有的10%~90%上升边约为 2.2×0.5×50×3=150ps 。即使初始上升边为50ps,在通过第一个电容器后,上升边也增加到150ps,而且每通过一个电容器都会继续增加。
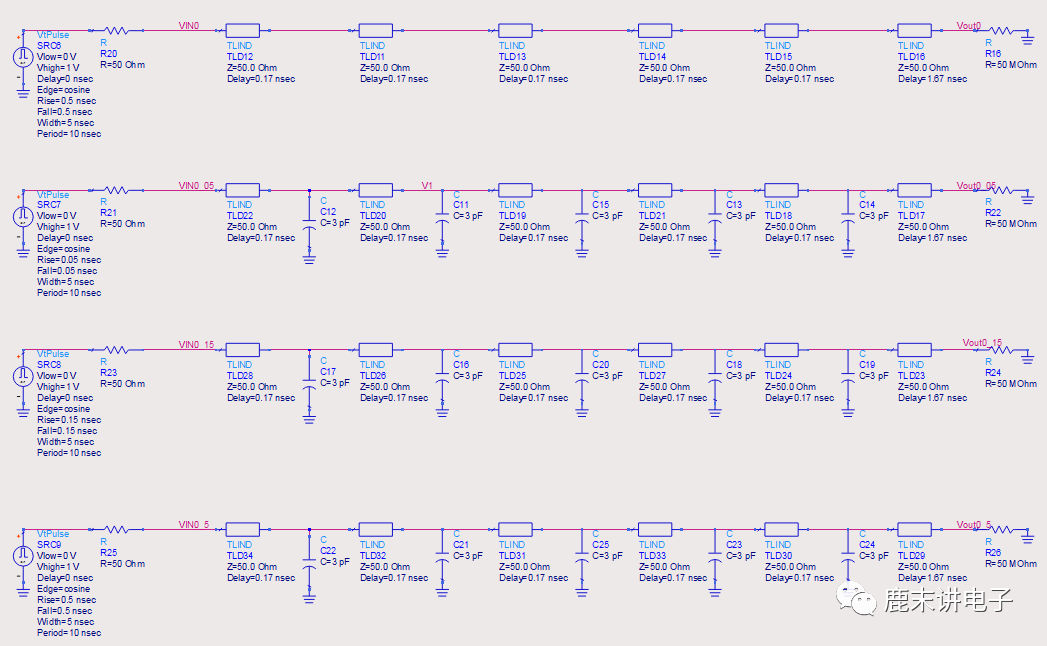
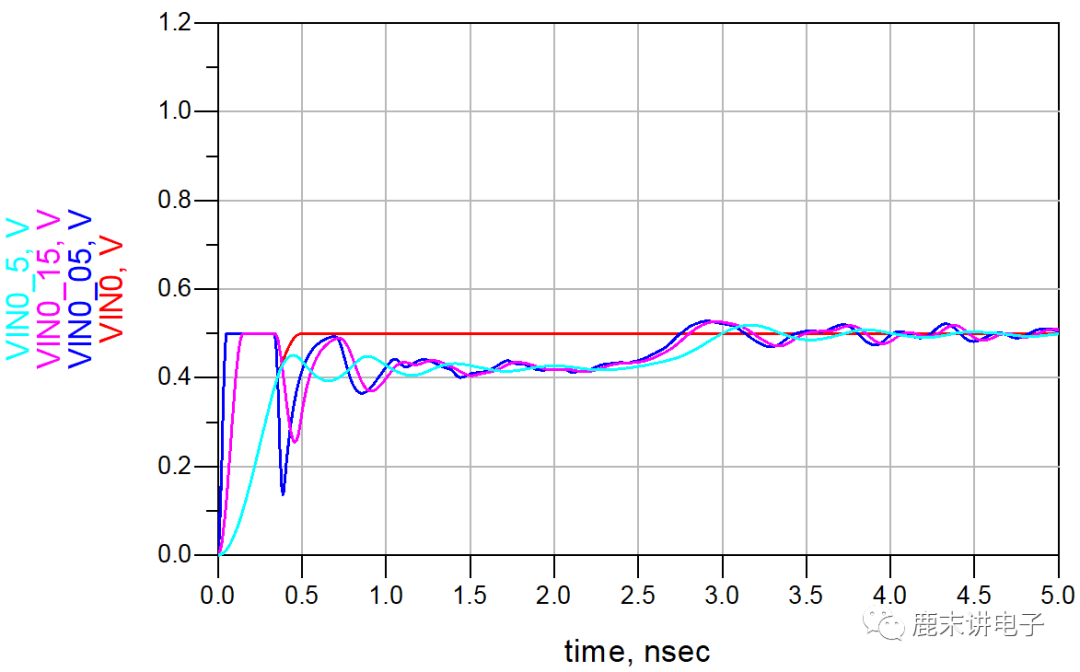
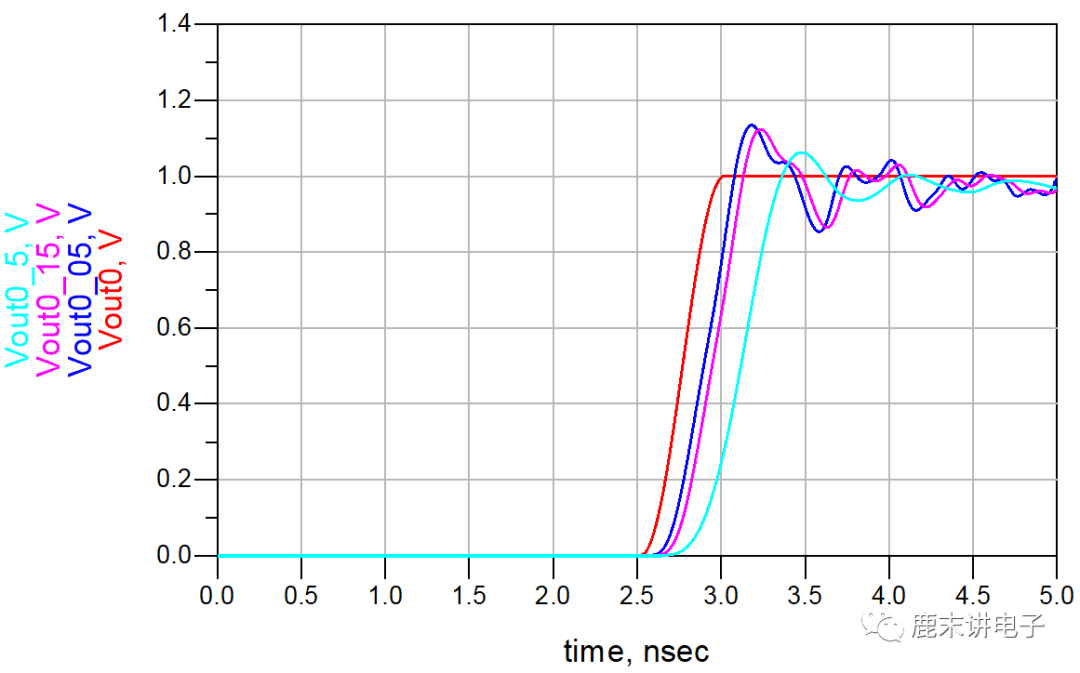
起初,电容器还可以看成独立的突变,但较长的信号上升边使后面电容器的作用相互抵消。当信号上升边大于容性突变之间的时延时,均匀分布的容性负载会降低导线的特性阻抗。在有载线上,电路板上这些额外的负载特征使导线的单位长度电容增加。单位长度电容越大,特性阻抗就越低,时延也就越长。
50Ω导线的单位长度电容约为3.4pF/in,当添加的分布式容性负载与此值相当时,特性阻抗和时延就有明显的改变。例如,一个多支路总线排上每隔1in有一个3pF的内存条输入门电容负载,则单位长度上添加的负载电容为3pF/in,负载特性阻抗降低到0.73Z_0,时延提升到1.37T_D0 。
随着导线特性阻抗的降低,用于端接匹配的电阻也应随之降低。或者,在有分布式电容的区域内,通过减小线宽,使无载阻抗变大。这样,最后的效果可以使有载线的阻抗比较接近于期望的阻抗值。分立电容的加大对导线的作用就是降低了特性阻抗并加大了时延,它与在过孔中所发生的情况相同。
在焊盘叠层的每一层上的任何非功能性焊盘,或者只是穿越平面出砂孔的过孔桶壁的额外电容,粗看就像增加了分立电容,从而导致了过孔的阻抗降低,基于过孔长度和叠层介质材料介电常数Dk的时延也会加大。
与大多数Dk为4不同,这里好像有一个高达8~15的有效Dk。这都是由于过孔桶壁与平面之间的离散负载电容较高所造成的。
16.6
感性突变的反射
连接到传输线上的任何串联连接都有一些相应的串联回路电感。改变信号所在层的所有过孔、串联端接电阻器、各种连接器及每个工程变更线,都有一些额外的回路电感,信号认为这些回路电感是在传输线上加入的突变。
如果信号路径上出现突变,则虽然信号路径与返回路径之间有局部互感,回路电感也主要由信号路径上突变引起的局部自感决定。如果返回路径上出现突变,返回路径上突变引起的局部自感就决定了回路电感。
对于边沿快速上升的入射信号,大的串联回路电感初看是一个高阻抗元件,所以产生返回源端的正反射。
下图为不同感性突变情况下的源端和接收端的信号。近端信号的形状为先上升后下降,称为非单调性,即信号不是稳定一致地单调上升。这一特征本身并不会造成信号完整性问题。然而,如果近端有接收器,并且它接收到的信号先是超过50%点,再下降到50%点以下,就有可能造成误触发。
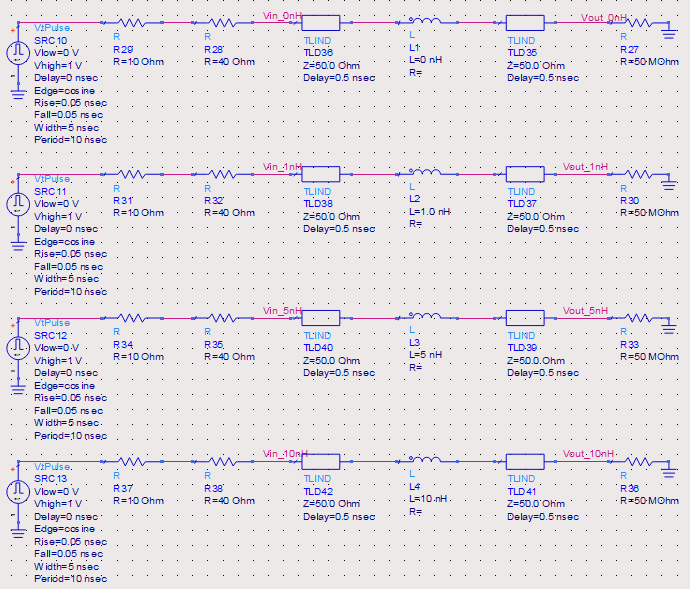
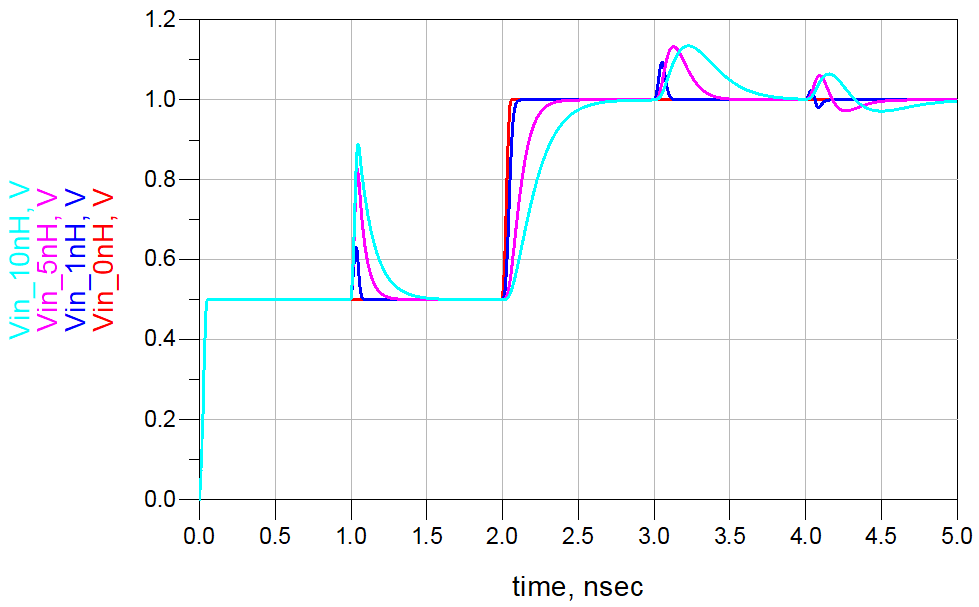
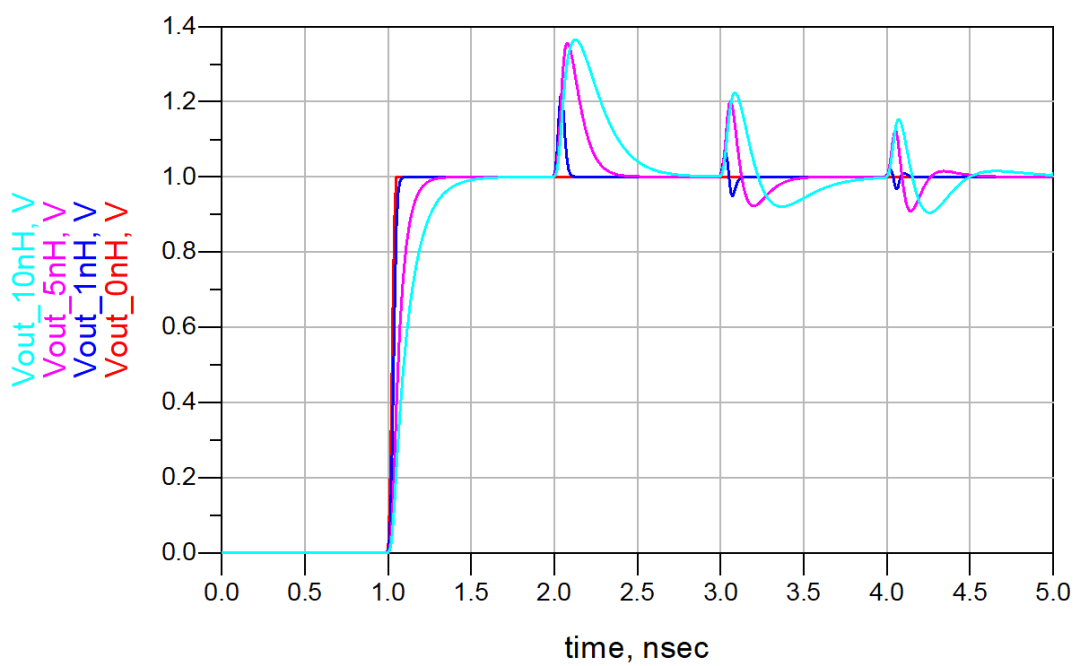
如果接收器中信号初始的上升边或下降边的边沿失真发生在规定的建立和保持时间,就可能不会造成误码。然而,时钟信号的边沿发生失真却会导致一个时序错误,从而造成一个误码。
这种信号非单调性在任何地方都应尽量避免。在远端,传输信号出现过冲,并有一个时延累加。
总之,电路中可容许的最大电感总量取决于噪声容限和电路的其他特征,通常每一种情况都必须通过仿真去估计是否可行。不过,也可以按分立电感器这一串联阻抗突变引起的增量小于导线特性阻抗的20%为限,粗略估算多大的电感就算太大。此时,反射信号约为信号摆幅的10%,对反射噪声而言,这通常就是可以容许的最大噪声了。
当信号的上升边通过电感器时,如果电感器的阻抗小于特性阻抗,而且信号的上升边是线性上升的,则电感器的阻抗约为:
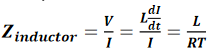
其中,Z_inductor表示电感器的阻抗(单位为Ω),L表示电感(单位为nH),RT表示信号的上升边(单位为ns)。
为了确保电感器的阻抗低于导线阻抗的20%,可容许的最大感性突变约为 L_max<0.2Z_0×RT 。其中,L_max表示可容许的最大串联电感(单位为nH),Z_0表示导线的特性阻抗(单位为Ω),RT表示信号的上升边(单位为ns)。
通过粗略的估算,50Ω导线上可容许的最大额外回路电感(单位为nH)为信号上升边(单位为ns)的10倍。同理,如果突变形成了回路电感,则为了使反射噪声不超过噪声预算,可容许的最短上升边(单位为ns)为电感(单位为nH)的1/10。
为了保证反射信号不造成问题,使用轴向引脚电阻器时,信号的最短上升边约为10nH/101ns。而对于SMT电阻器,信号的最短上升边约为2nH/100.2ns。
****感性突变会引起反射噪声和时延累加。若上升边很短,信号的上升边主要由串联电感决定,则传输信号的10%~90%上升边约为 **T_D10%~90%=2.2×L/2Z_0=L/Z_0** 。其中,T_D10%~90%表示传输信号的10%~90%上升边(单位为ns),L表示突变处的串联回路电感(单位为nH),Z_0表示导线的特性阻抗(单位为Ω)。****
16.7
补偿
设计中常常要用到专用连接器,电路中的串联回路电感是不可避免的。如果不加以控制,它就可能造成过量的反射噪声。补偿技术就是为了抵消部分此类噪声。
补偿的概念就是尽量让信号感受不到很大的感性突变,而是觉得遇到了与导线特性阻抗相匹配的一段传输线。既然理想传输线可以用单节LC网络实现一阶近似,在感性突变两侧各加一个小电容器,就能将感性突变转变成一节传输线,如下图所示:
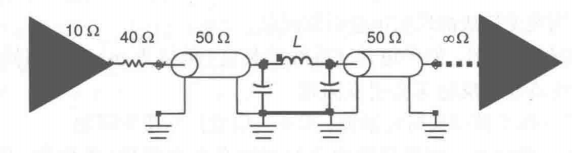
为了最小化反射噪声,就要找到合适的电容值,使连接器的实在特性阻抗Z_1等于电路其余部分的特性阻抗Z_0。基于这个关系式,添加的电容为 C_1=L_1/Z_0^2 ,其中,C_1表示添加的总补偿电容(单位为nF),L_1表示突变处的电感(单位为nH),Z_0表示导线的特性阻抗(单位为Ω)。
****例如,如果连接器的电感为10nH,导线的特性阻抗为50Ω,则所要加上的总补偿电容为 **10/(50×50)=0.004nF=4pF** 。最优的补偿方式是将4pF电容分为两部分,分别加在电感器的两侧,即各为2pF。****
下图给出了无连接器、无补偿连接器和有补偿连接器这3种情况下的反射和传输信号。根据系统的上升边,反射噪声有时能降低75%。
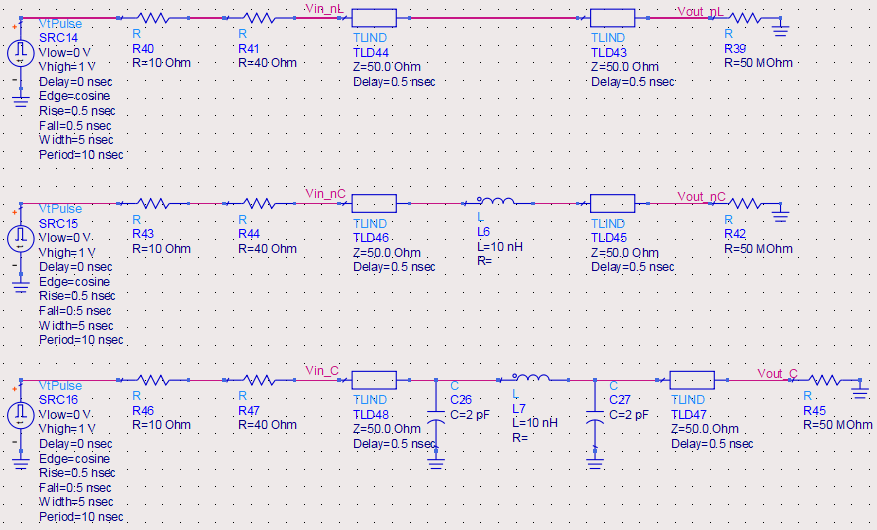
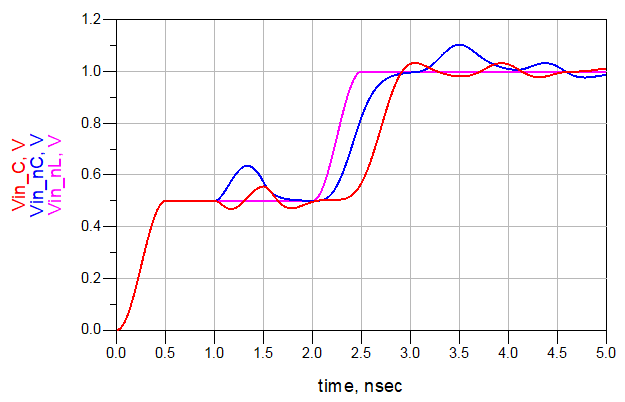
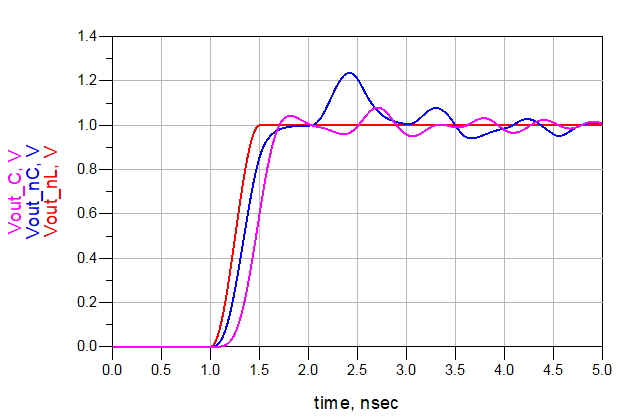
这一技术适用于所有的感性突变,如过孔、电阻器等。根据焊盘上的电容和电感总量,可以把实际突变看成容性的或感性的。
互连设计目标就是控制焊盘和其他特征,使它们的结构如同均匀传输线的一部分。用这种方法,一些感性突变(如连接器)的现象几乎可以消失。
-
[推荐]信号完整性仿真应用技术高级研修会2009-11-18 7047
-
2011信号及电源完整性分析与设计2010-12-16 3468
-
【连载笔记】信号完整性-基本含义2017-11-22 2625
-
PCB信号完整性2018-11-27 2649
-
信号完整性(五):信号反射2019-05-31 1861
-
何为信号完整性?信号完整性包含哪些2021-12-30 2763
-
信号完整性与电源完整性仿真分析2011-11-30 1989
-
信号完整性原理2016-08-29 1121
-
信号完整性简介及protel信号完整性设计指南2017-11-16 1343
-
信号完整性的“反射”的心路历程2021-04-13 3328
-
信号完整性与电源完整性的仿真2021-09-29 1499
-
信号完整性之反射(一)2023-04-15 2946
-
信号完整性分析科普2023-08-17 8595
-
信号完整性阻抗突变处为什么会有反射呢?2023-09-22 3131
-
串扰和反射影响信号的完整性2023-11-30 1118
全部0条评论

快来发表一下你的评论吧 !

