三维点云配准算法原理及推导

‍‍作者 | 刘缘

1点云配准过程 就是求一个两个点云之间的旋转平移矩阵（rigid transform or euclidean transform 刚性变换或欧式变换），将源点云(source cloud)变换到目标点云(target cloud)相同的坐标系下。 可以表示为以下的方程: 其中就是target cloud与source cloud中的一对对应点。 而我们要求的就是其中的R与T旋转平移矩阵。 这里，我们并不知道两个点集中点的对应关系。这也就是配准的核心问题。

2

配准分为粗配准与精配准两步

粗配准就是再两个点云还差得十万八千里、完全不清楚两个点云的相对位置关系的情况下，找到一个这两个点云近似的旋转平移矩阵（不一定很精确，但是已经大概是对的了）。 精配准就是在已知一个旋转平移的初值的情况下（这个初值大概已经是正确的了），进一步计算得到更加精确的旋转平移矩阵。 这里从精配准开始讲起。 精配准的模式基本上已经固定为使用ICP算法及其各种变种。ICP算法由Besl and McKay 1992, Method for registration of 3-D shapes文章提出。 文中提到的算法不仅仅考虑了点集与点集之间的配准，还有点集到模型、模型到模型的配准等。 简要介绍一下点集到点集ICP配准的算法：

1) ICP算法核心是最小化一个目标函数：

（这里的表述与原文略微有些不同，原文是用四元数加上一个偏移向量来表达旋转平移变换。）就是一对对应点，总共有对对应点。这个目标函数实际上就是所有对应点之间的欧式距离的平方和。

2) 寻找对应点 可是，我们现在并不知道有哪些对应点。因此，我们在有初值的情况下，假设用初始的旋转平移矩阵对source cloud进行变换，得到的一个变换后的点云。 然后将这个变换后的点云与target cloud进行比较，只要两个点云中存在距离小于一定阈值（这就是题主所说的ICP中的一个参数），我们就认为这两个点就是对应点。这也是"最邻近点"这个说法的来源。
3) R、T优化 有了对应点之后，我们就可以用对应点对旋转R与平移T进行估计。这里R和T中只有6个自由度，而我们的对应点数量是庞大的（存在多余观测值）。因此，我们可以采用最小二乘等方法求解最优的旋转平移矩阵。一个数值优化问题，这里就不详细讲了。

4) 迭代 我们优化得到了一个新的R与T，导致了一些点转换后的位置发生变化，一些最邻近点对也相应的发生了变化。 因此，我们又回到了步骤2)中的寻找最邻近点方法。2)3)步骤不停迭代进行，直到满足一些迭代终止条件，如R、T的变化量小于一定值，或者上述目标函数的变化小于一定值，或者邻近点对不再变化等。（这里也是题主所说的ICP算法中的一个参数） 算法大致流程就是上面这样。这里的优化过程是一个贪心的策略。首先固定R跟T利用最邻近算法找到最优的点对，然后固定最优的点对来优化R和T，依次反复迭代进行。 这两个步骤都使得目标函数值下降，所以ICP算法总是收敛的，这也就是原文中收敛性的证明过程。这种优化思想与K均值聚类的优化思想非常相似，固定类中心优化每个点的类别，固定每个点的类别优化类中心。 关于参数的选择: ICP算法的参数主要有两个。一个是ICP的邻近距离，另外一个是迭代的终止条件。这些参数的选择，与实际的工程应用相关。比如说你的仪器精度是5mm，那么小于5mm是可以认为是对应点，而最终的迭代终止条件也就是匹配点之间平均距离小于5mm。 而且这些参数可以由算法逐步迭代减小，最初使用较大的对应点距离参数，然后逐步减小到一个较小的值。（问过师兄才知道实际过程这样操作会比较合适。）需要手动调整一些参数。（这跟机器学习调参比起来，简直不是事~）

3

粗配准

前面介绍到了，ICP算法的基本原理。它需要一个旋转平移矩阵的初值。这个初值如果不太正确，那么由于它的greedy优化的策略，会使其目标函数下降到某一个局部最优点（当然也是一个错误的旋转平移矩阵）。因此，我们需要找到一个比较准确的初值，这也就是粗配准需要做的。 粗配准目前来说还是一个难点。针对于不同的数据，有许多不同的方法被提出。

我们先介绍配准的评价标准，再在这个标准下提出一些搜索策略。 评价标准：比较通用的一个是LCP(Largetst Common Pointset)。给定两个点集P,Q，找到一个变换T(P)，使得变换后的P与Q的重叠度最大。在变换后的P内任意一点，如果在容差范围内有另外一个Q的点，则认为该点是重合点。重合点占所有点数量的比例就是重叠度。 解决上述LCP问题，最简单粗暴的方法就是遍历。假设点集P,Q的大小分别为m,n。而找到一个刚体变换需要3对对应点。 那么brute force 搜索的需要的复杂度。对于动辄几百万个点的点云，这种时间复杂度是不可接受的。 因此，许多搜索策略被提出。比较容易想到的是RANSAC之类的搜索方法。而对于不同的场景特点，可以利用需配准点云的特定信息加快搜索。（例如知道点云是由特定形状的面构成的）这里先介绍一个适用于各种点云，不需要先验信息的搜索策略，称为4PC(4 Point Congruent)。 搜索策略：4PC搜索策略是在P,Q中找到四个共面的对应点。

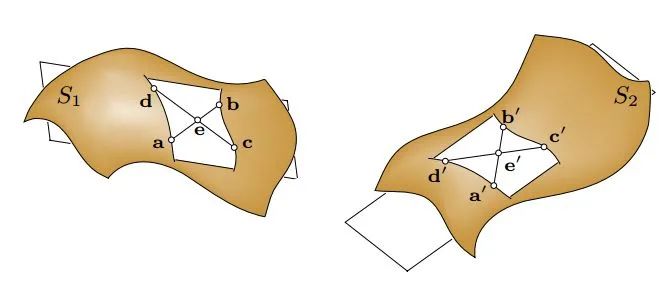
如上图所示（来自4PC原文），这四个共面的点相交于e。这里有两个比例在刚体变化下是不变的。(实际上在仿射变换下也是不变的) 而4PC将对于三个点的搜索转换为对e,e'的搜索，从而将复杂度降低到了。 这四个点的距离越远，计算得到的转换越稳健。但是这里的四个点的搜索依赖于两个点云的重叠度。 具体的算法可以参考4-Points Congruent Sets for Robust Pairwise Surface Registration的原文。 4PC算法通用性较好，但是对于重叠度较小、或是噪声较大的数据也会出现配准错误或是运行时间过长的问题。针对于不同的场景很多其他的搜索策略也被提出。 这里安利一下我师兄的论文吧~Automatic registration of large-scale urban scene point clouds based on semantic feature points 我们课题组主要是研究室外地面站LiDAR获取的点云配准问题。这种情形下，由于扫描仪内有自动安平装置，Z轴都是竖直方向（重力方向），刚体变换只存在三维平移与平面（XoY面上的）旋转。我们就在场景中搜索竖直的特征线并且得到它们与地面的交点。

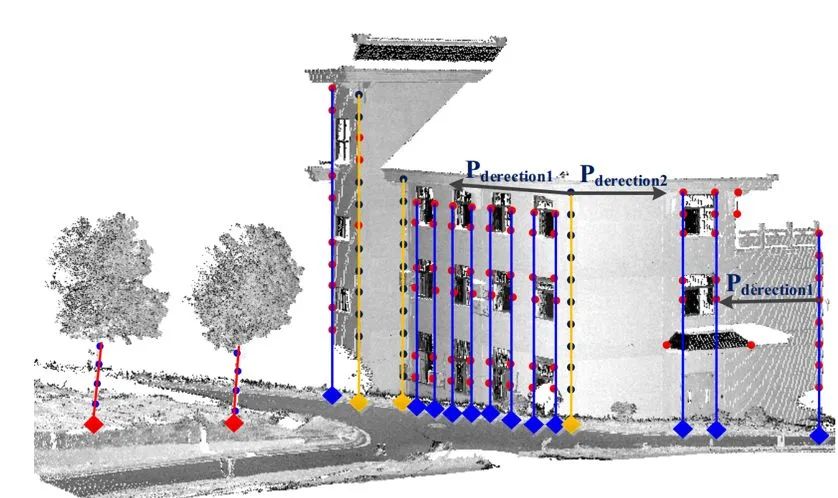
再将这些交点构建出三角形，以三角形的全等关系来得到匹配。

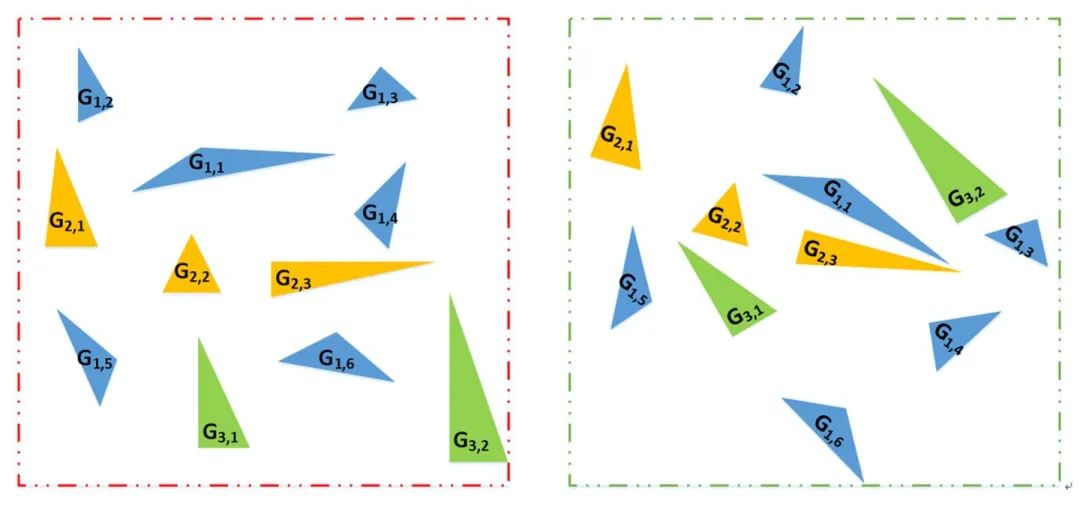
找出其中一致性最好的三角形集合，作为匹配的集合，进行粗配准。 这种方法适用于竖直线较多的场景，比如城区的建筑物的边线、林区树木的树干等。设计的方法还是很巧妙的。当然如果场景内这种特征较少，就比较难以配准。

编辑：黄飞