数字信号频谱带宽的上升时间F_3dB=0.35/Tr是怎么来的？

在一个 LTI 系统中，任何时域波形在频域中有等价的频谱 。这就意味着任一时域信号完全可以由频域参数来描述 。

它使电磁模型的频变性质同时域波形联系起来，从而我们就可以对总线上以数字比特传播的信号完整性进行分析 。时域信号以及其等价的频域描述的关系可由傅里叶变换进行描述：

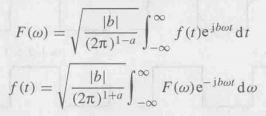
第一个式子将一个时域信号转换为了频域形式，而第二个将频域形式转换为了时域波形 。 傅里叶变换的惯例是基于 a与 b 的选择。常用的变换包括现代物理中的（ a＝0, b=-1 ），系统工程中的（ a＝1,b=-1），经物理中的（a＝1,b=1）以及信号处理中的（a＝ 0, b=2π）。

傅里叶变换通过将无限多的正弦函数进行叠加以得到原始的波形，简单地将时域波形同率响应联系了起来。例如，如果对一个占空 比为 50% 的方波进行傅里叶展开计算：

对于一个宽为两个时间单位的理想方波脉冲，如下图a所示，其频谱可以利用系统工程变换（a＝1,b=-1） 来计算得到：

上式为方波脉冲的频谱，如下图b，可以看到方波频域为一个sinc函数。

一个方波脉冲可作为一个数字比特的一阶逼近，但其更好的逼近为梯形波 。 如下图展示了一个梯形披同理想方波的频率响应的对比。

注意到梯形波频率响应的形状同方波是非常相似的，仅仅是谐波的幅度要小一些，在高频下这种现象更明显 。

这就说明了另一个重要概念：数字波形的上升与下降时间决定了其在频域范围内的高频诺波的幅度 。

上图同样说明了我们也可以通过在方波的频谱上外加一个低通滤波函数来得到一个梯形波的频谱。这样就可以定义出一个数字波形的谱分量同其上升与下降时间之间的关系 。

要得到这一关系，首先要来观察方波频谱自身的一些特点 。方波频谱函数表明方波的谐波为 sine 函数。对 sine 函数取极限就得到归一化的频谱：

一种得到近似梯形披频谱的方法是对方波的谐波外加一个低通滤披函数，直到能得到梯形波所描述的上升与下降时间 。

外加滤波器的最简单的方法是应用一个单极点低通滤披响应，比如 RC 网络。一个简单的单极点滤波器的阶跃响应为：

其中，Vinput为滤波器的输入电压，Vout为输出电压，τ为时间常数 。如果将上升时间用电压幅值的 10% 与 90% 来定义，那么就可以计算出具体的t10%~t90%下降一阶时所需的时间常数。当单位阶跃通过一个时间常数为τ的单极点滤波器时，其上升时间为

注意 t10%与t90%是分别由 0. 1=1-exp(-t10%/τ)和0. 9=1-exp(-t90%/τ)计算得出的 。单极点滤波器的 3 dB 带宽为：

则边沿谱分量与上升时间的关系式：

上式是数字信号频谱带宽的上升下降时间的较好粗略计算。

另外，更为普通的关系表达为：

对于高斯脉冲 K=0.338 对于单极指数衰减脉冲 K=0.350 对于大多数的数字信号 这0种小变化是没有什么关系的。