

排序算法之选择排序
描述
选择排序: (Selection sort)是一种简单直观的排序算法,也是一种不稳定的排序方法。
选择排序的原理:
一组无序待排数组,做升序排序,我们先假定第一个位置上的数据就是最小的,我们用一个参数记录这个最小的数,然后依次把后面的每个位置的数据和这个最小的比较,如果比这个数小就替换两个位置数据,等到第一轮比较完成就能确定最小的数据排在第一位了,然后第二轮从第二个位置开始,相同的方式比较,每次都能找到本轮最小的值,直至全部待排元素个数为0的时候,数组就排好顺序了。
选择排序流程图
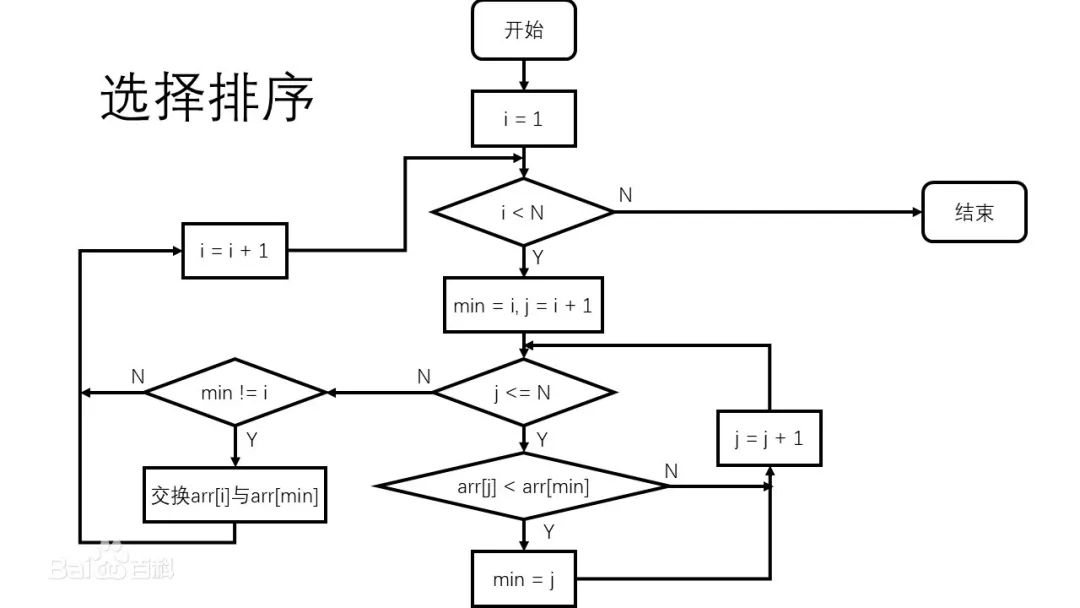
我们来进行详细解析看看
首先我们给个无序数组[4,6,15,9,12,3,32]进行升序排序,因为需要确定每个数组的长度,所以需要比较数组长度-1轮,当前面的元素都排好了之后,那么数组最后一个元素自然就确定了位置。
我们定义两个值,minIndex,minNum用来分别表示每一轮的找到的最小值的下标和值,后面未排序的值都和minNum比较,从而找出每一轮的最小值。
- 第一轮我们以下标为1的第一位作为标志位(也就是把第一个值当做最小值),那么此时minIndex=0,minNum=4,经过和 minNum 比较发现后面只有3比4小,那么3和4交换位置,minIndex=5,minNum=3,把4换到下标为5的位置,如下图所示:
 第一轮我们得到的结果是[3,6,15,9,12,4,32],本轮最小数是:3,所以3放到本轮标志位,也就是第一位
第一轮我们得到的结果是[3,6,15,9,12,4,32],本轮最小数是:3,所以3放到本轮标志位,也就是第一位
- 第二轮:拿到第一轮排序的值作为初始值[3,6,15,9,12,4,32],同第一轮一样,此时6作为标志位minNum=6,minNum和其他比较,只有4比6小,需要交换位置,如下图所示
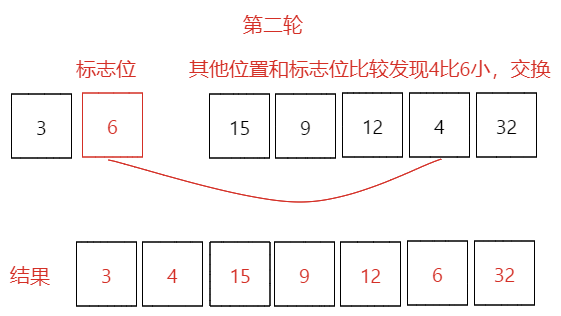 第二轮排序结果[3,4,15,9,12,6,32],本轮最小数是:4
第二轮排序结果[3,4,15,9,12,6,32],本轮最小数是:4 - 第三轮:初始值[3,4,15,9,12,6,32],这次标志位15,minNum=15,minIndex=2,minNum先比和9比较,发现9比15小,minNum=9,minIndex=3,然后minNum和12比较,不需要替换minNum,再和6比较,minNum=6,minIndex=5,后面再比较已经没有比6小了,那么本轮就是初始标志位15和下标为5,值为6的数据换位置。
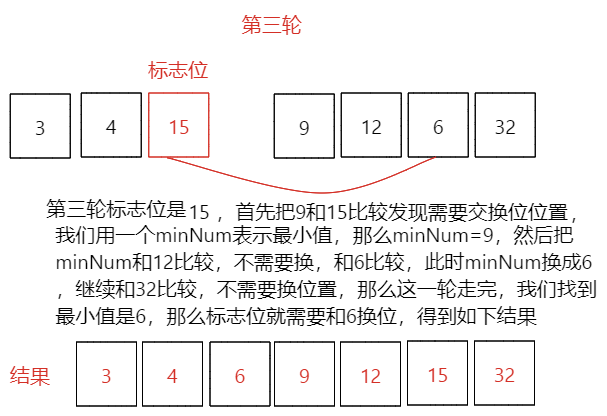
第三轮排序结果[3,4,6,9,12,15,32],本轮最小数是:6 - 第四、五、六轮:初始值[3,4,6,9,12,15,32],经过前面的比较我们可以看到数组已经排序完成,但是程序并不知道,会继续比较下去,把下标为4、5、6位置都作为标志位比较一次,发现都不需要变动位置,那么最终执行完成之后就能排序完成
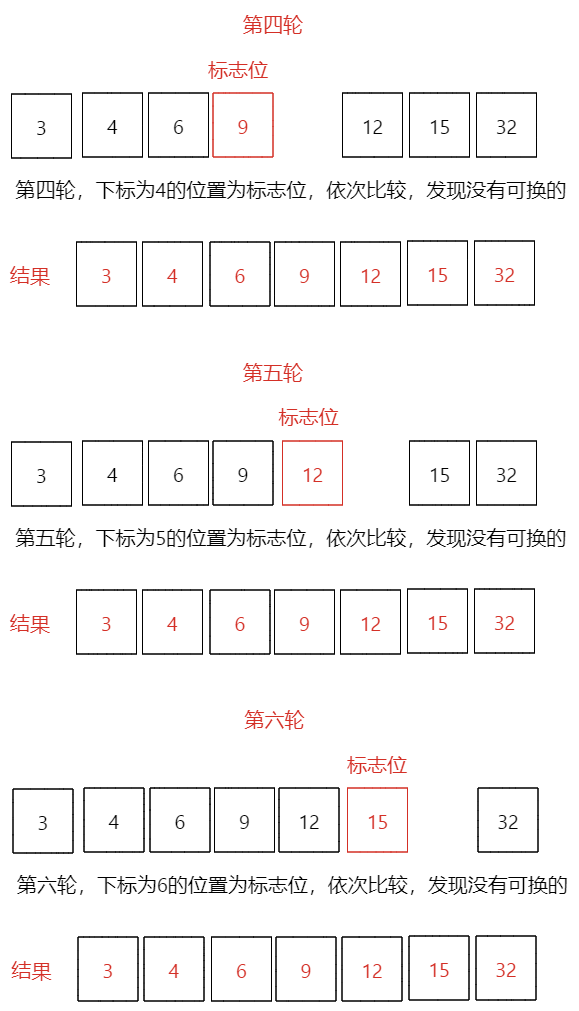 第四、五、六轮排序结果[3,4,6,9,12,15,32]
第四、五、六轮排序结果[3,4,6,9,12,15,32]
到这,我们已经清楚了每个步骤做了什么,那么接下来上代码验证一下:
Java代码实现
public class selectionSort {
public static void main(String[] args){
int[] arr = new int[]{4,6,15,9,12,3,32};
for(int i=0;i< arr.length-1;i++){//每次循环都会找出最小的数
//记录最小数的下标
int minIndex = i;
//记录最小数
int minNum = arr[i];
//每次循环都会找出最小的数
for(int j=i+1;j< arr.length;j++){
if(arr[j]< minNum){//如果当前数比最小数小,则更新最小数
minNum = arr[j];//更新最小数
minIndex = j;//更新最小数的下标
}
}
//将最开始假定的小的数移动到真实最小的位置
arr[minIndex]=arr[i];
arr[i]=minNum;//将标志位放到最小数原来所在的位置
//打印结果,方便查看
System.out.print("第"+(i+1)+"轮[");
for(int a=0;a< arr.length;a++){
System.out.print(arr[a]+"t");
}
System.out.println ("],本轮最小数是:"+minNum);
}
System.out.print("最终结果[");
for(int i=0;i< arr.length;i++){
System.out.print(arr[i]+"t");
}
System.out.println("]");
}
}
输出结果
第1轮[3 6 15 9 12 4 32 ],本轮最小数是:3
第2轮[3 4 15 9 12 6 32 ],本轮最小数是:4
第3轮[3 4 6 9 12 15 32 ],本轮最小数是:6
第4轮[3 4 6 9 12 15 32 ],本轮最小数是:9
第5轮[3 4 6 9 12 15 32 ],本轮最小数是:12
第6轮[3 4 6 9 12 15 32 ],本轮最小数是:15
最终结果[3 4 6 9 12 15 32 ]
时间复杂度
我们通过上面的细节拆分发现,无论是否是已经排好的还是没排好的情况,我们都需要每个数字都比较到,那么就出现N个元素的数组,第一轮是n次比较,第二轮是从第二个位置开始,那么就是n-1,第三轮就是n-2次... 最后是1,那么就出现了n+(n-1)+(n-2)+(n-3)...1,这是一个等差数列,求和为一个二次型多项式,因为等差数列求和会出现二次型;我们取最高阶就是n^2,所以时间复杂度就是O(n^2),而且最好和最坏的情况时间复杂度都是O(n^2)
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
十大排序算法总结2023-12-20 2095
-
FPGA排序-冒泡排序介绍2023-07-17 1617
-
常见排序算法分类2023-06-22 1683
-
浅谈希尔排序算法思想以及如何实现2021-06-30 2444
-
排序算法分享:归并排序说明2020-12-24 1146
-
详谈选择排序算法的定义和过程2020-06-30 4014
-
实用的排序算法 - 交换排序2020-03-20 2285
-
C语言中的排序算法了解2018-11-12 3106
-
常用排序算法分析2018-07-13 2582
-
常用的非比较排序算法:计数排序,基数排序,桶排序的详细资料概述2018-06-18 7709
-
常用的排序算法总览2018-06-13 3253
-
嵌入式stm32实用的排序算法 - 交换排序2018-04-12 8138
-
C语言教程之几种排序算法2017-11-16 1985
-
C语言冒泡、插入法、选择排序算法分析2013-09-06 606
全部0条评论

快来发表一下你的评论吧 !

 第二轮排序结果[3,4,15,9,12,6,32],本轮最小数是:4
第二轮排序结果[3,4,15,9,12,6,32],本轮最小数是:4
 第四、五、六轮排序结果[3,4,6,9,12,15,32]
第四、五、六轮排序结果[3,4,6,9,12,15,32]