

关于高速ADC在正弦输入时DNL测试结果的研究
电子说
描述
一 正弦波幅度分布的概率密度
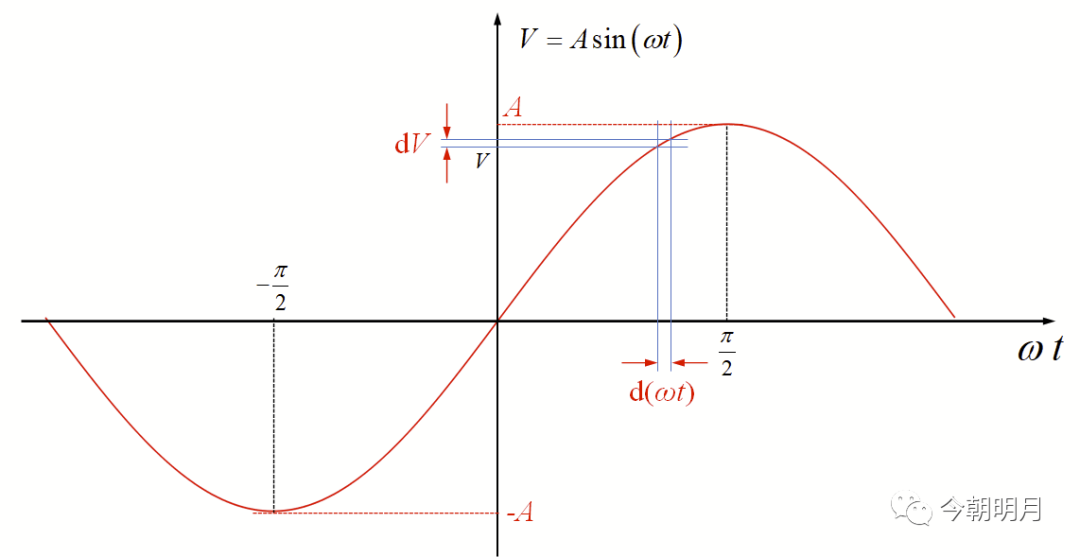
图1
所谓在正弦波取值范围(-A,A)内取到某个值V的概率密度p(V),是指取到V的某个邻域内的点的概率p(V,dV)与邻域宽度dV之比在dV趋向于0时的极限,即
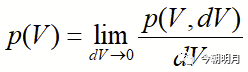
显然,p(V,dV)等于该邻域所对应的横坐标范围d(ωt)与全值范围(-A,A)所对应的横坐标长度π之比(如图1所示),即
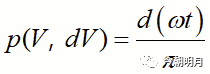
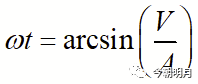
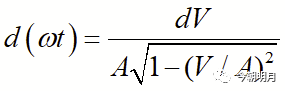
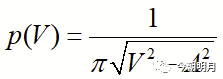
二 正弦波作为输入时ADC输出码的概率分布
取值在V1到V2之间的概率P(V1,V2)为
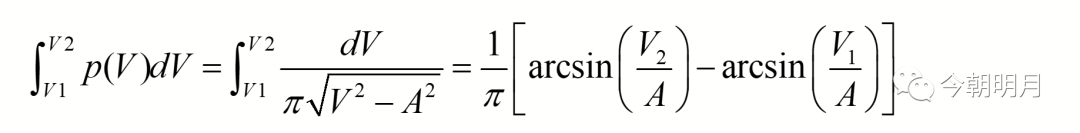
需要注意的是,在用上式计算概率时,务必使V1/A处于[-1,1]区间内。
对于理想的全差分ADC来说,假设输入信号范围为[-VREF,VREF],则输出码i∈[0~2^N-1]所对应的概率为
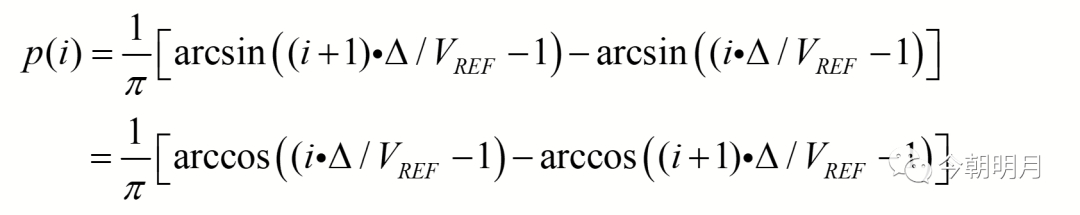
其中量化步长
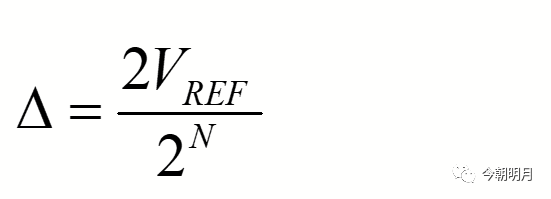 。
。
获得p(i)分布的matlab代码如下:

p(i)的分布图示例:(N=8,10,12,14)
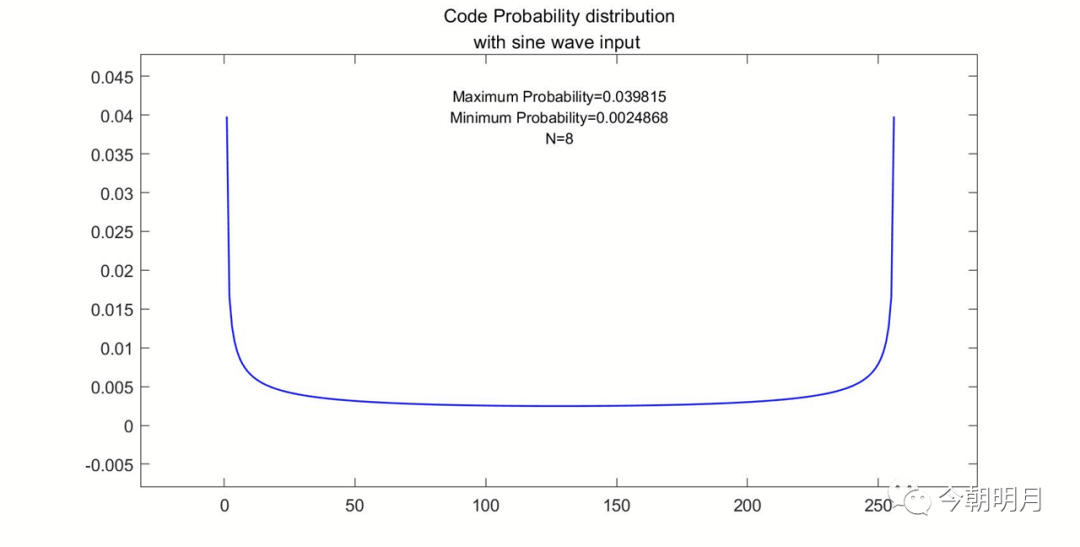
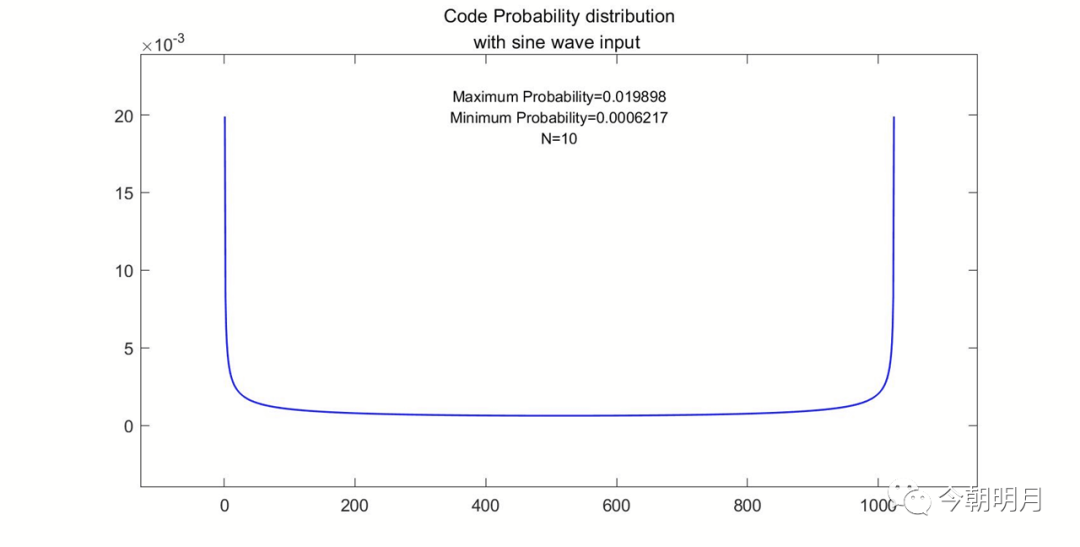
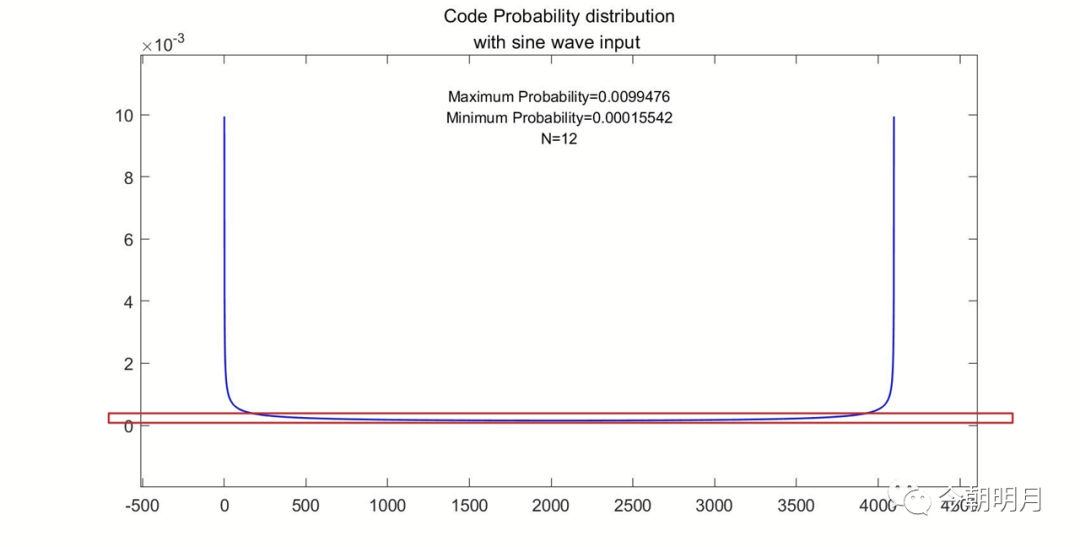
把上面红线部分拉开看
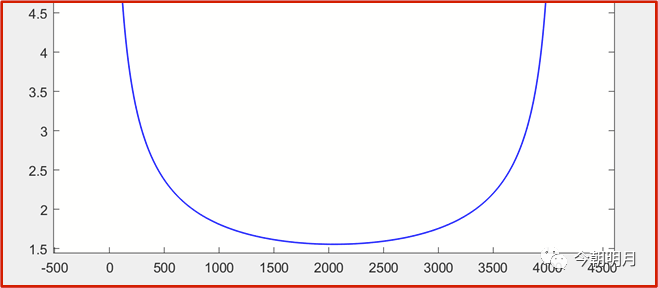
大写的Amazing!
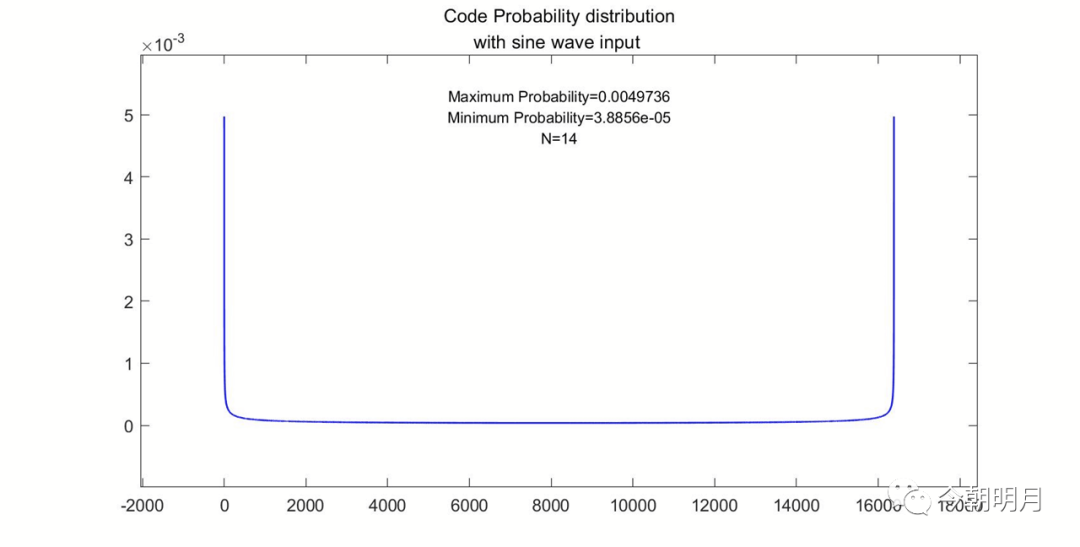
三 ADC DNL测试结果呈虹状弧线的理论解释
实际计算DNL时所用的公式为
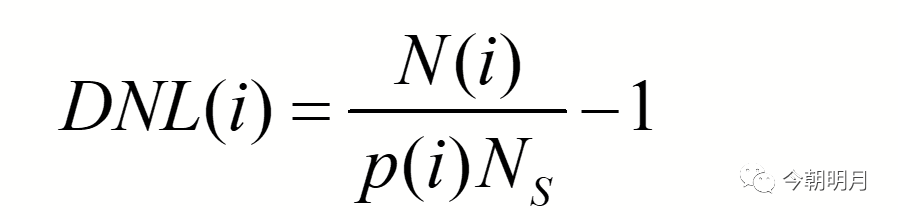
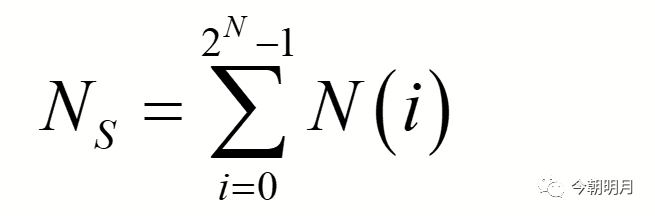
式中N(i)为实际得到的histogram中第i个code码出现的次数,即第i个bin的高度,NS为样本点的总数,p(i)Ns为第i个code出现次数的期望值(理想ADC code i应出现的次数)。由于噪声或其他因素导致每个bin的高度最有可能出现±1的误差,体现在DNL上的误差为:
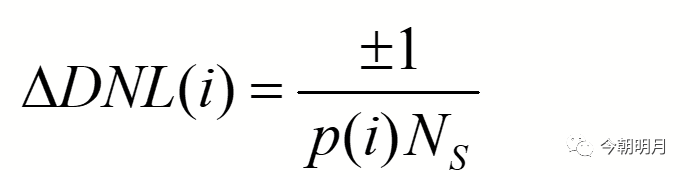
由code码概率分布可知,中间code出现的概率远小于两边code码的概率(例如N=12时,p(2^N-1)/p(2^(N/2)-1)=64;N=14时,p(2^N-1)/ p(2^(N/2)-1)=128!),因此 ΔDNL(i)也遵循着同样的规律,即中间最大,向两边递减,呈虹状弧线(如图X所示),并且随着Ns的增大,虹状弧线逐渐减小直至消失。
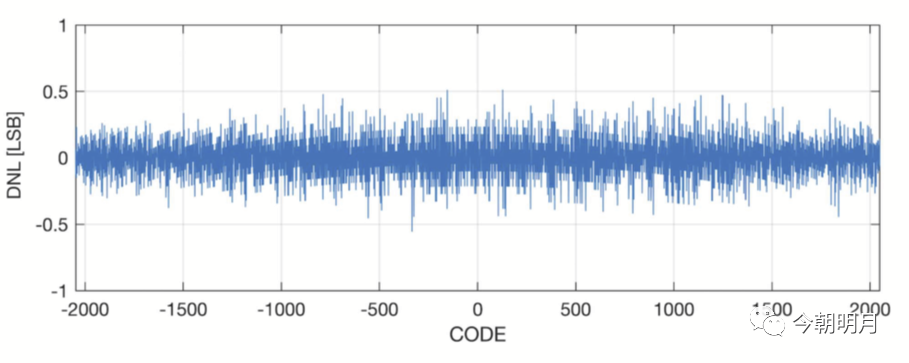
图X
四 实例演示样本点数对DNL图的影响
以一个12bit、切换方式为MCS的SAR ADC为例,作图演示样本点数分别为2^17、2^18、2^19时,DNL图样的变化:
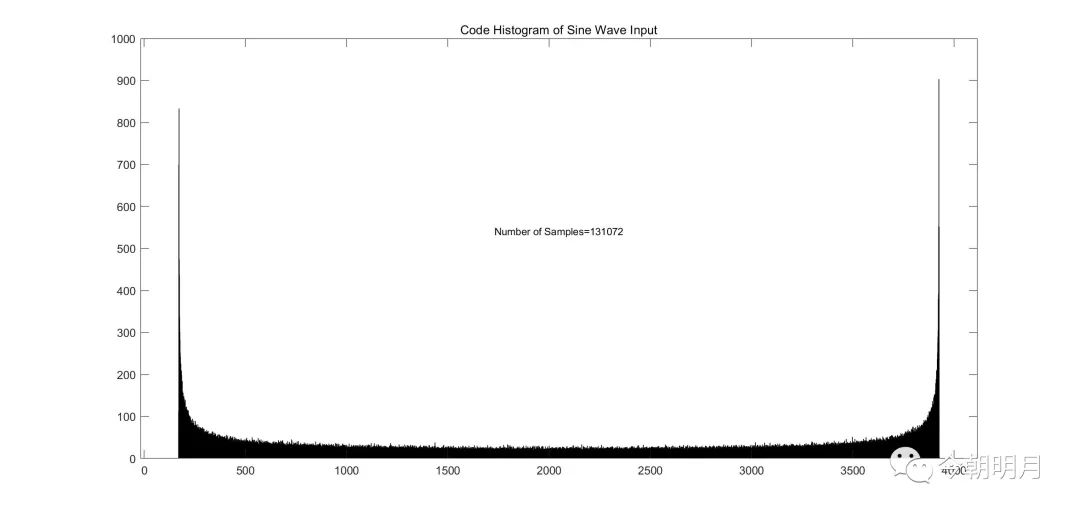
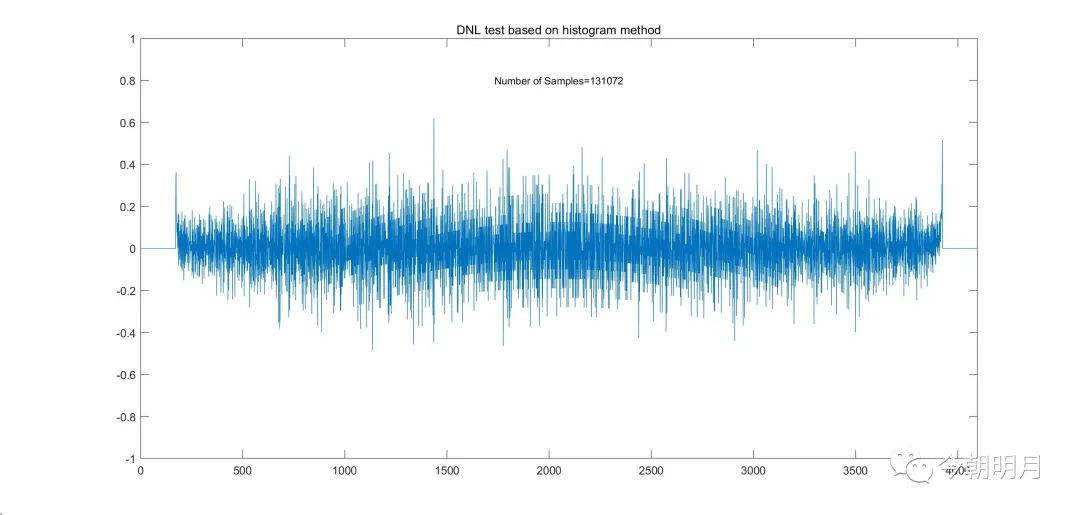
N=131072,虹状弧线明显
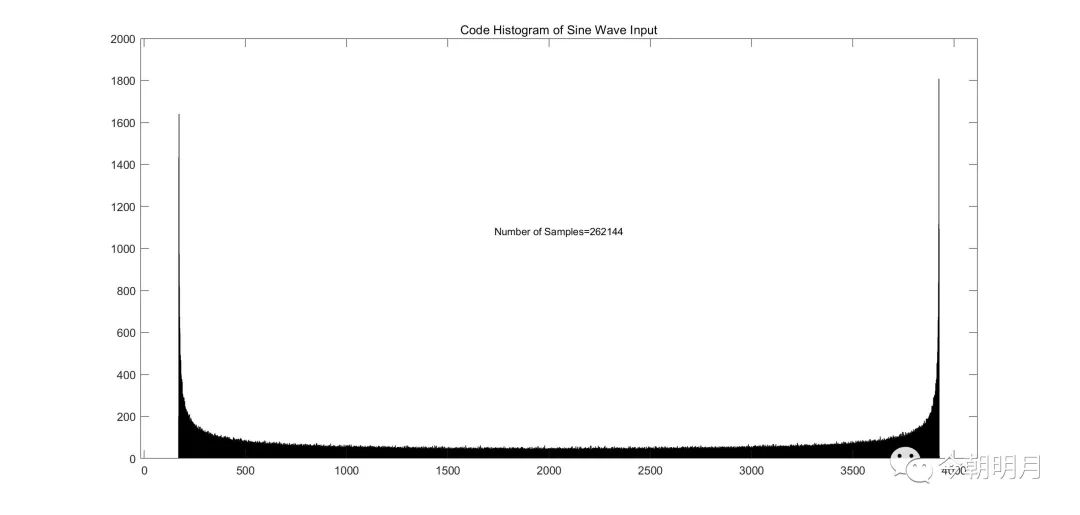
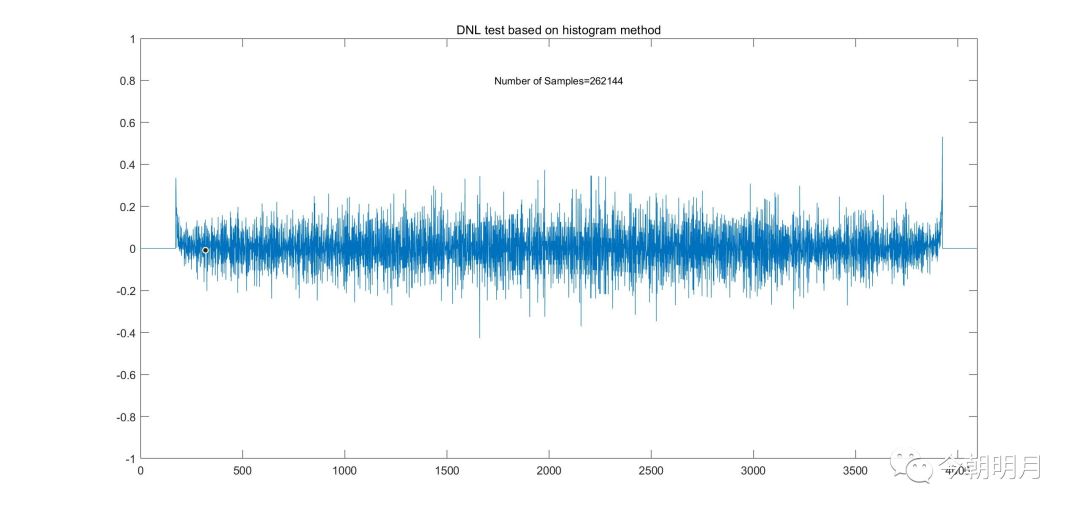
N=262144,虹状弧线减弱
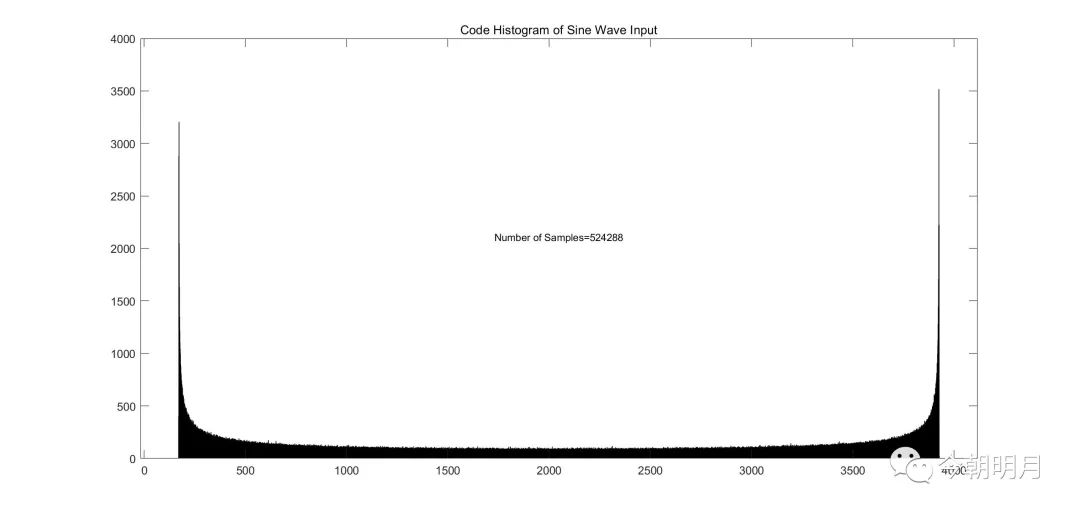
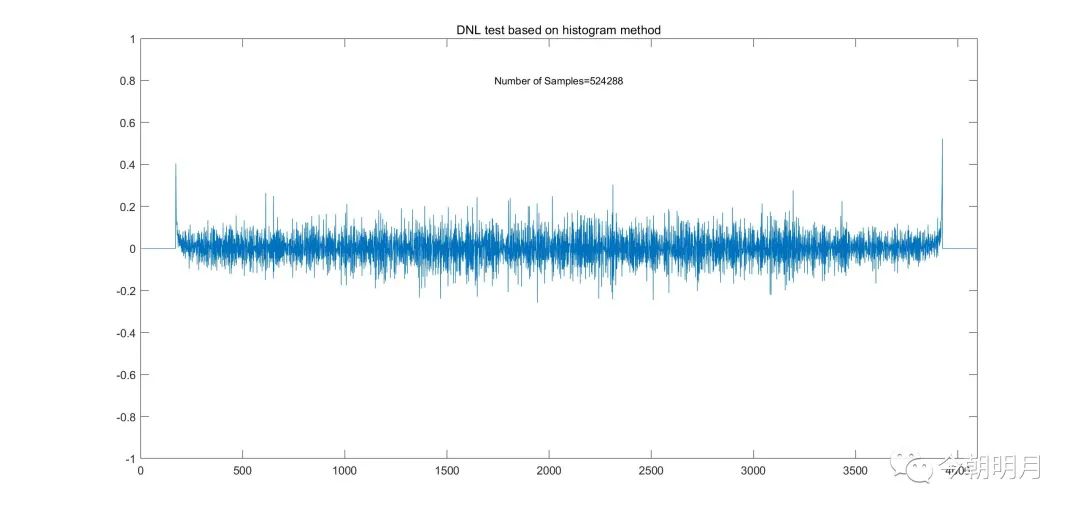
N=514188,虹状弧线基本消失
附 DNL作图代码
说明:出于知识产权,这里并没有加入DAC mismatch模型,而是在输入信号里加了高斯噪声以产生可观的DNL图像。
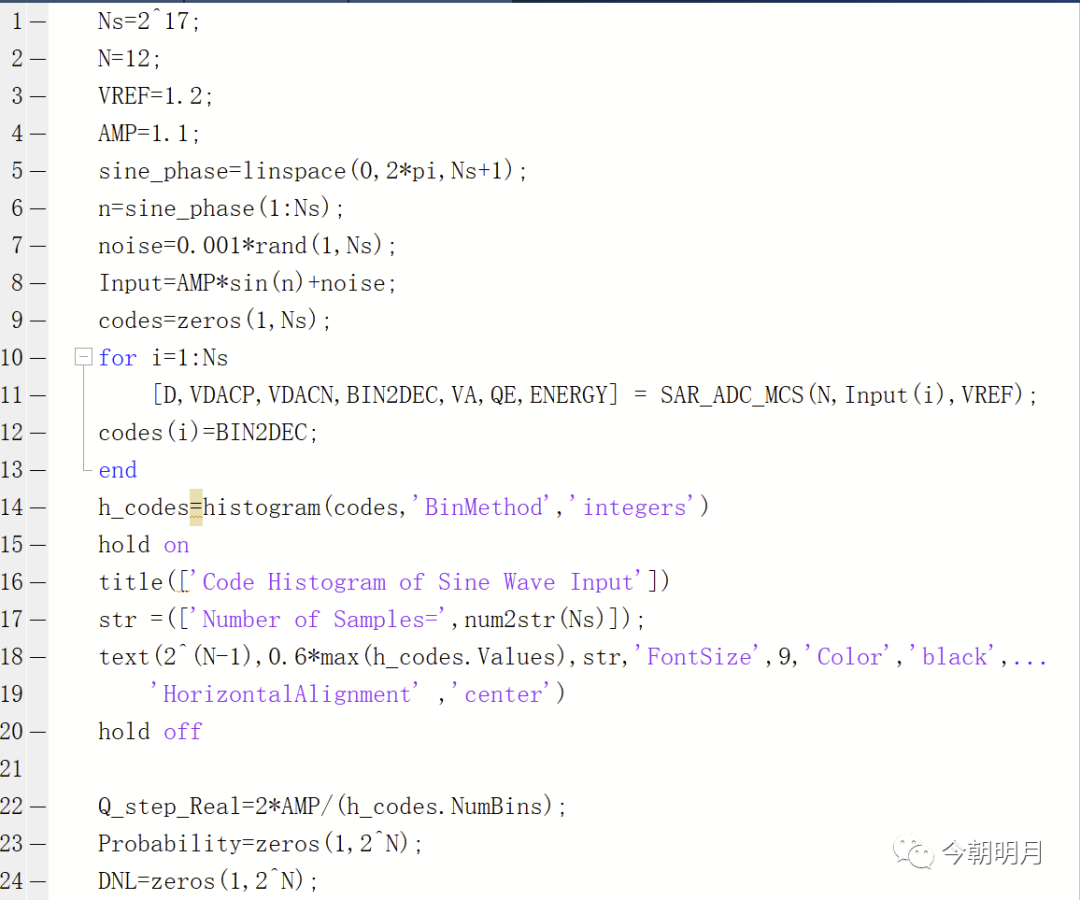

附 SAR ADC建模代码
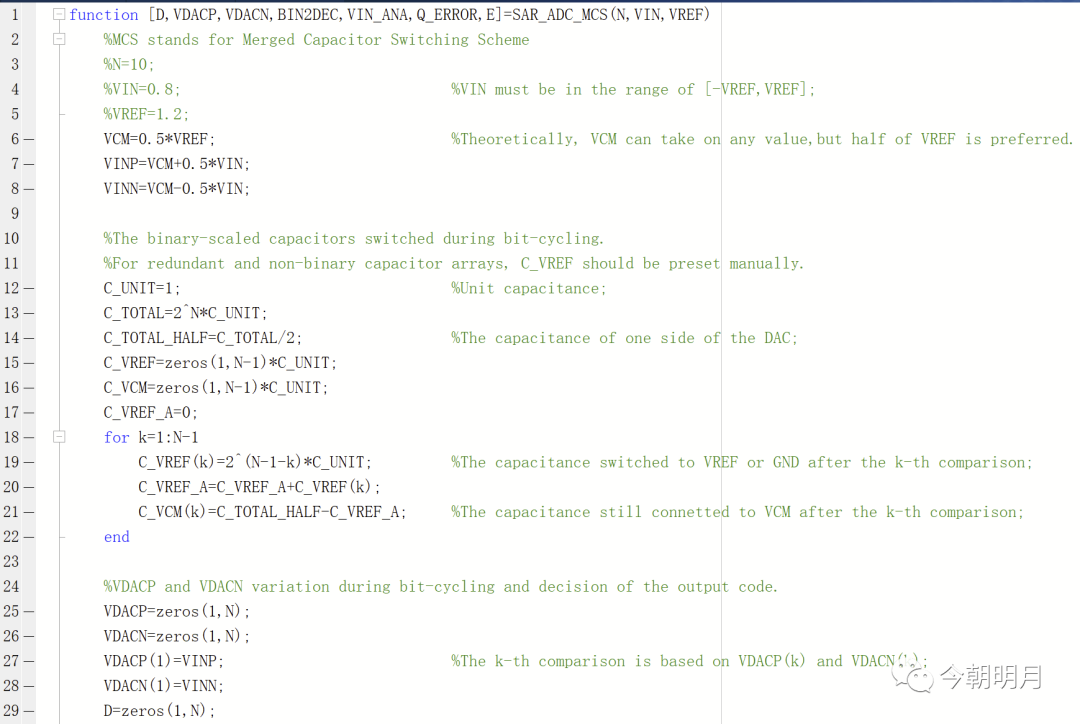


-
高速ADC/DAC的测试方法分享2023-11-07 7988
-
高速 ADC/DAC 测试原理及测试方法2018-04-03 10473
-
请问高速ADC或DAC输入时钟占空比如果不是50%或远高于或远低于50%对ADC或DAC性能有何影响?2018-08-16 3159
-
驱动ADC输入时简化设计流程的方法2018-09-19 1662
-
码密度法测试ADC的INL和DNL时输入正弦波的频率和采样频率,采样点有什么关系?2021-06-24 4321
-
ADC的输入时钟为多少2021-08-05 1341
-
高速ADC的驱动和输入网络的平衡2021-10-23 5255
-
ADC的微分非线性(DNL)和积分非线性(INL)规范解析2022-12-21 4599
-
如何测量高速ADC的INL和DNL2009-04-25 652
-
高速模数转换器(ADC)的INL/DNL测量2009-08-21 2318
-
adc转换器性能的动态测试2017-08-29 859
-
blog高速ADC、DAC测试原理及测试方法2021-09-17 1233
-
关于高速ADC测试和评估应用2022-07-04 1798
-
高速模数转换器的INL/DNL测量2023-02-24 9821
-
为成功的高速ADC正弦波测试选择最佳测试音调和测试设备2023-02-25 2819
全部0条评论

快来发表一下你的评论吧 !

