为什么离散实现不能提供高精度的电阻电流传感？

一个离散放大器和一些外部增益设置电阻器可以用来增加电流感测电阻器上的电压。虽然这种离散的解决方案可能是成本效益高，但由于外部组件的有限匹配，它们不能提供高精度。使用高精度电阻网络的尝试可以抵消使用简单离散解决方案可能带来的成本节约。

电阻电流传感的离散实现

在一个上一篇文章，我们讨论了基于运算放大器的非逆变结构可用于通过低侧电流检测电阻器来检测和提高电压。非逆变配置具有单端输入，并感测其相对于地的输入电压。这就是为什么我们不能在高侧感应配置中使用这个放大器。

另一方面，经典差分放大器具有差分输入。由于它感测并联电阻上的电压降，而不是节点对地的电压，因此它可用于低压侧和高压侧电流感应应用，如中所示图1

在这篇文章中，我们将讨论使用差分放大器时可能影响精度的两个重要误差源。

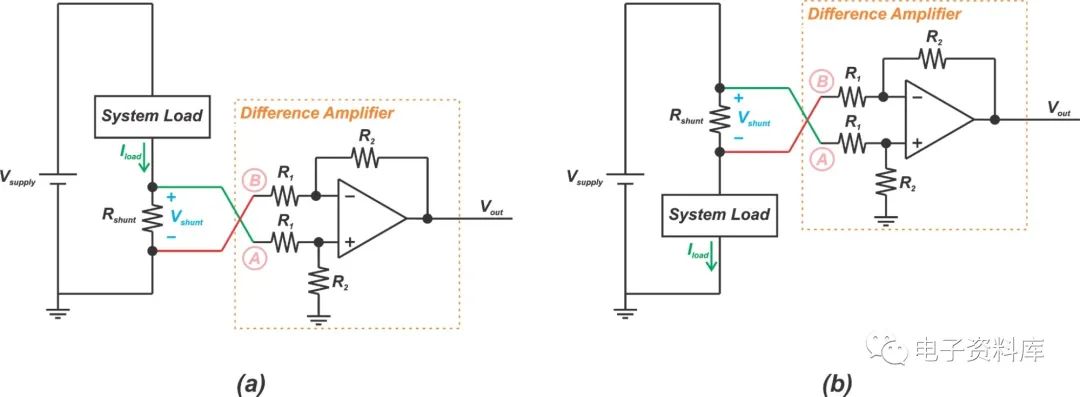
图1在（a）低压侧和（b）高压侧电流感应中使用差分放大器。

共模抑制比：一个关键特性

共模抑制比是差分输入放大器抑制两个输入共用信号的能力。放大器的传递函数可以表示为：

vout=Admvd+Acmvcvout=Admvd+Acmvc

方程式1

其中（A{dm}）和（v{d}）分别是放大器的差模增益和放大器输入处的差分信号。类似地，（A{cm}）和（v{c}）是应用于放大器的共模增益和共模信号。根据 方程式1 ，出现在放大器输出端的电压是输入共模值的函数。在 图1（b） ，我们理想地期望输出是差分信号V的函数分流器. 然而，实际上，输出也是电源电压V的函数供给 .

当我们改变V供给，放大器输入端的共模信号，因此，放大器的输出电压发生变化。即使我们保持V分流器不变的。为了减少这种非理想效应，我们需要使共模增益A厘米远小于差模增益Adm公司. 共模抑制比（CMRR）定义为差分增益除以共模增益，它规定了放大器在放大差分信号时抑制共模信号的能力。

离散实现的CMRR较低

考虑中所示的差分放大器图2 .

图2

对于理想运算放大器，差分放大器的传递函数由以下公式给出：

vout=R4R1×R1+R2R3+R4×vA−R2R1×vBvout=R4R1×R1+R2R3+R4×vA−R2R1×vB

For R2R1=R4R3R2R1=R4R3, we have:

vout=R2R1(vA−vB)vout=R2R1(vA−vB)

方程式2

该方程表明，任何共模电压都将被放大器完全抑制，即当vA=vBvA=vB时，我们得到vout=0vout=0。然而，在实践中，差分放大器的共模抑制将受到限制，因为比率r2r2r1不完全等于R4R3R4R3.它可以显示出来差分放大器的共模抑制比由下式给出：

CMRR≃Ad14tCMRR≃Ad14t

方程式3

式中（A{d}）是差分放大器的差分增益，其等于（frac{R{2}}{R}{1}}}）；t是电阻公差。例如，当微分增益为1和0.1%电阻器时，我们有：

CMRR≃Ad+14t=1+14×0.001=500CMRR≃Ad+14t=1+14×0.001=500

用dB表示这个值，我们得到一个大约54 dB的CMRR。请注意方程式3在假设运算放大器是理想的且具有很高的共模抑制比的前提下推导出来的。如果运算放大器的CMRR不远大于从方程3得到的值，我们需要使用更复杂的方程 .

集成解决方案可导致较高的CMRR

因此，即使有一个理想的运算放大器，差分放大器的共模抑制比也相对较低，并且受到增益设置电阻匹配的限制。

为了解决这个问题，我们可以使用一组匹配的电阻网络，例如 LT5400型. LT5400是一个四电阻网络，匹配率为0.005%，可用于创建具有高共模抑制比的差分放大器，如中所示 图3 . 使用匹配的电阻网络，一个约80分贝的共模抑制比应该是可以实现的。

图3电阻阵列可以用来制造具有极高共模抑制比的差分放大器。图片由线性技术.

一个离散放大器和一些外部增益设置电阻可以被认为是一个低成本的电流测量解决方案。然而，正如你所见，增益设置电阻的匹配决定了放大器的共模抑制比。尝试使用一个单独的高精度电阻网络可以抵消使用一个简单的差分放大器可以节省的成本。

我们可以使用完全单片的解决方案，如AMP03从模拟设备集成激光微调电阻到精密运算放大器封装，以实现电阻之间的高匹配。这种集成解决方案可以获得大于100db的CMRR。

另一个错误来源：增益设定电阻的温度漂移

增益设定电阻的温度漂移是影响测量精度的另一个因素。如上所述，增益设置电阻的公差决定了放大器在室温下的初始精度。然而，为了使电阻比保持恒定，电阻器在工作温度范围内应表现出类似的行为。

让我们考虑一下如何产生温度漂移的例子。假设电阻值方程式2are R1=5 kΩ and R2=100 kΩ. 此外，假设电阻器的温度系数为±50 ppm/°C，环境温度可比参考温度（室温）高100°C。

微分增益的最大值和最小值是多少？

高于参考温度的100°C温升可使±50 ppm/°C电阻器的值变化±0.5%。因此，最大微分增益由下式得出：

Adm,max=R2,maxR1,min=100×(1+0.005)5×(1−0.005)=20.20Adm,max=R2,maxR1,min=100×(1+0.005)5×(1−0.005)=20.20

最小增益通过以下方式获得：

Adm,max=R2,minR1,max=100×(1−0.005)5×(1+0.005)=19.80Adm,max=R2,minR1,max=100×(1−0.005)5×(1+0.005)=19.80

注意，电阻器可能朝相反方向漂移。在这个例子中，1%的增益误差是由漂移效应引起的，因为我们假设电阻在室温下有其标称值。

有趣的是，与匹配的电阻网络，如 LT5400型或者是一个完全单片的电流检测解决方案，集成电阻可以表现出几乎完美的匹配，这两个初始误差和温度漂移。如中所示图5 .

图5图片由威世半导体.

在本图中，橙色线规定了温度从基准温度（20°C）向任一方向变化时单个±50 ppm/°C电阻器值变化的限值。红色曲线表示匹配电阻阵列的四个集成电阻器的温度行为。

当来自匹配电阻网络的单个电阻器的温度系数为±50ppm/°C时，四个集成电阻器的温度行为非常匹配。随着温度的变化，电阻值互相跟踪。这些匹配的电阻允许我们保持放大器增益在工作温度范围内相对恒定。

结论

一个离散放大器和一些外部增益设置电阻器可以用来增加电流感测电阻器上的电压。虽然这种离散的解决方案可能是成本效益高，但由于外部组件的有限匹配，它们不能提供高精度。

增益设定电阻的匹配决定了放大器的共模抑制比。为了获得高的共模抑制比，需要使电阻的初始误差和温度漂移达到近乎完美的匹配。

这就是为什么在CMRR方面，集成解决方案可以轻松击败离散实现。请注意，尝试使用单独的高精度电阻网络可以抵消使用简单离散解决方案可能带来的成本节约。