为什么要引入S参数？S参数-传输线测试分析利器

一．为什么要引入S参数

S参数的全称为Scattering 参数，即散射参数。微波系统主要研究信号和能量两大问题：信号问题主要是研究幅频和相频特性；能量问题主要是研究能量如何有效地传输。微波系统是分布参数电路，必须采用场分析法，但场分析法过于复杂，因此需要一种简化的分析方法。

微波网络法被广泛运用于微波系统的分析，是一种等效电路法，在分析场分布的基础上，用路的方法将微波元件等效为电抗或电阻器件，将实际的导波传输系统等效为传输线，从而将实际的微波系统简化为微波网络，把场的问题转化为路的问题来解决。

微波网络理论是在低频网络理论的基础上发展起来的，低频电路分析是微波电路分析的一个特殊情况。一般地，对于一个网络，有Y、Z和S参数可用来测量和分析，Y称为导纳参数，Z称为阻抗参数，S称为散射参数；前两个参数主要用于集总电路，Z和Y参数对于集总参数电路分析非常有效，各参数可以很方便地测试；但是在微波系统中，由于确定非横电磁波（TEM）电压、电流非常困难，而且在微波频率测量电压和电流也存在实际困难。

因此，在处理高频网络时，等效电压和电流以及有关的阻抗和导纳参数变得较抽象。与直接测量入射、反射及传输波概念更加一致的表示是散射参数，即S参数矩阵，它更适合于分布参数电路。

S参数就是建立在入射波、反射波关系基础上的网络参数，适于微波电路分析，以器件端口的反射信号以及从该端口传向另一端口的信号来描述电路网络。同N端口网络的阻抗和导纳矩阵那样，用散射矩阵亦能对N端口网络进行完善的描述。

阻抗和导纳矩阵反映了端口的总电压和电流的关系，而散射矩阵是反映端口的入射电压波和反射电压波的关系。散射参量可以直接用网络分析仪测量得到，可以用网络分析技术来计算。只要知道网络的散射参量，就可以将它变换成其它矩阵参量。

二．典型二端口网络的S参数

二端口网络是指有一个输入口Port1和一个输出口Port2的无源电路网络。对于线性无源二端口网络，从端口出去的正弦信号一定与进去的正弦信号同频率。

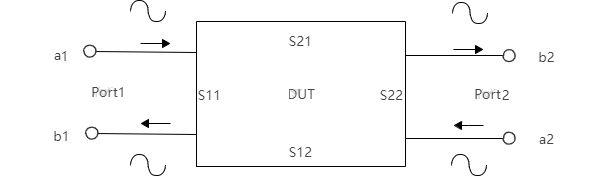
二端口网络共有四个S参数，分别为S11、S12、S21和S22，各参数的物理含义和特殊网络的特性如下：

S11 = b1/a1，端口2匹配时，端口1的反射系数；S22 = b2/a2，端口1匹配时，端口2的反射系数；S12 = b1/a2，端口1匹配时，端口2到端口1的反向传输系数；S21 = b2/a1，端口2匹配时，端口1到端口2的正向传输系数。S参数具有对称性，即如果传输通道完全对称则S11=S22；S21=S12。

信号关系如下：

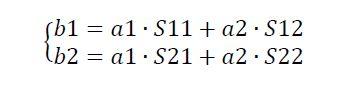
即：

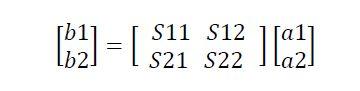
三．S参数特性

S参数的三大特性：无源性，互易性，因果性。

无源性：对于一个无损网络，S矩阵是一个单位矩阵，对于二端口网络存在下面关系式：| S11 |²+| S11 |²=1，由于没有损耗，所以散射的总量是100%。当S21大的时候，S11就会小一些。对于无源的二端口的网络, | S11 |²+| S11 |²<1，因此一个无源器件的S参数不会大于1（0dB）。

互易性：如果一个器件是可交换方向使用而不是单相的，如隔离器、环行器，S矩阵是对称的，因此，Sij=Sji。也可以说是从通道两侧分别看过去，它的特性应该是一致的。

因果性：因果性指的是先有激励才有输出。对于无源系统的S参数，由于信号的传输一定会产生相应的延时，因此无源系统的S参数应该符合因果性原理的。但实际测得的S参数往往会由于种种原因产生一定的非因果性，导致不正确的仿真结果。

S参数不满足三要素就会导致结果不准确，这是就需要从新提取S参数，例如调整网格划分和收敛值，重新提取即可。

四．S参数的信号完整性分析应用

根据信号的频域特性，任何信号都可以拆解为一系列不同频率的正弦波的叠加。随着频率的不断增加，高频频点的正弦波信号传输到接收端的信号能量将逐渐减少，而S参数恰恰能够清晰的描述各个频点的正弦波通过互连导通后的衰减情况，采用S参数不仅可以分析导通对信号的影响，还可以根据需要进行补偿一些衰减比较严重的高频频点。

S参数与信号完整性有着密切联系，其中S11能够反映信号反射及阻抗匹配问题，S21能够反映信号的传输特性。

此外，利用S参数还能够直接得到介质材料的相对介电常数、介质损耗等参数信息，这是一般的时域分析所不具备的。因此可见，S参数可以很好地分析信号完整性问题。