

一个问题后面的理论-互易定理解析
描述
十一假期期间,又被号友整了个灵魂一问。
然后号友,就甩给我一篇他们大牛老师的手写讲义。
我一看,顿时头昏脑胀,这还没看到上面的公式,光看上面的字,就已经云里雾里,完全看不懂。
比如说,下面~
这不就和我们看医生的时候,医生写的病例一样嘛,自带加密效果,普通人根本看不懂。
不过,老师的弟子,还是能看懂的,他把那句话给我翻译了一遍,然后我一个词一个词对应上去,发现确实是这么些单词。
我平生,测过的一个天线,就是当年研究生论文的时候,仿真的那个。当时,是在学校的暗室进行测试的,过去后,就按照实验室老师的要求,摆放天线,然后实验室老师就在暗室外面操作电脑,我们就拿着U盘把测试结果拷过来,也没太深究原理。当时也没有讲究,这个天线是用在发射,还是用在接收。
所以,我又把这灵魂一问,甩给了一位做天线十几年的朋友。
大意就是,对于无源天线而言,不管是用于发射,还是接收,方向图是一样的。
理论原理
今天看微波工程的时候,发现在1.9章中的互易定理(reciprocity theorem)中描述的公式,和号友老师的手写讲义中的公式差不多。
以前看到这章的时候,直接就略过去了,感觉在实际工作中好像没怎么涉及过。
不过现在看来,还是自己想的不深入。就如号友问的这个关于收发天线的方向图的问题,后面就隐藏着一个理论。
想着大牛老师的讲义上的字看不懂,但是微波工程中的字,我能看懂哈。
所以就又看了一遍。
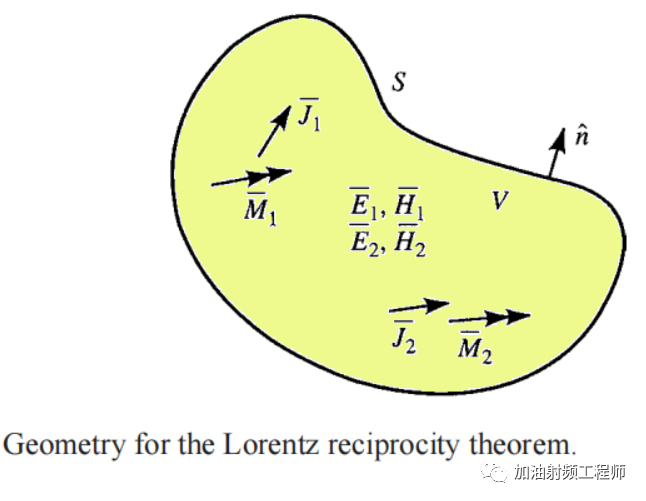
假设在体积V里面,有两个单独的源的集合,分别为(J1,M1)和(J2,M2),这些源产生的场分别为(E1,H1)和(E2,H2)。而且,体积V由闭合曲面S包围。
这两组源和场,分别满足麦克斯韦方程,如下图所示:
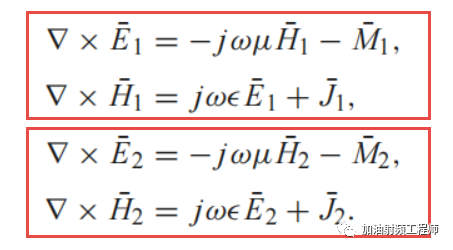

然后由散度定理可知,又可进一步得到:

如果S,是无穷远处的一个闭合曲面。此时闭合曲面处的场离源非常远,所以局部可以看成平面波。
此时,可以得到:

对于平面波,有:
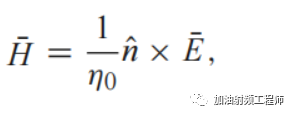
又:
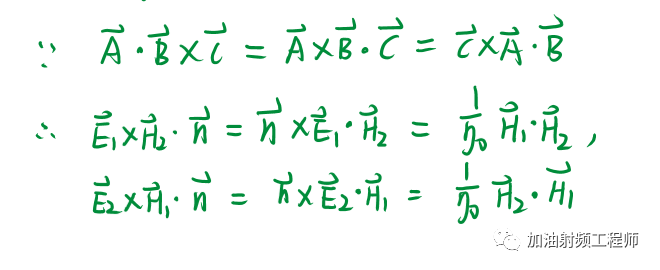
所以可以得到:

如果不考虑磁流源,即M1=M2=0,则:
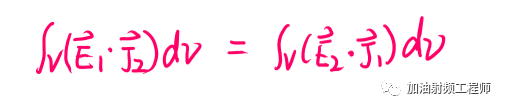
上面的式子,表示,当源和观测点互换时,观测到的场E1或者E2没有变化。
正是基于上面的互易理论,同一天线,作为发射天线或者接收天线时,具有相同的辐射方向图。
审核编辑:刘清
-
电路互易定理的使用条件2015-09-27 7527
-
特勒根定理和互易定理2008-12-08 1432
-
电路定理教案(PPT讲稿)2009-07-08 368
-
互易双口和互易定理2010-08-26 1086
-
互易定理2010-08-25 5983
-
基于抽样定理及信号恢复理论证明2017-12-25 973
-
普遍n口网络的等效电压源定理2018-01-23 1417
-
戴维南定理典型例子_戴维南定理解题方法2018-03-14 231308
-
动能定理公式的理解与推导2018-03-16 42379
-
电路的互易定理2018-08-22 27115
-
声波互易定理被打破 自动驾驶车辆通信得到改善2020-03-24 3235
-
电路经常使用的定理详细介绍2020-10-12 1216
-
CAP 定理:理论、实践2024-08-19 1130
-
运放型号后面的am代表什么2024-09-23 2033
全部0条评论

快来发表一下你的评论吧 !

