

如何表达晶体取向?介绍一下晶体取向的图形表示法
描述
实际样品中,并不能直接观察到不同的晶体学方向或晶面,只能看到晶粒的形貌。这就要求确定晶体的不同方向与宏观样品可观察到的特征方向间的关系,简言之,就是要确定晶体坐标系与外界样品坐标系的关系,这就是取向的概念。
晶体取向的表示方法通常有数字表示方法(如密勒指数、矩阵等)和图形表示法。
本篇推文主要给大家介绍一下晶体取向的图形表示法。
01
取向用极图表示
极图是表示某一取向晶粒的某一选定晶面{hkl}在包含样品坐标系方向的极射赤面投影图上的位置的图形。例如,一个取向的{100}极图是将该取向的晶胞的3个{100}晶向的极射赤面投影位置表示出来,见下图:
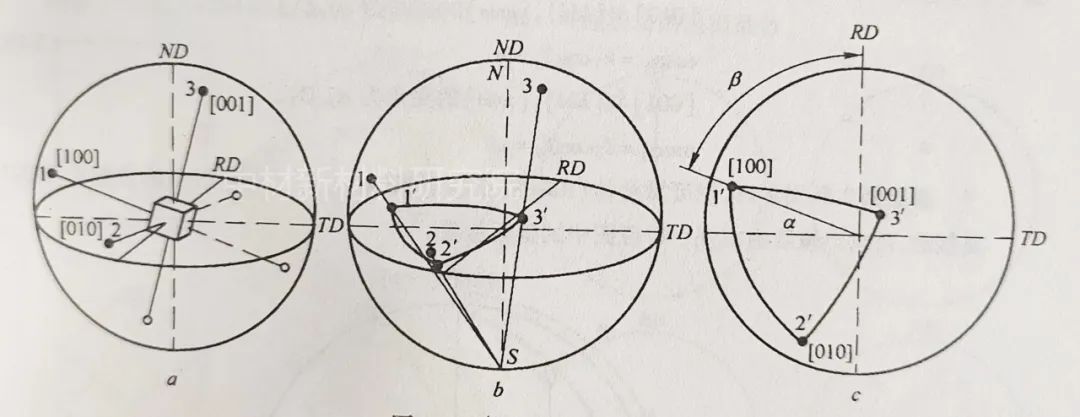
其基本过程是:小单胞处在参考球中心,其任意的方位表示其对外界参考系(RD-ND-TD)的取向,这时其(hkl)面平行于轧面(RD-TD组成),其[uvw]平行于RD。
现在要用3个{100}极点表示单胞相对于样品坐标系的取向,即看它的3个{100}点在极图上的位置。
由3个{100}点的位置,应可联想其单胞的空间方位。当然,这需要反复的练习。
当用图c中的极角α,β表示极轴r在样品坐标系下的坐标时(α是极轴r与ND的夹角,β是极轴r在轧面上的投影线与RD的夹角),r可表达为:
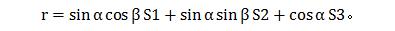
S1,S2,S3是RD,TD,ND方向的单位矢量。
同时r又可在晶体坐标系下表达为:
r=xc1+yc2+zc3。
c1,c2,c3是[100][010][001]方向的单位矢量,(x,y,z)经过了归一化处理。
这时,极轴的极角r坐标(α,β)、晶体坐标(x,y,z)和取向矩阵gij的关系为:
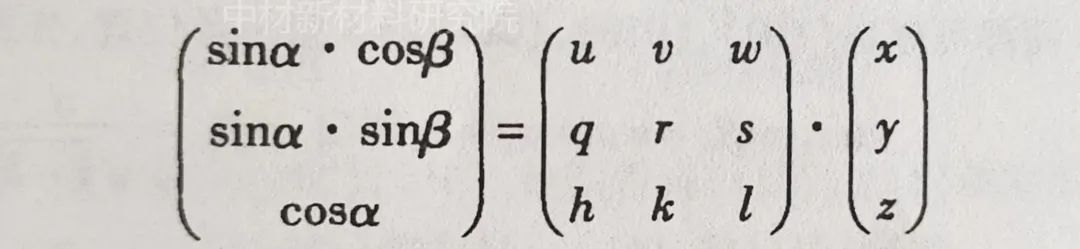
从上式可求出极轴(x,y,z)在极图上的位置。
另外要注意的是,求出的极角(α,β)用吴氏(Wulff)网标在极图中就是极射赤面投影图,也就是最常用的极图。若用Schmid网标在极图中就是等面积投影图。
02
反极图
与极图相反,反极图是描述多晶体材料中平行于材料的某一外观特征方向的晶向在晶体坐标架的空间分布的图形,参考坐标架的3个轴一般取晶体的3个晶轴(或低指数的晶向)。
作反极图时将设定的外观特征方向(如ND)的晶向标于其中,从而反映该外观特征方向在晶体学空间的分布。
类似极图中两个坐标系下取向矩阵与极角和极轴的关系,反极图下也有下列关系:
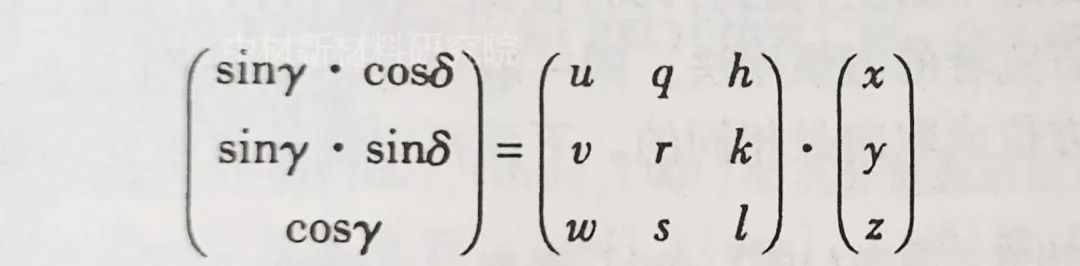
(x,y,z)是某一晶轴r在样品坐标系(RD,ND,TD)中的坐标。(δ,γ)是r在晶体坐标系[100]-[010]-[001]构成的极图中的极角坐标。这里使用的是取向矩阵,而不是逆矩阵。
严格来讲,反极图也应用大圆表示,但通常用以<100>-<110>-<111>组成的取向三角形表示。这是将取向对称化处理的结果。否则[-100]方向是用[001]-[101]-[111]取向三角形表示不出来的。
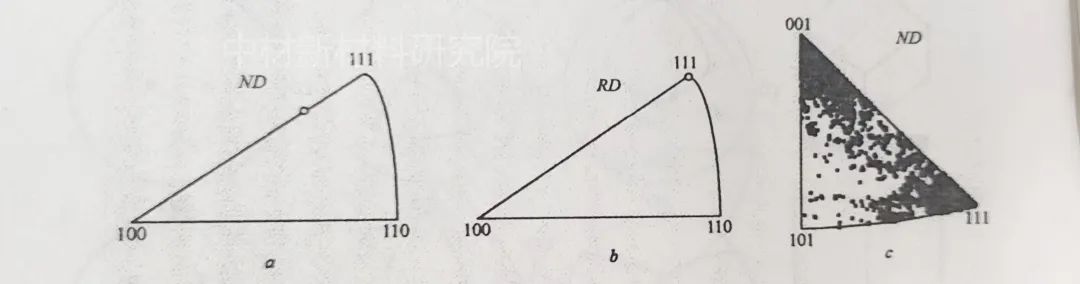
铜型取向(112)[11-1]。要用两个反极图表示,见上图a,b。这里RD=[11-1]是等效表示。因为一个反极图中只能标出一个方向。图c为热压缩刚等距离测出的400个取向的反极图表达,只标出每个取向中ND方向的分布。多数晶粒已转到<001>和<111>取向。
03
欧拉取向空间的表示
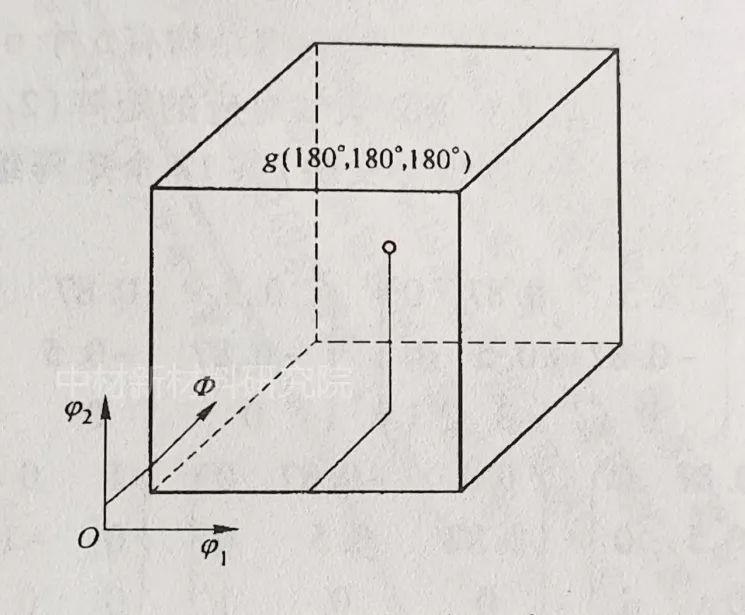
欧拉角表示3个转动,范围是(0~2π)、(0~2π)、(0~2π),显然具有周期性,即:g=f(ψ1,Φ,ψ2)=f(ψ1+2π,Φ+2π,ψ2+2π)。但还存在关系:f(ψ1,Φ,ψ2)==f(ψ1+π,2π-Φ,ψ2+π),即在Φ等于π时存在一个镜面对称性。因此,欧拉空间范围是(0~2π)、(0~π)、(0~2π)。晶体对称性和样品对称性会进一步减小欧拉空间范围。
对立方晶系中的铜取向(90,35,45),如下图所示:虽然简单,但不如二维图形表达得直观易懂。
欧拉取向空间的表示
04
罗德里格斯矢量
罗德里格斯矢量或角轴对都是三维矢量,也可以用图形表示。对单个角轴对,轴的位置可用类似反极图的取向三角形表示,角度只是一个数字,不需要用图形表示。而R矢量要表示在罗德里格斯空间中。这两种取向表示方法更适合描述晶粒间的取向差分布。
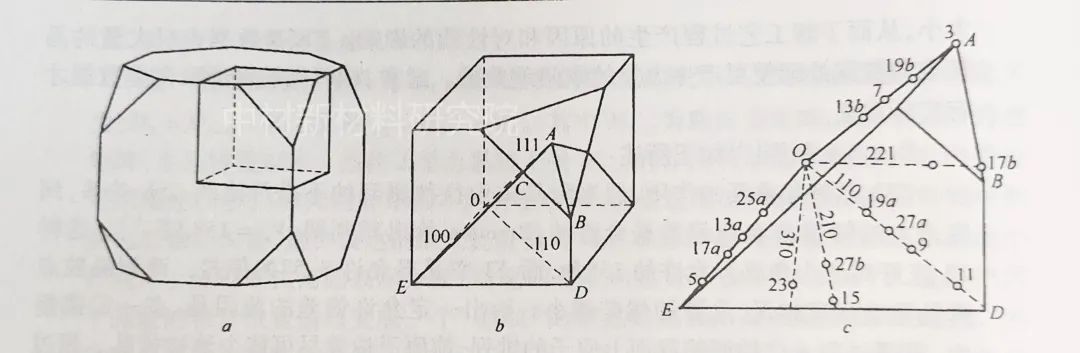
立方结构晶体的R空间(a)及简化空间(b)
最小单元体是原立方体的1/48 (c)
审核编辑:刘清
-
什么是取向材料?2018-11-27 2510
-
晶体管的分类与特征2018-11-28 2585
-
晶体管如何表示0和12021-01-13 3950
-
MVA(多畴垂直取向)广视角技术的原理分析2008-07-16 3383
-
国内首颗无机取向LCOS芯片实现量产2020-12-06 2810
-
无取向硅钢在新能源汽车应用现状及前景2021-05-19 1211
-
LiNbO3刻蚀速率与晶体取向的关系2021-12-24 1487
-
浅谈1nm晶体管后,更复杂的单片CFET有效替代方案2022-07-10 1091
-
TiO2纳米晶体的晶体取向和暴露面到底是怎样的?2022-08-25 7487
-
取向冷轧硅钢铁芯对变压器性能的影响2022-12-05 1684
-
氮化镓晶体管的优点2023-02-08 1349
-
多晶体的塑性变形与细晶强化简析2023-08-11 3680
-
石英晶体切割类型与频率的关系2024-07-22 1577
-
晶体取向反极图实验数据的采集方法2024-11-05 2060
-
电子背散射衍射晶体学织构分析与数据处理2025-01-07 1659
全部0条评论

快来发表一下你的评论吧 !

