排序算法有哪些

1. 归并排序（递归版）

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治策略，即分为两步：分与治。

1. 分：先递归分解数组成子数组
2. 治：将分阶段得到的子数组按顺序合并

我们来具体看看例子，假设我们现在给定一个数组：[6，3，2，7，1，3，5，4]，我们需要使用归并算法对其排序，其大致过程如下图所示：

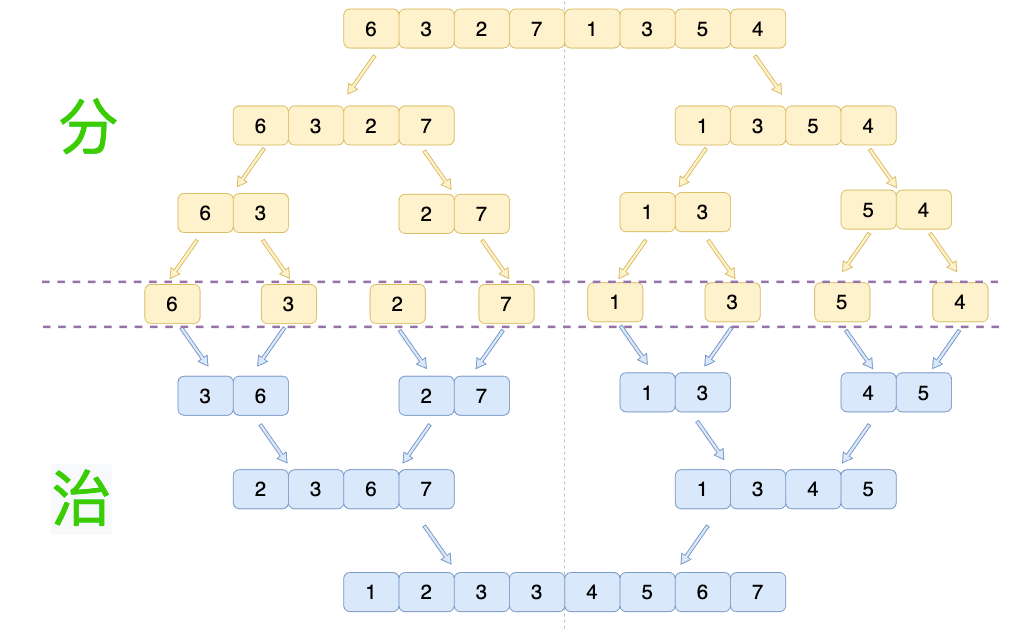
分阶段可以理解为就是递归拆分子序列的过程，递归的深度为log2n。而治的阶段则是将两个子序列进行排序的过程，我们通过图解看看治阶段最后一步中是如何将[2，3，6，7]和[1，3，4，5]这两个数组合并的。

图中左边是复制的临时数组，而右边是原数组，我们将左右指针对应的值进行大小比较，将较小的那个数放入原数组中，然后将相应的指针右移。比如第一步中，我们比较左边指针L指向的4和右指针R指向的1，R指向的1小，则把1放入原数组中的第一个位置中，然后R指针向右移动。后面再继续，直到左边临时数组的元素都按序覆盖了右边的原数组。最后我们通过上图再结合源码来看看吧：

class Solution {
    public int[] sortArray(int[] nums) {
        sort(0, nums.length - 1, nums);
        return nums;
    }

    // 分：递归二分
    private void sort(int l, int r, int[] nums) {
        if (l >= r) return;

        int mid = (l + r) / 2;
        sort(l, mid, nums);
        sort(mid + 1, r, nums);
        merge(l, mid, r, nums);
    }


    // 治：将nums[l...mid]和nums[mid+1...r]两部分进行归并
    private void merge(int l, int mid, int r, int[] nums) {
        int[] aux = Arrays.copyOfRange(nums, l, r + 1);

        int lp =l, rp = mid + 1;

        for (int i = lp; i <= r; i ++) {
            if (lp > mid) {                // 如果左半部分元素已经全部处理完毕
                nums[i] = aux[rp - l];
                rp ++;
            }  else if (rp > r) {          // 如果右半部分元素已经全部处理完毕
                nums[i] = aux[lp - l];
                lp ++;
            } else if (aux[lp-l] > aux[rp - l]) {     // 左半部分所指元素 > 右半部分所指元素
                nums[i] = aux[rp - l];
                rp ++;
            } else {                                  // 左半部分所指元素 <= 右半部分所指元素
                nums[i] = aux[lp - l];
                lp ++;
            }
        }
    }
}

我们可以看到，分阶段的时间复杂度是logN，而合并阶段的时间复杂度是N，所以归并算法的时间复杂度是O(N*logN)，因为每次合并都需要对应范围内的数组，所以其空间复杂度是O(N);

2. 归并排序（迭代版）

上面的归并排序是通过递归二分的方法进行数组切分的，其实我们也可以通过迭代的方法来完成这步，看下图：

其因为数组，所以我们直接通过迭代从1开始合并，其中sz就是合并的长度，这种方法也可以称为自底向上的归并，其具体的代码如下

class Solution {
    public int[] sortArray(int[] nums) {
        int n = nums.length;
        // sz= 1,2,4,8 ... 排序
        for (int sz = 1; sz < n; sz *= 2) {
            // 对 arr[i...i+sz-1] 和 arr[i+sz...i+2*sz-1] 进行归并
            for (int i = 0; i < n - sz; i += 2*sz ) {
                merge(i, i + sz - 1, Math.min(i+sz+sz-1, n-1), nums);
            }
        }
        return nums;
    }

   // 和递归版一样
    private void merge(int l, int mid, int r, int[] nums) {
        int[] aux = Arrays.copyOfRange(nums, l, r + 1);

        int lp =l, rp = mid + 1;

        for (int i = lp; i <= r; i ++) {
            if (lp > mid) {
                nums[i] = aux[rp - l];
                rp ++;
            }  else if (rp > r) {
                nums[i] = aux[lp - l];
                lp ++;
            } else if (aux[lp-l] > aux[rp - l]) {
                nums[i] = aux[rp - l];
                rp ++;
            } else {
                nums[i] = aux[lp - l];
                lp ++;
            }
        }
    }
}

3. 总结

好了，归并算法就介绍完了，再来总结一下：

归并排序是一种十分高效的排序算法，其时间复杂度为O(N*logN)。归并排序的最好，最坏的平均时间复杂度均为O(nlogn)，排序后相等的元素的顺序不会改变，所以也是一种稳定的排序算法。归并排序被应用在许多地方，其java中Arrays.sort()采用了一种名为TimSort的排序算法，其就是归并排序的优化版本。