5管运放/电流镜中的镜像零点分析

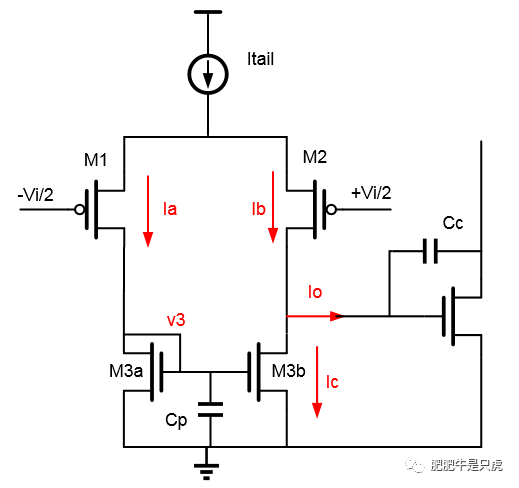
单端输出的5管运放或者电流镜存在一对高频零极点对，本文试图从多个角度推导、理解这个零点。

• 小信号图方法

先考虑低频情况，即不考虑寄生电容Cp

Ia = Ic = gm1*Vi/2

Ib = -gm1*Vi/2

输出电流Io = Ib-Ic = -gm1*Vi

再考虑一般情况，即考虑寄生电容Cp的影响

v3所在点的等效阻抗为 1/gm3和Cp的并联，Zeq=1/gm3*1/(1+sCp/gm3)

Ia = gm1*Vi/2

V3 = Ia Zeq = Vi/2 (gm1/gm3)*1/(1+sCp/gm3)

M3b的电流 Ic = V3gm3=Vi/2gm1/(1+sCp/gm3)

Ib = -gm1*Vi/2

输出电流 Io = Ib-Ic = -Vi/2 gm1 [1 + 1/(1+sCp/gm3)]

上式通分得到 Io = -Vi/2gm1 num/den

其中num = 2 + s*Cp/gm3

den = 1+ s*Cp/gm3

令num = 0，得到零点 z=-2*gm3/Cp

令den = 0，得到极点 p=-gm3/Cp

结论：

镜像电流镜处存在一对左半平面的零极点对，零点为极点的2倍

z = - 2*gm3/Cp

p=-gm3/Cp

1. 零极点的物理意义

极点：

由电阻1/gm3和Cp组成的RC并联网络在电流的驱动下形成极点频率。

零点：

当频率足够高时，Cp的阻抗足够低，流过Cp的电流足够大，改变通过M3a和M3b的电流的极性。

在零点频率处，流过各个器件的电流及其方向见下图。

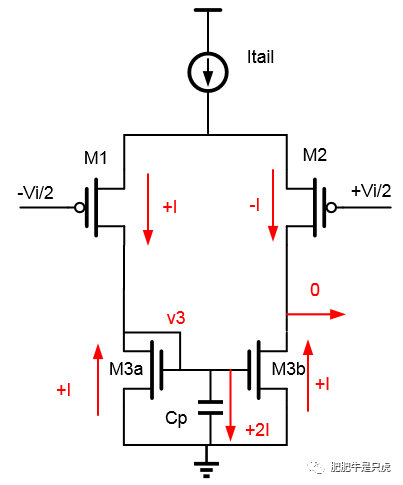
1. 更抽象的理解方式

大家应该听过类似的表达，“信号通过两条不同的路径到达同一个目的地，会形成零点。”我们试图将这个说法抽象化、模型化，并证明其合理性。

假设信号通过两条不同的路径（分别为路径A、路径B）到达目的地，两条路径的传函分别为：

A通路：A1(s) = A1/(1-s/p1)

B通路：A2(s) = A2/(1-s/p2)

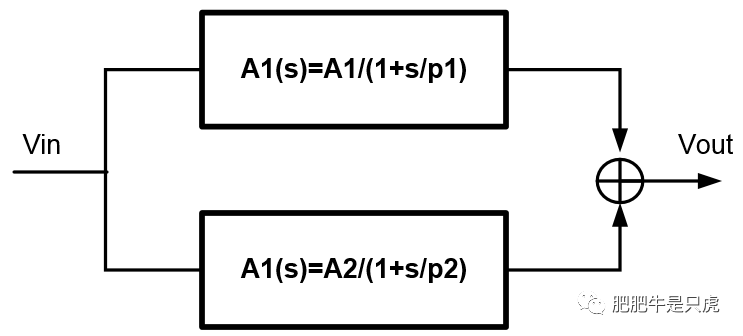
Vout/Vin = A1/(1-s/p1) + A2/(1-s/p2)

对上式进行通分化简

Vout/Vin = （A1+A2）*num/den

其中num = 1 - s/(A1+A2)*(A1/p2+A2/p2)

den  = (1-s/p1)(1-s/p2)

令num=0，得到零点 z = (A1+A2)/(A1/p2+A2/p1)

令den=0，得到极点 p1、p2

具体到镜像电流镜应用 ，也是两条通路，

快通路：从M2直接到输出，传函 I1(s) = I/(1-s/p1)，其中p1为输出极点

慢通路：从M1-->M3a-->M3b-->输出，

慢通路传函：I2(s) = -I/(1-s/p1)/(1-s/p2)，其中p2为镜像极点

总的传函：Io(s) = I1(s) - I2(s) = I*(2-s/p2)/[(1-s/p1)(1-s/p2)]

很显然，零点 z=2*p2
至此，我们通过这种抽象建模，也证明了镜像零点的存在，且推导了其精确表达式。