

信号处理电路-移相电路设计
电子说
描述
移相电路是一种特殊的信号处理电路,改变输出信号相对与输入信号的相位(时延),不改变信号的幅度。移相电路在实际工程中应用广泛,如锁定放大器、外差接收、同步、波形合成等。
移相电路的本质是改变输出信号与输入信号的相位关系,所以必须会用到电容器,其实移相电路也可称为全通滤波器。
在多数情况下,滤波器的幅度响应是首要考虑因素。不影响信号幅度但会导致相移的另一类滤波器称为全通滤波器。该滤波器的目的是给电路的响应增加相移(延迟)。全通滤波器的幅度在所有频率下一致。
然而,在频率从0扫频至无穷大时,相位响应会从0°变化至360°(双极点滤波器)。全通滤波器的一种用途是提供相位均衡,一般用在脉冲电路中。同时也可用在单边带、抑制载波 (SSB-SC)调制电路中。
全通滤波器的传递函数为:
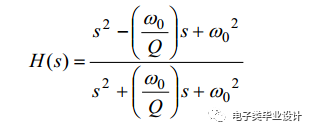
全通传递函数可以合成为:
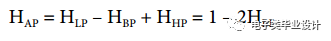
一阶全通
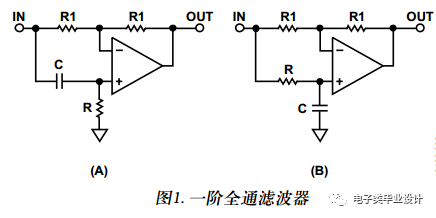
一阶全通滤波器的一般形态如图 1所示。如果其功能为简单的RC高(图1A),则电路的相移范围为−180°(0 Hz)至0°(高频)。当 ω = 1/RC时,为−90°。可将电阻设为可变,以便在具体频率下进行延迟调节。
如果将功能改成低通功能(图1B),则滤波器仍然为一阶全通,延迟等式仍然有效,但信号会反相,变化范围为0°(直流)至−180°(高频)。
二阶全通
图2所示二阶全通电路首次由 Delyiannis描述。这种电路的最大魅力在于只需要一个运算放大器。同时记住,全通滤波器也可实现为1 – 2 BP。
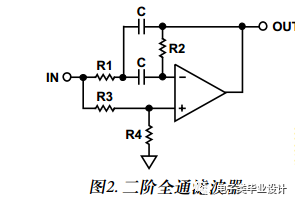
我们可以利用本文中讨论的带通实现方式来构建该滤波器,但一定要知道, BP是否会使相位反转。另外需要记住BP部分的增益必须为2。为此,双放大器带通滤波器(DABP)结构十分有用,因为其增益固定为2。
- 在选择运算放大器时,我们主要考虑带宽问题。根据经验,放大器在谐振频率下的开环增益不得低于20 dB。同时,由于反馈网络中有一个电容,所以,可能不大适合使用电流反馈放大器。
图3和图4总结了多种有源滤波器实现方式的设计方程式。在所有情况下, H、 ωo、 Q和α都是已知的,取自设计表。
一阶全通设计方程
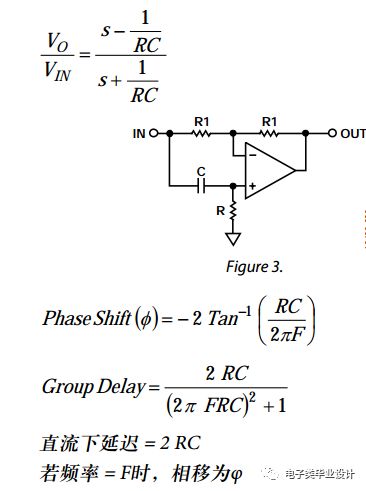

二阶全通设计方程
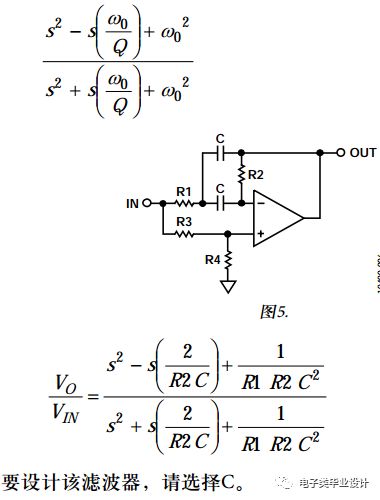

-
如何利用模拟电路对方波信号进行移相?2024-09-11 972
-
rc电路移相特性的观察与分析2024-03-09 4912
-
精确移相电路的设计举例(1)2023-10-13 4919
-
使用移相电路计算相位的方式2022-01-11 5853
-
阻容移相桥触发电路是如何实现移相的2021-08-19 3825
-
求一种采用数字控制的三相移相触发电路设计方案?2021-04-08 1749
-
如何使用移相电路计算相位2021-01-23 20023
-
移相电路设计 RC移相电路示意图2020-11-16 64017
-
浅谈0-180度移相电路设计案例2020-07-21 19826
-
PWM再生成电路的组成与高精度脉宽调制信号移相电路的设计2017-11-06 1282
-
请问移相电路如何设计?2017-03-18 10878
-
信号处理电路设计介绍2016-05-04 604
-
移相电路的设计2014-03-15 2914
-
相控变流器的垂直移相电路2010-04-26 606
全部0条评论

快来发表一下你的评论吧 !

