

输入电容和负载电容引起的放大器振荡问题
电子说
描述
输入电容和负载电容引起的放大器振荡问题
学过模拟电路的人可能都遇见过:各个电路模块原先不振荡,把所有电路模块连起来(接上负载),电路振荡了!这是什么原因,如何避免?其中有相当一部分的原因就是输入电容和负载电容引起的放大器振荡,这次推文我们来研究一下这个问题:如何在实际闭环系统中测量相位裕量和增益裕量,如何根据闭环系统的幅频特性判断相位裕量,如何根据脉冲响应过冲判断相位裕量,如何快速补偿相位裕量....
一、实际闭环系统中测量相位裕量和相位零点补偿
1)振荡分析经典教科书里都是分析环路增益AF,得到两个指标:增益裕量和相位裕量;增益裕量就是负反馈时,AF的相位为180度,刚好变正反馈时,|AF|与0db的差值;相位裕量就是|AF|为0db时,AF的相位与180度(或-180度)的差值,这是衡量放大器稳定度的指标,一般相位裕量在45度到60度时可以认为比较稳定,大于60度当然更稳定,但是这在实际放大器中不多见,一般相位裕量在30度以下,即使在实验室不振荡稳定工作,也可能由于环境、负载等因素变化而今后振荡,即便没有振荡,这种放大器的阶跃或脉冲响应会存在很大的衰减振荡,也会影响电路使用,所以一般相位裕量小于45度到30度时,设计人员都应该考虑避免自激振荡或衰减振荡的措施。
那么在闭环放大器结构中如何测量AF的相位裕量和增益裕量?这里我们用反向放大器的仿真演示来代替实验操作,其它放大器的测试原理是一样的:
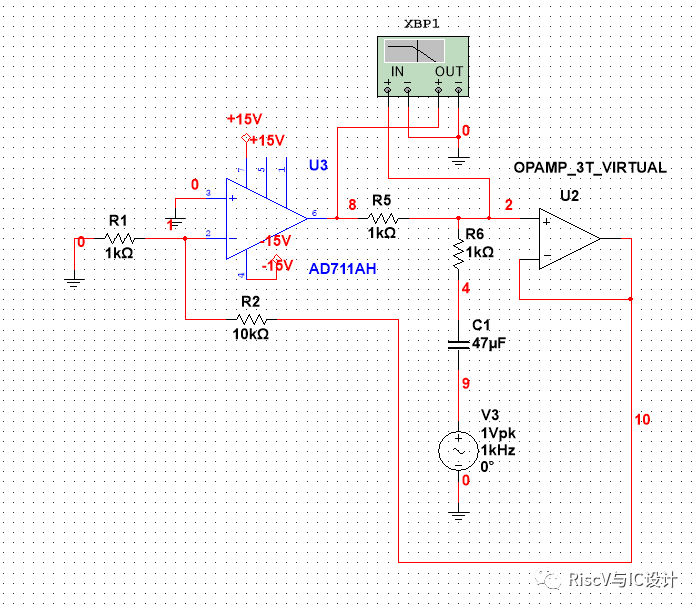
测试结果:
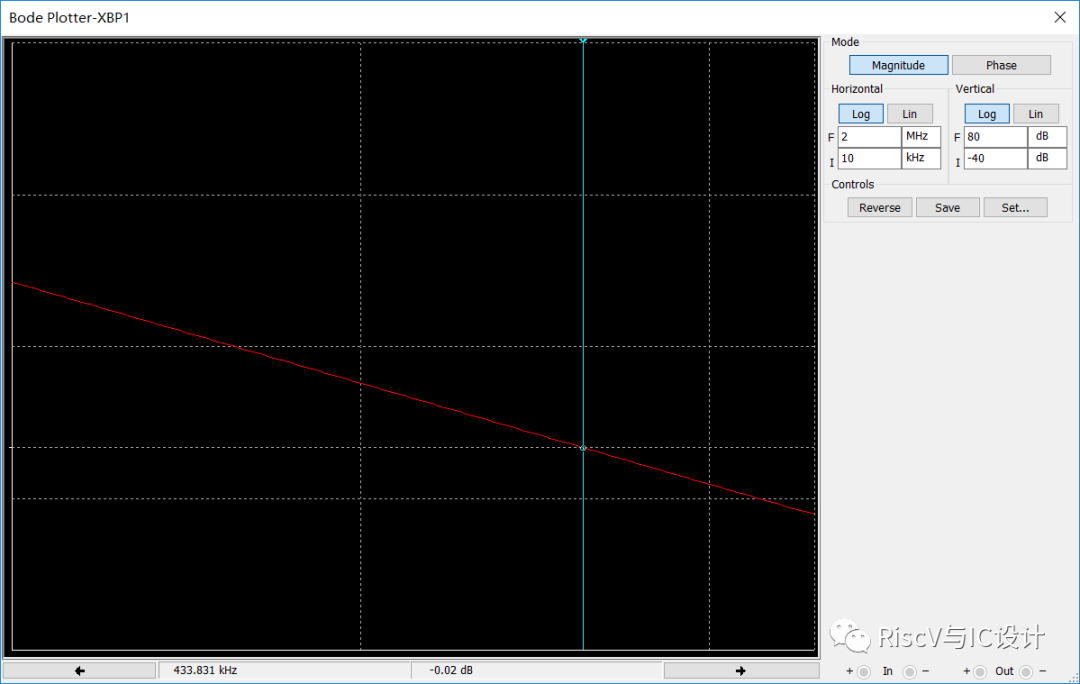
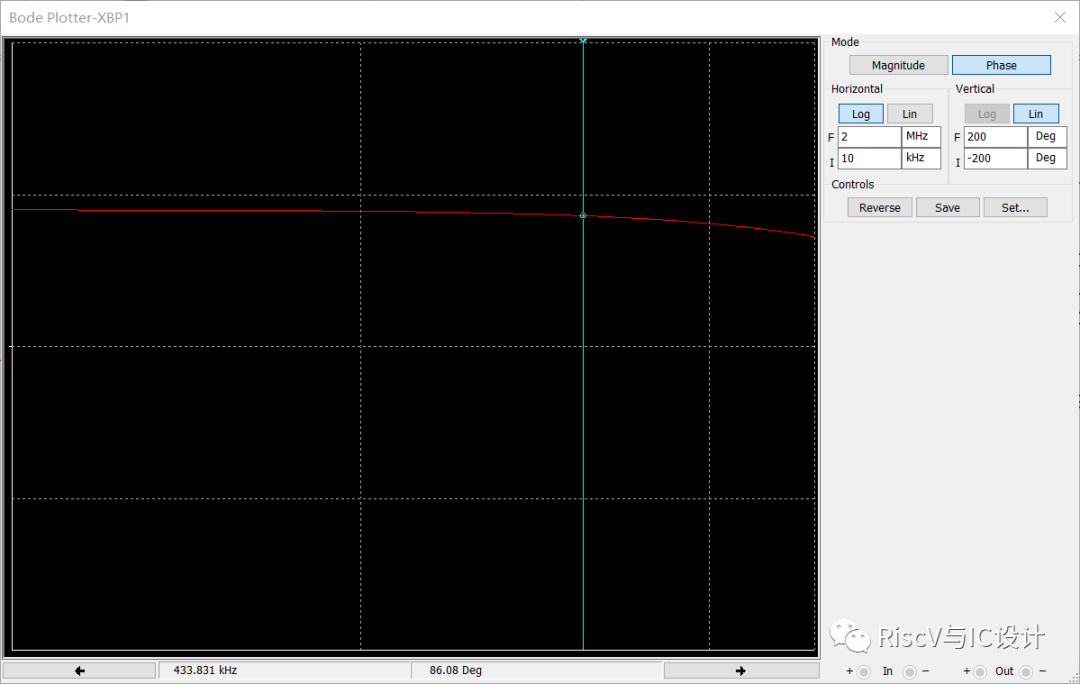
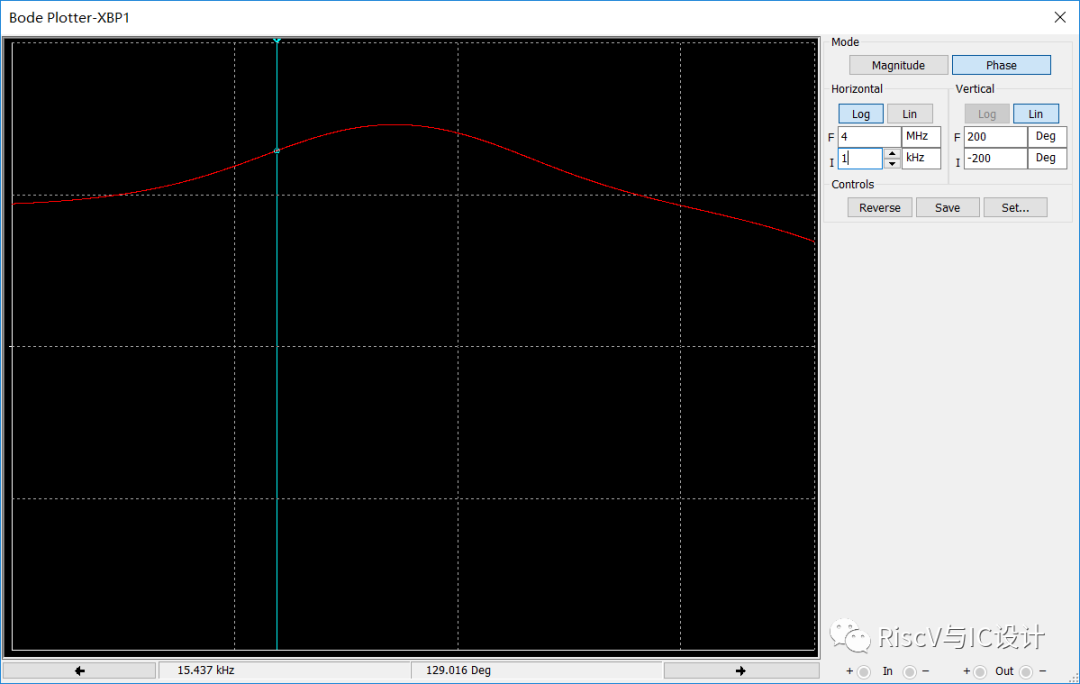
可见上图的相位裕量为86.08度
实际放大器由于各种原因,可能在运放输入端或负载端引入分布电容,比如运放输出驱动一个电缆时,电缆的等效电容就比较大,以下对此做仿真探讨:
下图是在原图的输入端并联了一个1nF的小电容
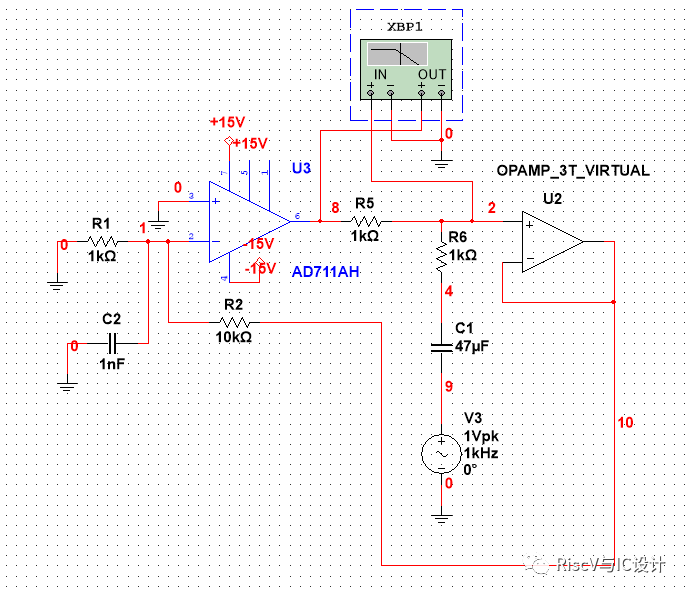
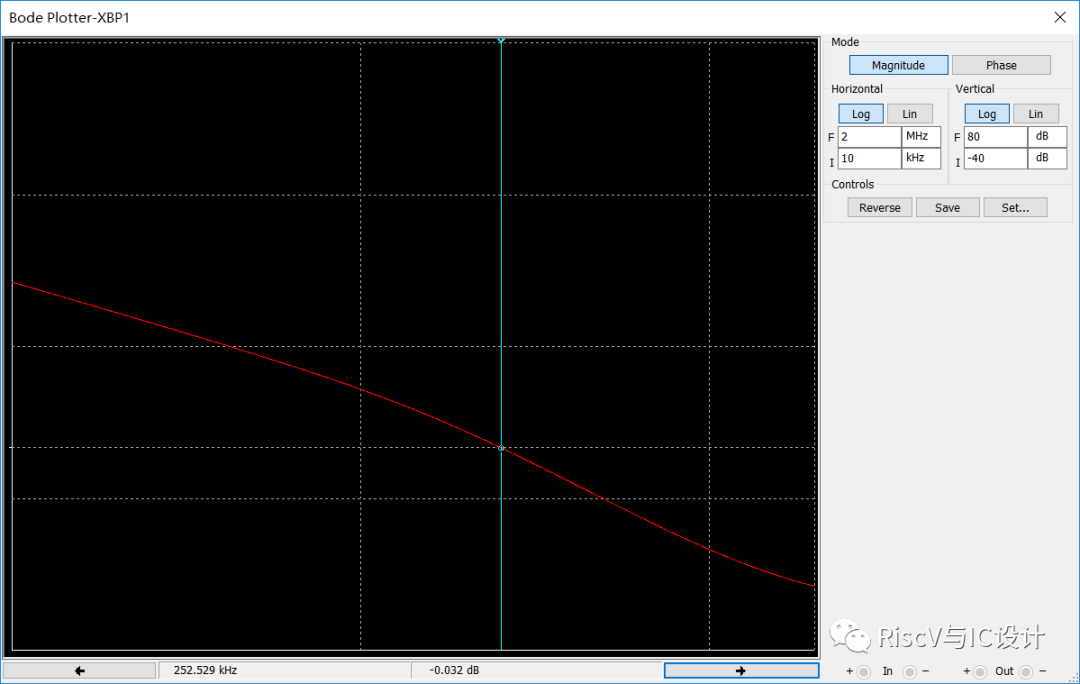
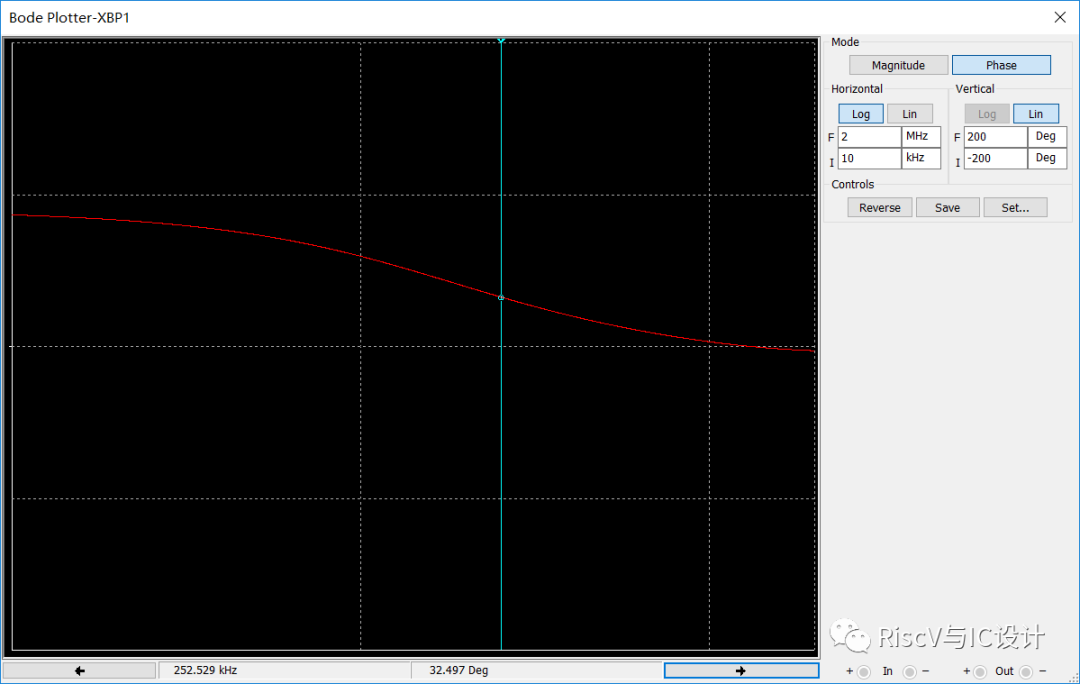
此时放大器的相位裕量已经下降为32.497度!现在加一个1khz 0.5v的方波,其时域输出信号已存在过冲和衰减振荡,如下图所示:
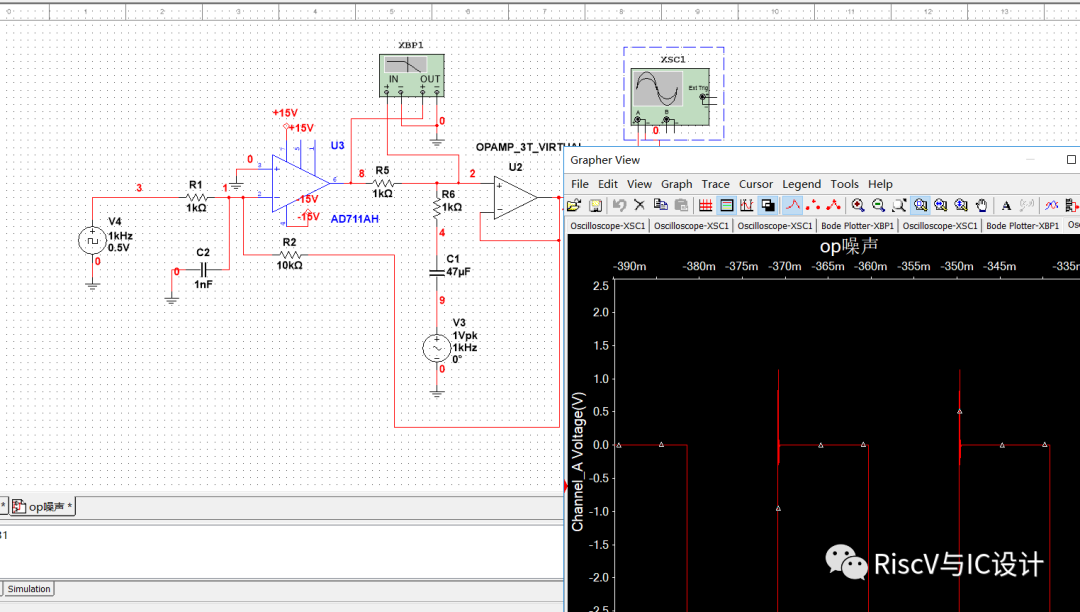
如果我们再在输出端加一个10nf负载电容,则时域波形的过冲振荡更加明显:
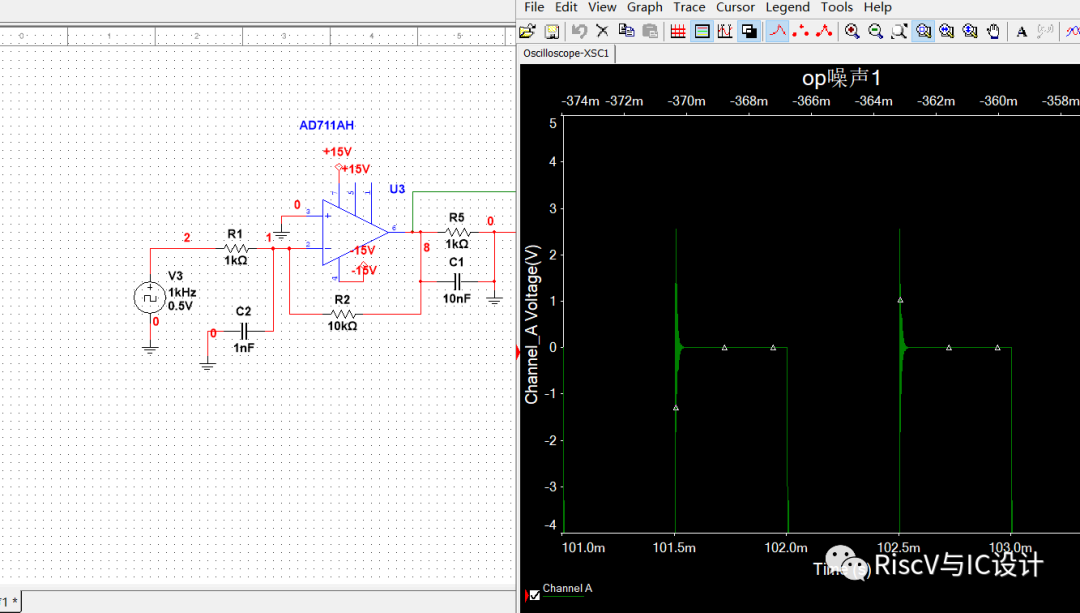
如果我们再把输出端电容加大到100nf:
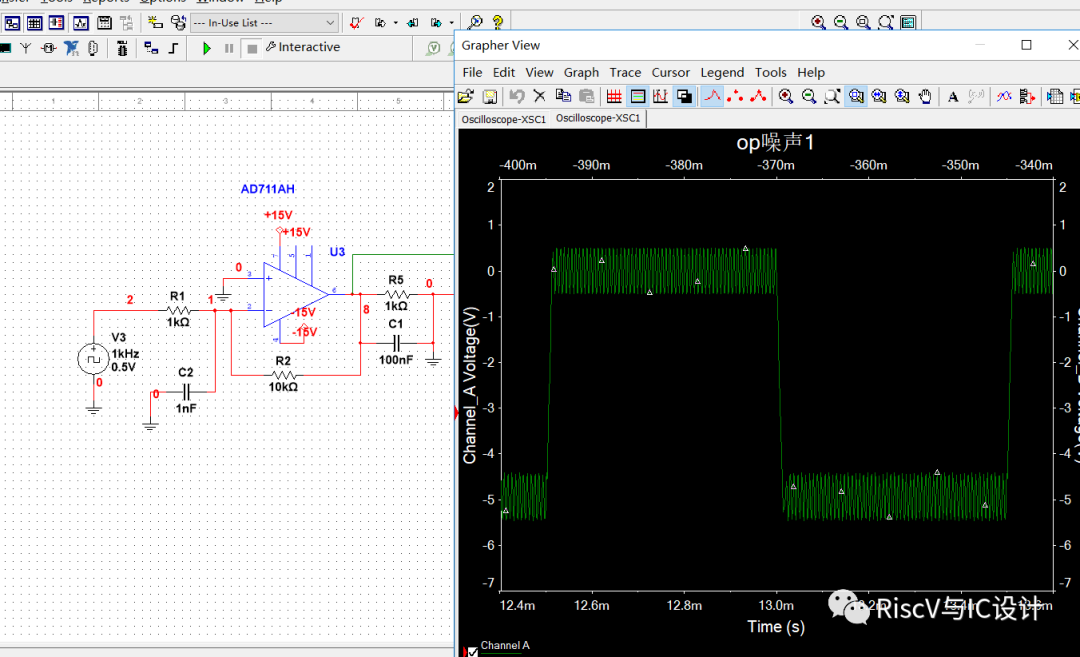
可见输入/输出端端引入的分布电容,是会降低相位裕量,引起衰减振荡甚至自激的!
解决的办法就是相位补偿,相位补偿有以下三种:
- 超前补偿 2)滞后补偿 3) 超前-滞后补偿
其中2)和3)方法需要足够大的相移补偿,计算复杂,这里只介绍简单的超前补偿。
先看补偿电路与补偿效果:
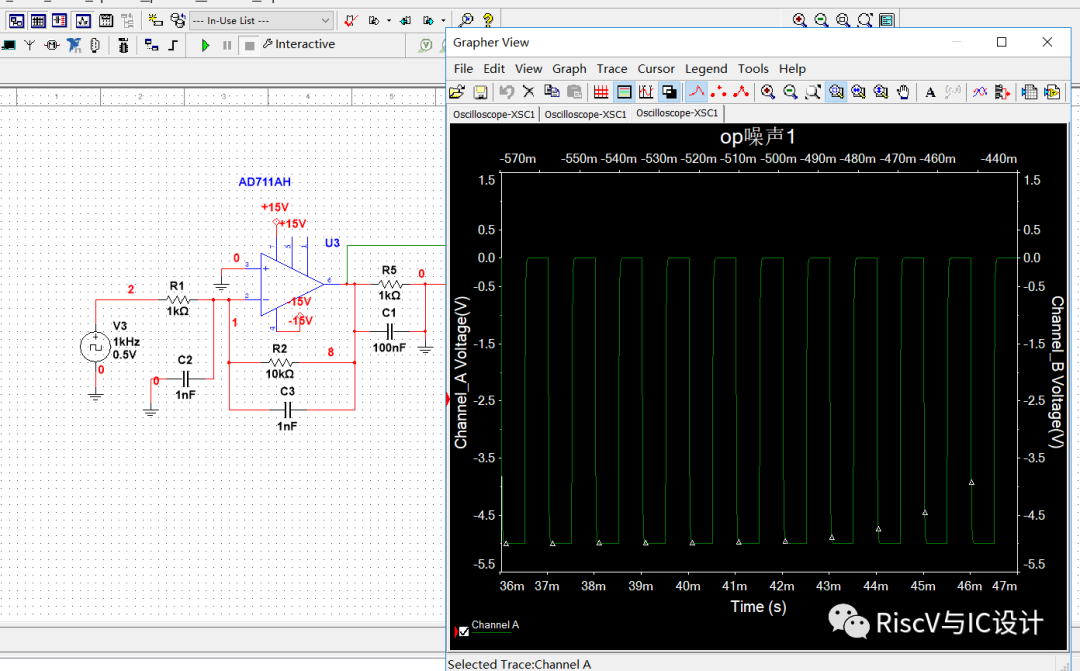
与前图相比,我们在反馈电阻R2两端并接了一个小电容C3,其时域脉冲响应波形已无衰减振荡!
此补偿电容C3为什么有相位补偿效果?因为它引入了一个零点,零点的频率为fz=1/(2PIR2*C3),在传输函数的零点频率处会相位超前45度,此零点的相位补偿可以提示相位裕量。
有点遗憾的是此电路还同时提供了一个新极点,极点频率为fm=(1+R2/R1)*fz,增益越大,新引入的极点频率越高,不利的影响越小,补偿效果越好,所以增益越高补偿越容易!
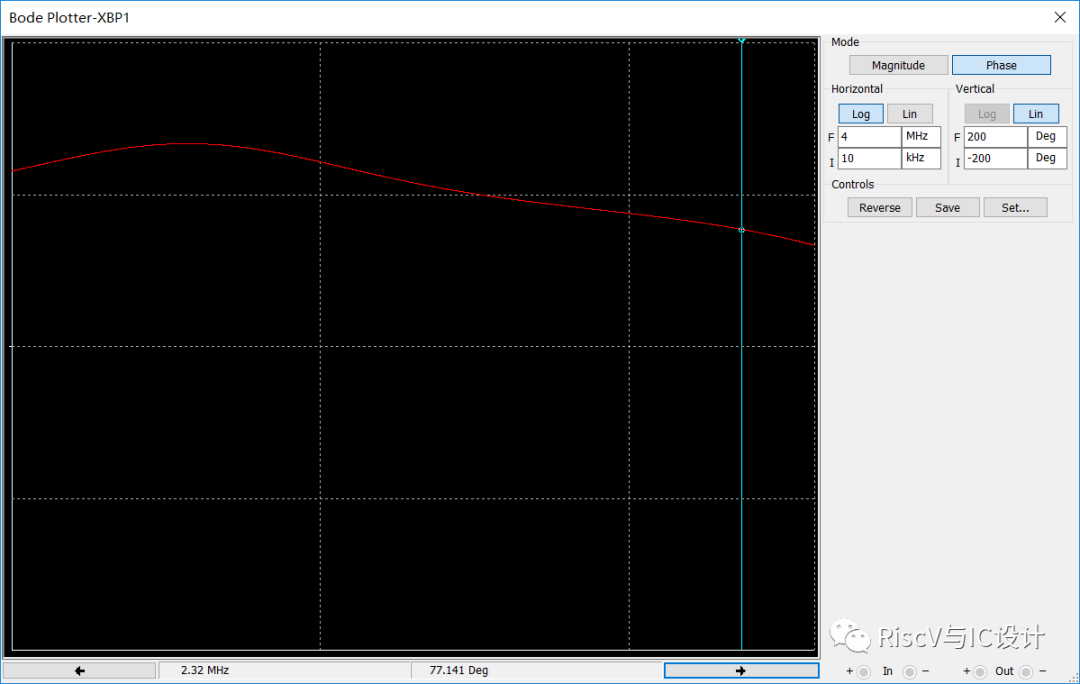
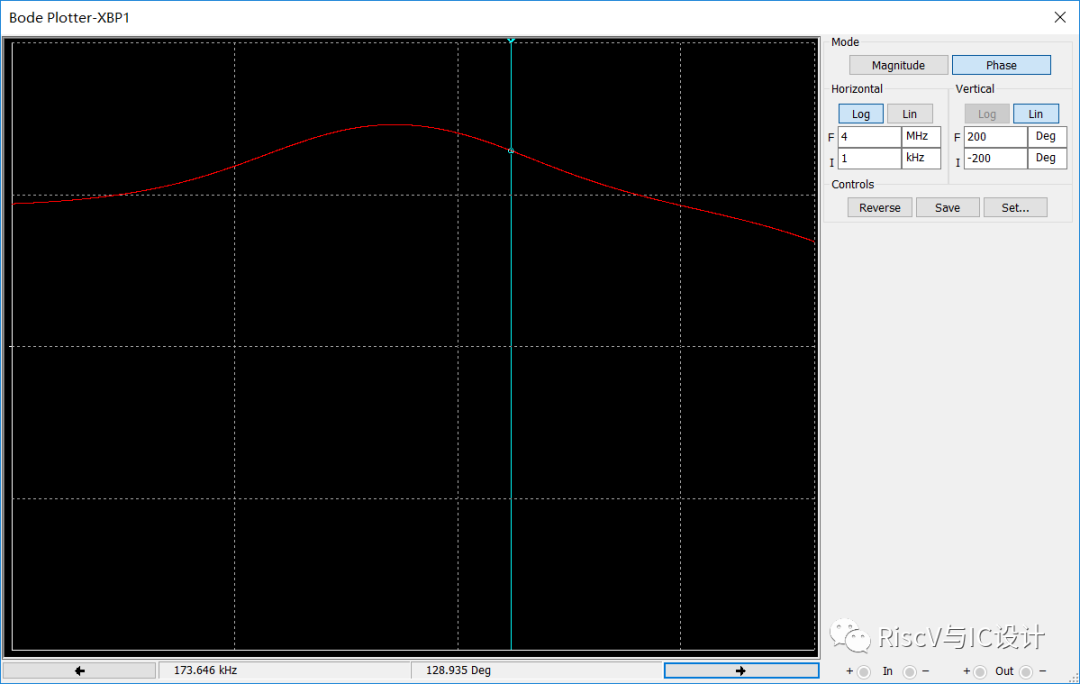
上图是补偿后的相位仿真测试,相位裕量为77.141度,在图左边相位明显出现了一个突起尖峰,尖峰的一半位置对应的频率为15.4khz左右和173kHz左右,由于是手工目测不是太准确,根据fz=1/(2PIR2*C3)可以求出补偿引入的零点频率为15.9khz,而引入的极点频率为fm=(1+R2/R1)*fz=175khz,可见相当准确!
可能有人会问为啥你测量峰值变化的一半位置?因为零极点都可以写成1+jw*RC,当频率w变化时引入的相位变化为0--90度,中间一半位置为45度,刚好对应零极点频率1/RC.
为啥补偿的同时会引入一个高频极点?下面简单推导:
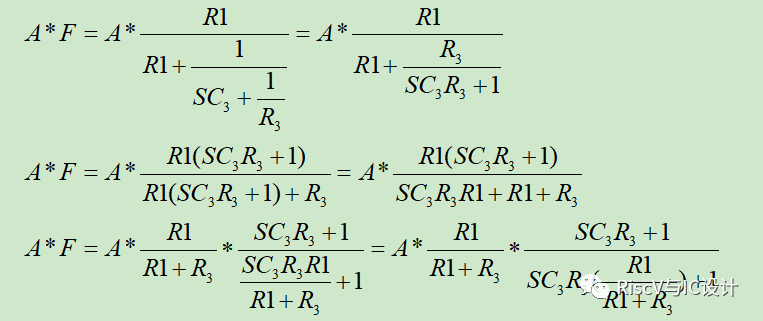
可见零点为1/(R3C3), 极点为(1+R3/R1)*(1/(R3C3))
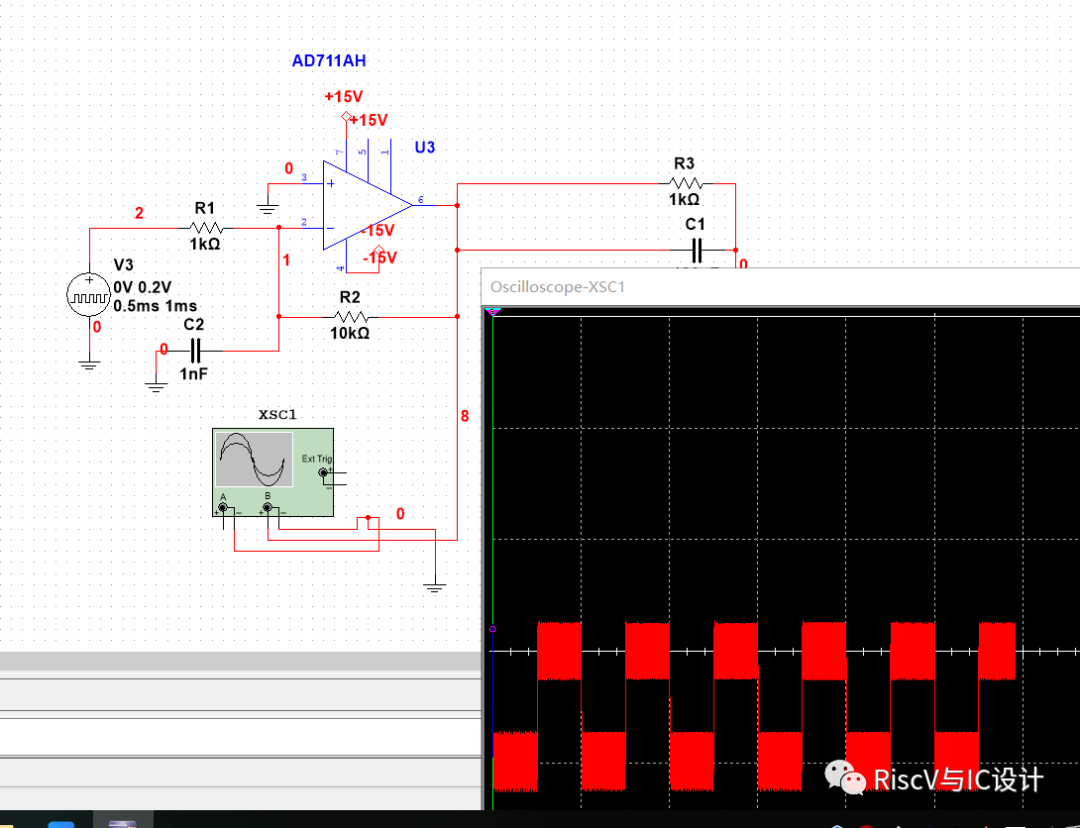
对于输出负载电容引起的振荡或衰减振荡,也可以不用C3电容补偿,而在输出端加以小电阻:
下图是补偿前,输出有明显振荡:
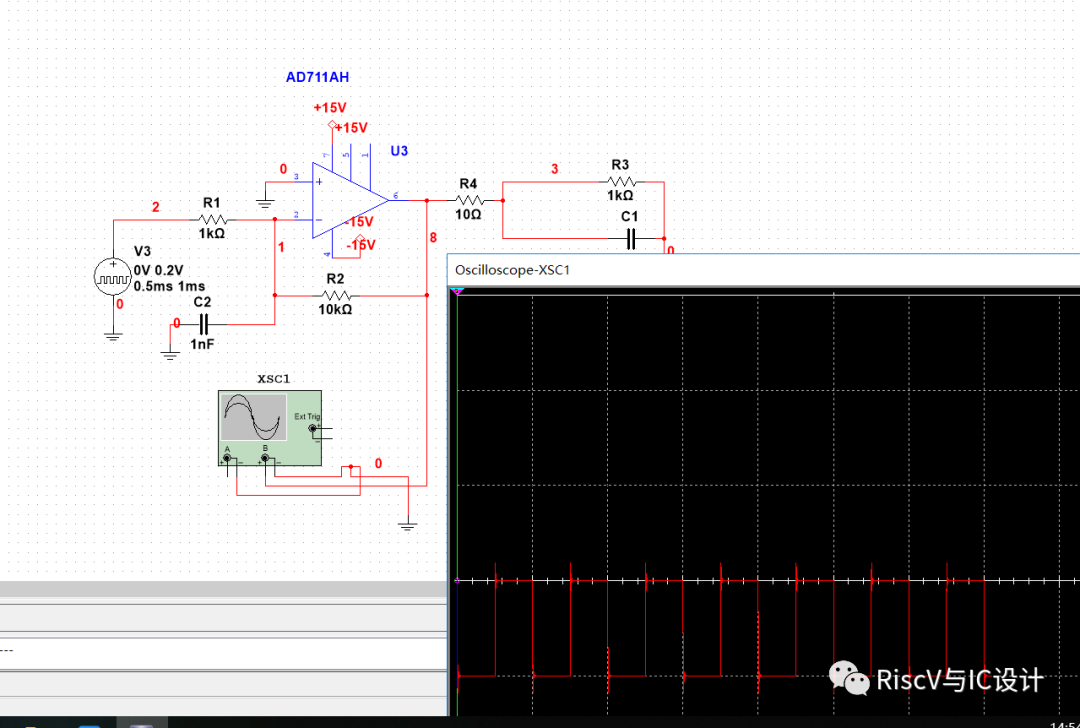
下图是输出小电阻补偿后,已无明显振荡,其原理还是减小相位滞后的原理:
相位裕量与闭环频率特性峰值的关系
除了上面介绍的传统测量实际放大器相位裕量方法,还可以分析闭环系统的幅频特性来估算相位裕量:

同理可以推导出其他相位裕量时的情况:
相位裕量 峰值/db
90度 0db
60度 0.2db
45度 2.4db
30度 5.8db
下面简单验证以下:
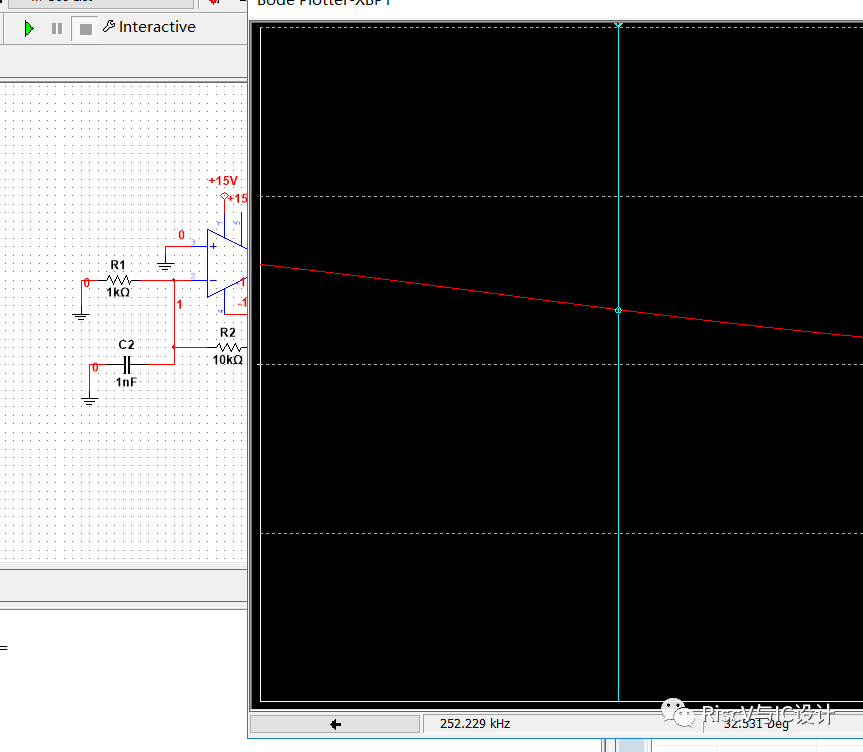
此电路相位裕量接近32.531度
做交流分析结果如下:
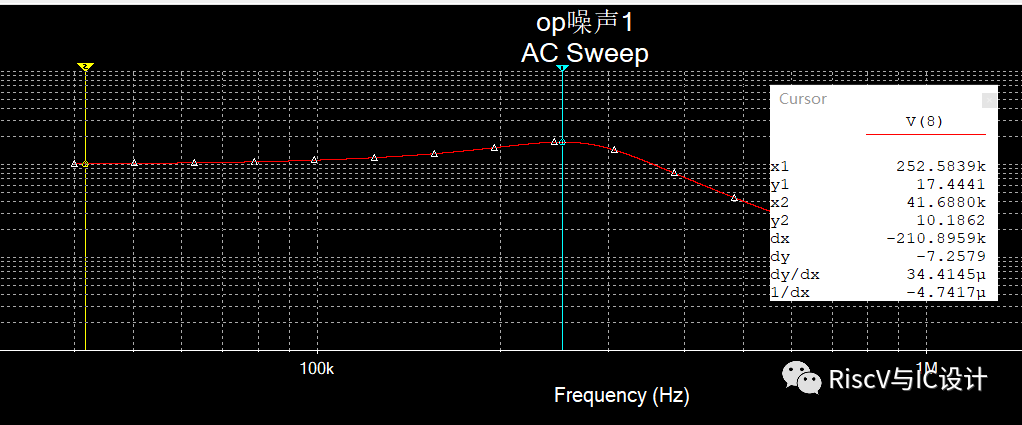
峰值为17.444, 低频为10.186, 比值为1.713=4.67db,
而
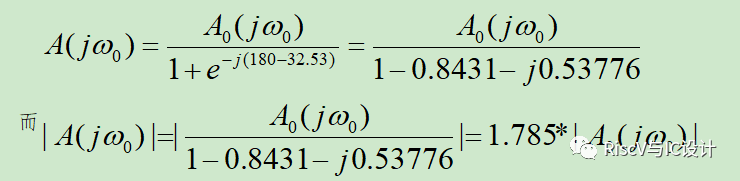
与1.713非常接近,在计算误差以内
可见如果一个闭环系统的幅频特性出现波峰,只要波峰小于低频时的1.3倍(2.4db),都可以认为系统是稳定的。
三、相位裕量与逸出量的关系
第一/二种方法都是比较准确的,但是有点麻烦,第二种需要用幅频特性测试仪扫描幅频特性,这里介绍的第三种方法最简单,但当系统的极点较多时就不准确了。
第三种方法是根据闭环系统在时域上的脉冲响应波形的过冲(逸出量)来估算相位裕量:
关系基本同二:
相位裕量 逸出量/db
90度 0db
60度 0.2db
45度 2.4db
30度 5.8db
比如前图,相位裕量32.5度:
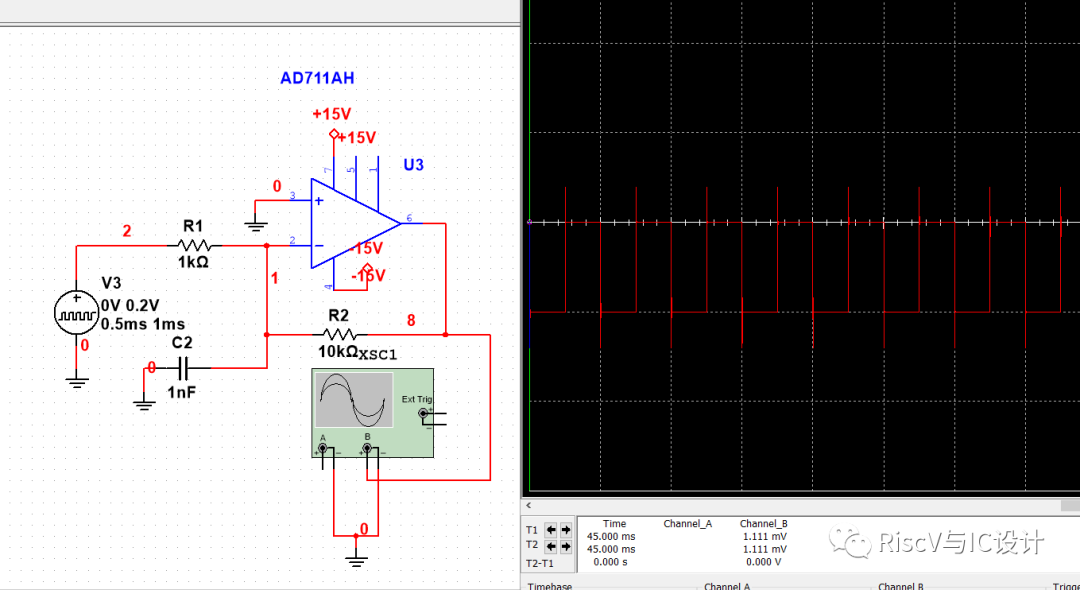
上升沿逸出量为0.7875596V
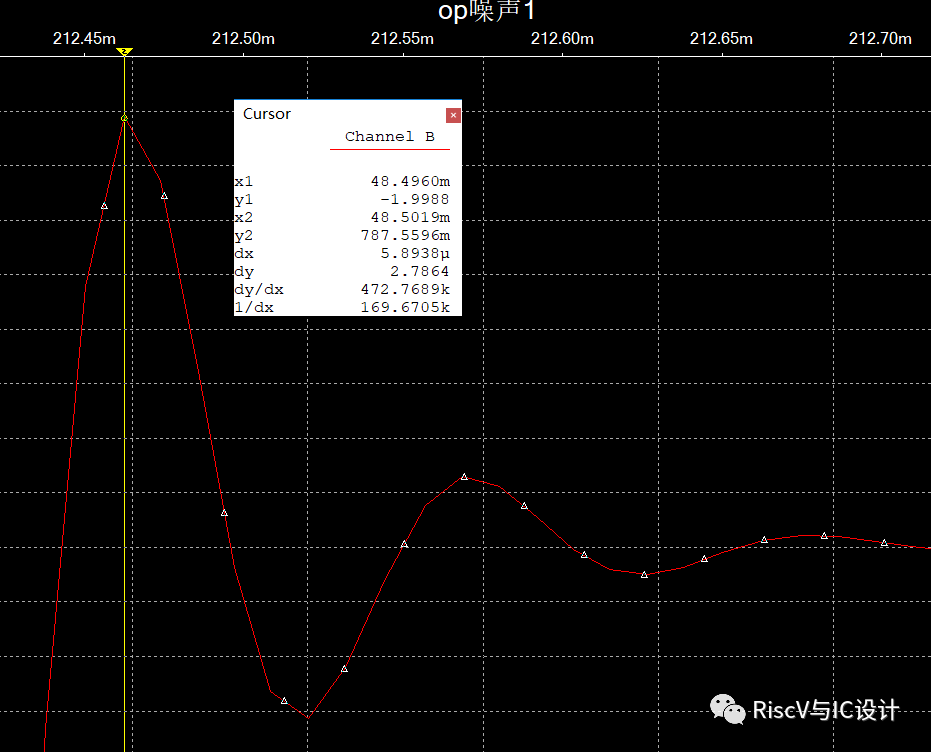
下升沿逸出量为-2.7919V
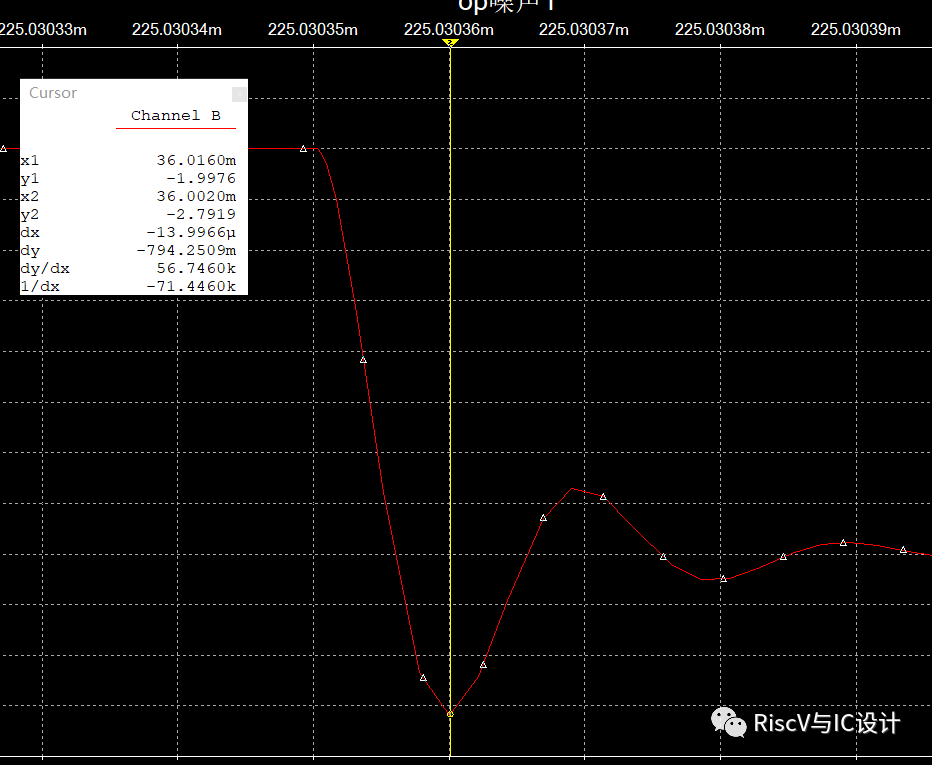
总逸出量为0.7876-(-2.7919)=3.5795,而稳态输出为2,则比值为1.79,与前述计算、测量基本一致。
-
请问运算放大器如何驱动电容负载?2024-09-12 470
-
电容性负载和相位裕度2018-10-25 3190
-
运算放大器振荡的原因是啥?2018-10-31 3487
-
什么是输出引脚补偿?驱动电容负载时怎么防止意外高频振荡?2021-04-07 1184
-
运算放大器稳定性和输入电容2009-08-08 509
-
电容性负载和相位裕度技术详解2017-09-18 1156
-
直接测量运算放大器输入差分电容的方法详细说明2021-01-12 1419
-
DN429 - 纤巧型放大器可快速驱动重电容性负载2021-03-20 761
-
引起放大器振荡的原因是什么,如何解决?2021-05-01 20416
-
振荡运算放大器电容性负载稳定性2021-11-19 1893
-
测量运算放大器的输入电容2023-01-29 4023
-
电压放大器如何驱动电容性负载的2023-07-12 1143
-
电容反馈的闭环放大器,与电容并联的电阻是什么作用?2023-09-17 3325
-
在测量运算放大器输入电容时,应关注哪些方面?2023-10-25 1112
-
耦合电容的大小影响放大器的哪些性能2024-08-07 2920
全部0条评论

快来发表一下你的评论吧 !

