使用Pytorch实现频谱归一化生成对抗网络(SN-GAN)

自从扩散模型发布以来，GAN的关注度和论文是越来越少了，但是它们里面的一些思路还是值得我们了解和学习。所以本文我们来使用Pytorch 来实现SN-GAN

谱归一化生成对抗网络是一种生成对抗网络，它使用谱归一化技术来稳定鉴别器的训练。谱归一化是一种权值归一化技术，它约束了鉴别器中每一层的谱范数。这有助于防止鉴别器变得过于强大，从而导致不稳定和糟糕的结果。

SN-GAN由Miyato等人(2018)在论文“生成对抗网络的谱归一化”中提出，作者证明了sn - gan在各种图像生成任务上比其他gan具有更好的性能。

SN-GAN的训练方式与其他gan相同。生成器网络学习生成与真实图像无法区分的图像，而鉴别器网络学习区分真实图像和生成图像。这两个网络以竞争的方式进行训练，它们最终达到一个点，即生成器能够产生逼真的图像，从而欺骗鉴别器。

以下是SN-GAN相对于其他gan的优势总结:

• 更稳定，更容易训练
• 可以生成更高质量的图像
• 更通用，可以用来生成更广泛的内容。

模式崩溃

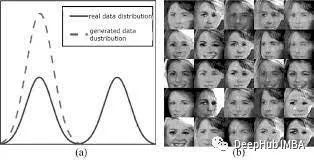
模式崩溃是生成对抗网络(GANs)训练中常见的问题。当GAN的生成器网络无法产生多样化的输出，而是陷入特定的模式时，就会发生模式崩溃。这会导致生成的输出出现重复，缺乏多样性和细节，有时甚至与训练数据完全无关。

GAN中发生模式崩溃有几个原因。一个原因是生成器网络可能对训练数据过拟合。如果训练数据不够多样化，或者生成器网络太复杂，就会发生这种情况。另一个原因是生成器网络可能陷入损失函数的局部最小值。如果学习率太高，或者损失函数定义不明确，就会发生这种情况。

以前有许多技术可以用来防止模式崩溃。比如使用更多样化的训练数据集。或者使用正则化技术，例如dropout或批处理归一化，使用合适的学习率和损失函数也很重要。

Wassersteian损失

Wasserstein损失，也称为Earth Mover’s Distance(EMD)或Wasserstein GAN (WGAN)损失，是一种用于生成对抗网络(GAN)的损失函数。引入它是为了解决与传统GAN损失函数相关的一些问题，例如Jensen-Shannon散度和Kullback-Leibler散度。

Wasserstein损失测量真实数据和生成数据的概率分布之间的差异，同时确保它具有一定的数学性质。他的思想是最小化这两个分布之间的Wassersteian距离(也称为地球移动者距离)。Wasserstein距离可以被认为是将一个分布转换为另一个分布所需的最小“成本”，其中“成本”被定义为将概率质量从一个位置移动到另一个位置所需的“工作量”。

Wasserstein损失的数学定义如下:

对于生成器G和鉴别器D, Wasserstein损失(Wasserstein距离)可以表示为:

Jensen-Shannon散度(JSD): Jensen-Shannon散度是一种对称度量，用于量化两个概率分布之间的差异

对于概率分布P和Q, JSD定义如下:

JSD(P∥Q)=1/2(KL(P∥M)+KL(Q∥M))

M为平均分布，KL为Kullback-Leibler散度，P∥Q为分布P与分布Q之间的JSD。

JSD总是非负的，在0和1之间有界，并且对称(JSD(P|Q) = JSD(Q|P))。它可以被解释为KL散度的“平滑”版本。

Kullback-Leibler散度(KL散度):Kullback-Leibler散度，通常被称为KL散度或相对熵，通过量化“额外信息”来测量两个概率分布之间的差异，这些“额外信息”需要使用另一个分布作为参考来编码一个分布。

对于两个概率分布P和Q，从Q到P的KL散度定义为:KL(P∥Q)=∑x P(x)log(Q(x)/P(x))。KL散度是非负非对称的，即KL(P∥Q)≠KL(Q∥P)。当且仅当P和Q相等时它为零。KL散度是无界的，可以用来衡量分布之间的不相似性。

1-Lipschitz Contiunity

1- lipschitz函数是斜率的绝对值以1为界的函数。这意味着对于任意两个输入x和y，函数输出之间的差不超过输入之间的差。

数学上函数f是1-Lipschitz，如果对于f定义域内的所有x和y，以下不等式成立:

|f(x) — f(y)| <= |x — y|

在生成对抗网络(GANs)中强制Lipschitz连续性是一种用于稳定训练和防止与传统GANs相关的一些问题的技术，例如模式崩溃和训练不稳定。在GAN中实现Lipschitz连续性的主要方法是通过使用Lipschitz约束或正则化，一种常用的方法是Wasserstein GAN (WGAN)。

在标准gan中，鉴别器(也称为WGAN中的批评家)被训练来区分真实和虚假数据。为了加强Lipschitz连续性，WGAN增加了一个约束，即鉴别器函数应该是Lipschitz连续的，这意味着函数的梯度不应该增长得太大。在数学上，它被限制为:

∥∣D(x)−D(y)∣≤K⋅∥x−y∥

其中D(x)是评论家对数据点x的输出，D(y)是y的输出，K是Lipschitz 常数。

WGAN的权重裁剪:在原始的WGAN中，通过在每个训练步骤后将鉴别器网络的权重裁剪到一个小范围(例如，[-0.01,0.01])来强制执行该约束。权重裁剪确保了鉴别器的梯度保持在一定范围内，并加强了利普希茨连续性。

WGAN的梯度惩罚: WGAN的一种变体，称为WGAN-GP，它使用梯度惩罚而不是权值裁剪来强制Lipschitz约束。WGAN-GP基于鉴别器的输出相对于真实和虚假数据之间的随机点的梯度，在损失函数中添加了一个惩罚项。这种惩罚鼓励了Lipschitz约束，而不需要权重裁剪。

谱范数

从符号上看矩阵