

LLC串联谐振拓扑谐振腔电压概述
电子说
描述
1.概述:
忽略高次谐波,假设变换器的功率传输,仅是电压和电流通过傅里叶展开的一次基波部分,被称为FHA 基波分析法。这也是谐振网络的选频特性,适合所有的谐振类拓扑。
2.LLC串联谐振拓扑谐振腔电压:
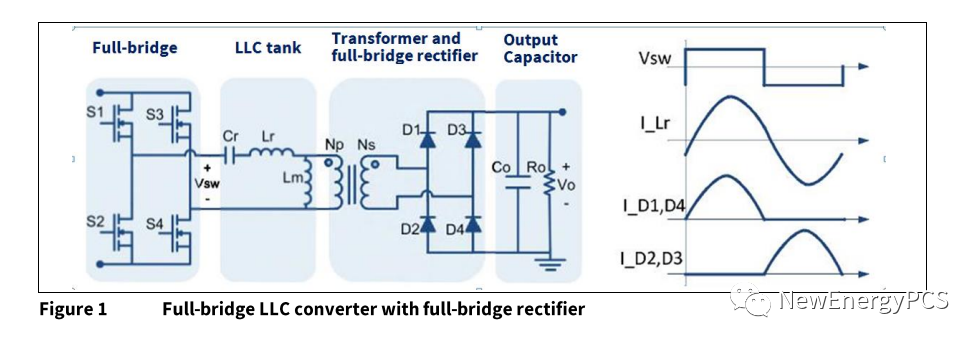
LLC串联谐振全桥
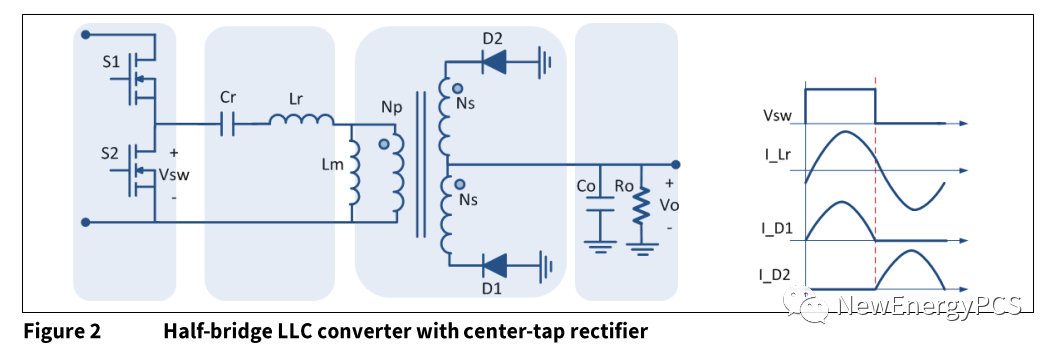
LLC串联谐振半桥
LLC全桥中点电压:
S1 S4 采用同一驱动信号,S2 S3采用同一驱动信号,占空比均为50%。S1S4 与 S2S3不直通存在死区。所以中点电压Vsw,形成幅值±Vin的方波电压,使用傅里叶展开中点电压波形。
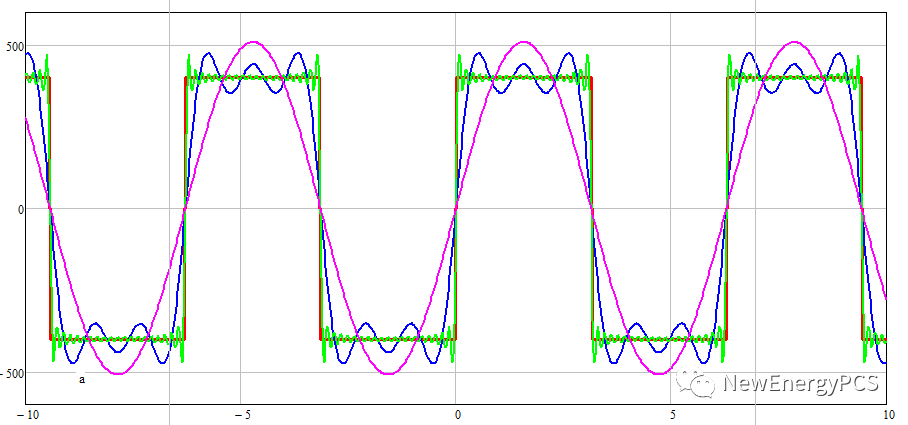
谐波取5次就很接近方波了,当取到39次就非常逼近了实际全桥中点电压。
单次谐波含量

单次谐波越高,幅值越小,频率越高。
LLC半桥中点电压:
S1 S2 是对称性半桥,每个开关管导通占空比50%(实际<50%),S1 S2不直通存在死区,所以S1 S2中点电压形成幅值为Vin,占空比50%的方波电压。使用傅里叶展开中点电压波形。

谐波取5次就很接近方波了,当取到39次就非常逼近了实际半桥中点电压。
单次谐波含量
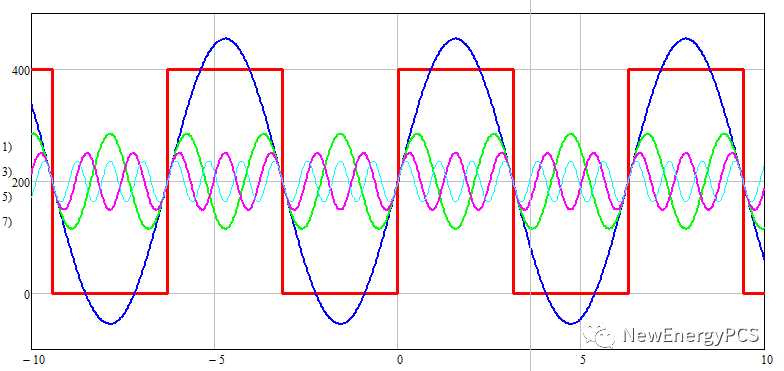
单次谐波越高,幅值越小,频率越高。
由于谐振电容Cr的存在有两个作用,一个是隔直作用,使变压器不容易饱和。一个是谐振电容。故输入到LLC的谐振网络没有直流分量。故计算中去掉直流分量。
FHA为了简化分析计算,只考虑基本起作用故存在误差,特别是频率偏离谐振频率。在LLC谐振电路中的谐振腔本身具有选频特性,对3次以上的谐波呈现很高的阻抗。所以就 忽略高次谐波影响。
3.LLC串联谐振拓扑谐振腔电流:
举例1:
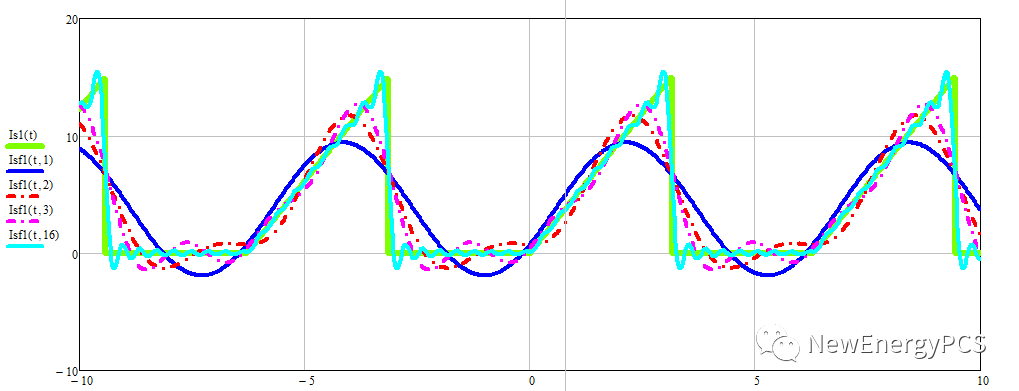
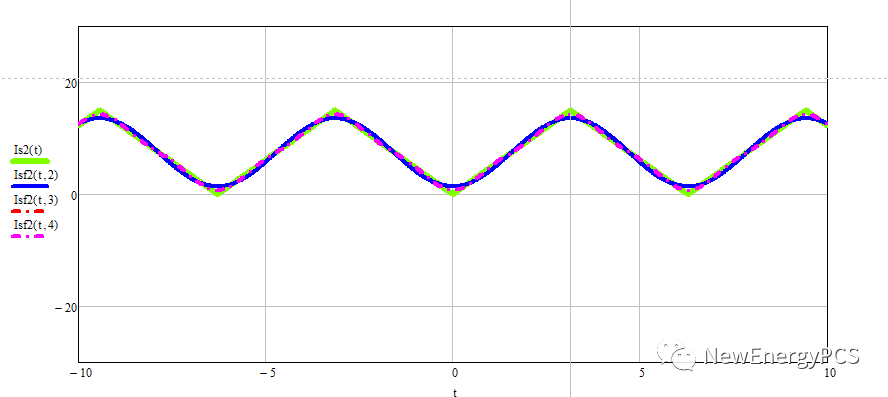
假设把上述的LLC半桥中点电压加在一个电感L上,得到电感电流波形。

可以看出电感加方波电压,电流逐渐上升,直到饱和,存在这个现象是因为磁没有复位。如果电感加傅里叶展开的波形,当包含7次谐波时,电流波形很接近。电流谐波次数越高就几乎完全一样了。
LLC谐振腔电流:
谐振腔网络的阻抗大小与工作频率有关,谐振网络的阻抗可能是容性,也可能是感 性,所以谐振电流的相位有可能超前电压(容性),或滞后电压(感性);所以电路可以由两部份构成,无相位差的纯阻性负载电流和有90度相位差的容性、感性谐振元件的无功电流相加的和。
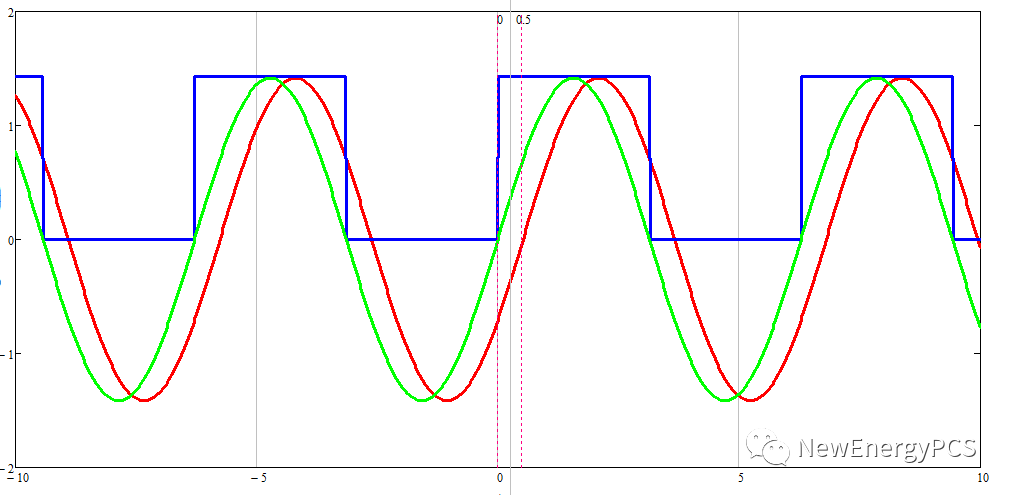
半桥谐振基波电压与基波电流的相位差

全桥谐振谐振基波电压与基波电流的相位差****
FHA就是假设加在谐振腔是正弦电压,相位和方波电压同相位,这样相位差就很明显了,得到了ZVS ZCS 就是利用电压与电流的相位差实现的。
举例2:
BUCK电路,电感两端的电压是Vin-Vo(开关导通),续流时电 感两端的电压是 -Vo(开关关短,续流管导通)。

Buck-CCM电感电压电流波形
Buck-DCM电感电流波形
Buck-BCM电感电流波形
FHA 基波分析法展开buck电路波形。CCM模式下的电感电流可以看成叠加了直流偏置,不影响分析。这样就诠释了电感电流滞后电压90°
4.LLC串联谐振拓扑的特性曲线:
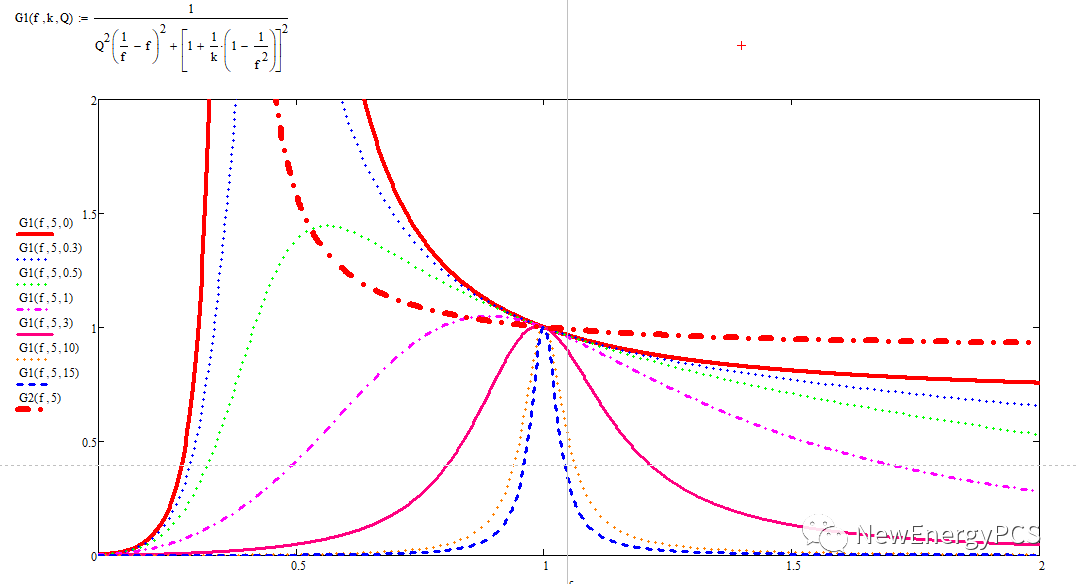
通过LLC 串联谐振网络等效电路,用其前向传递函数。可以得到归一化的电压增益曲线。
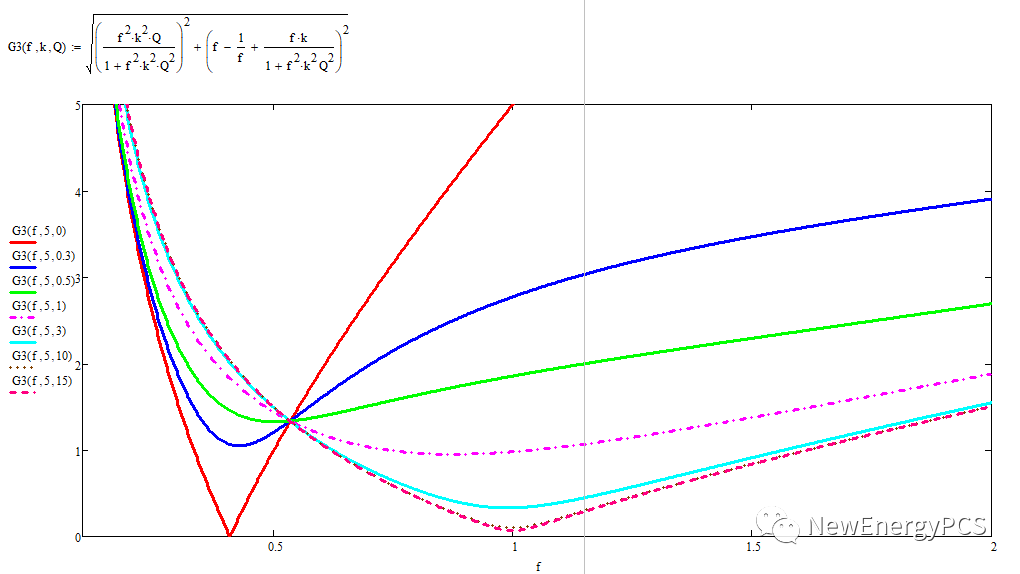
通过输入阻抗与特征阻抗Z0可以得到归一化的输入阻抗曲线。
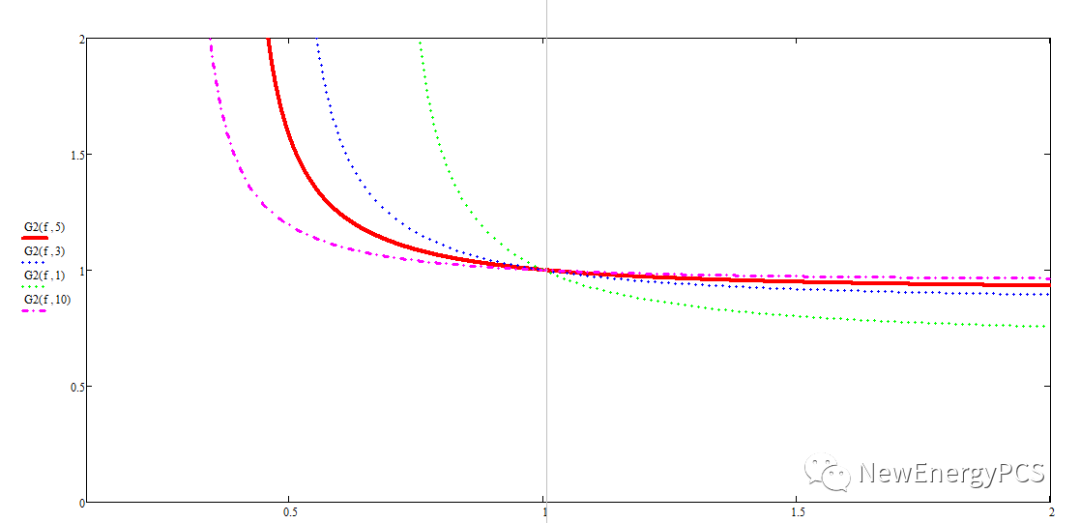
电路虚部为零,可以得到阻性分割线曲线。
-
什么是光学谐振腔?2024-03-15 2158
-
LLC谐振腔损耗怎么仿真?2023-10-22 1560
-
什么是光学谐振腔?光学谐振腔的作用有哪些?2023-09-14 5087
-
开关电源的LLC谐振拓扑结构2023-03-17 19298
-
【干货分享】LLC谐振半桥电路分析与设计2021-07-24 5996
-
谐振腔的作用2018-12-18 31067
-
LLC相关知识-谐振的基本概念2018-07-19 2629
-
MOSFET电容在LLC串联谐振电路中的作用2018-07-18 4403
-
MOSFET寄生电容对LLC串联谐振电路ZVS的影响2018-07-13 5656
-
基于MATLAB光学谐振腔的设计2017-11-03 2706
-
LLC谐振腔半桥变压器设计问题2017-09-07 1867
-
光学谐振腔基本概念2011-01-05 1850
-
传输型谐振腔理论2009-11-03 3356
全部0条评论

快来发表一下你的评论吧 !

