玻璃基集成光量子芯片的研究进展

文章来源：中国物理学会期刊网 原文作者：李萌 李础 李焱     

摘要   玻璃基集成光量子芯片已经应用于量子计算、量子模拟、量子通信、量子精密测量等光量子信息处理领域，显示出强大的功能。文章从量子计算和量子模拟两个方面介绍利用飞秒激光三维高精度直写技术在玻璃中制备集成光量子芯片的重要进展。量子计算芯片包括面向通用量子计算的单比特到多比特光量子逻辑门以及用于解决特定问题的芯片，可实现玻色采样、量子快速傅里叶变换、量子快速到达等功能。在量子模拟方面，玻璃基光量子芯片成为研究关联粒子量子行走动力学和拓扑量子光子学的极佳平台，揭示了一维、二维和合成维度的离散以及连续时间量子行走的演化规律，展示了光子拓扑绝缘体的鲁棒性拓扑模式对量子态传输的保护作用等。

  1  引 言    

近年来，集成光量子芯片由于具有可扩展性强、稳定性高、便携小型化等优势，取得了突飞猛进的发展，其中基于飞秒激光直写技术制备、可实现三维架构、多自由度集成的光子芯片与光量子技术相结合构成的玻璃基集成光量子芯片受到了关注。如今，玻璃基集成光量子芯片已经被广泛应用于量子计算[1—4]、量子通信[5，6]、量子精密测量[7，8]和量子模拟[9—11]等多个领域。本文将重点介绍近几年玻璃基光量子芯片在量子计算和量子模拟领域的重要进展(图1)[12—16]。

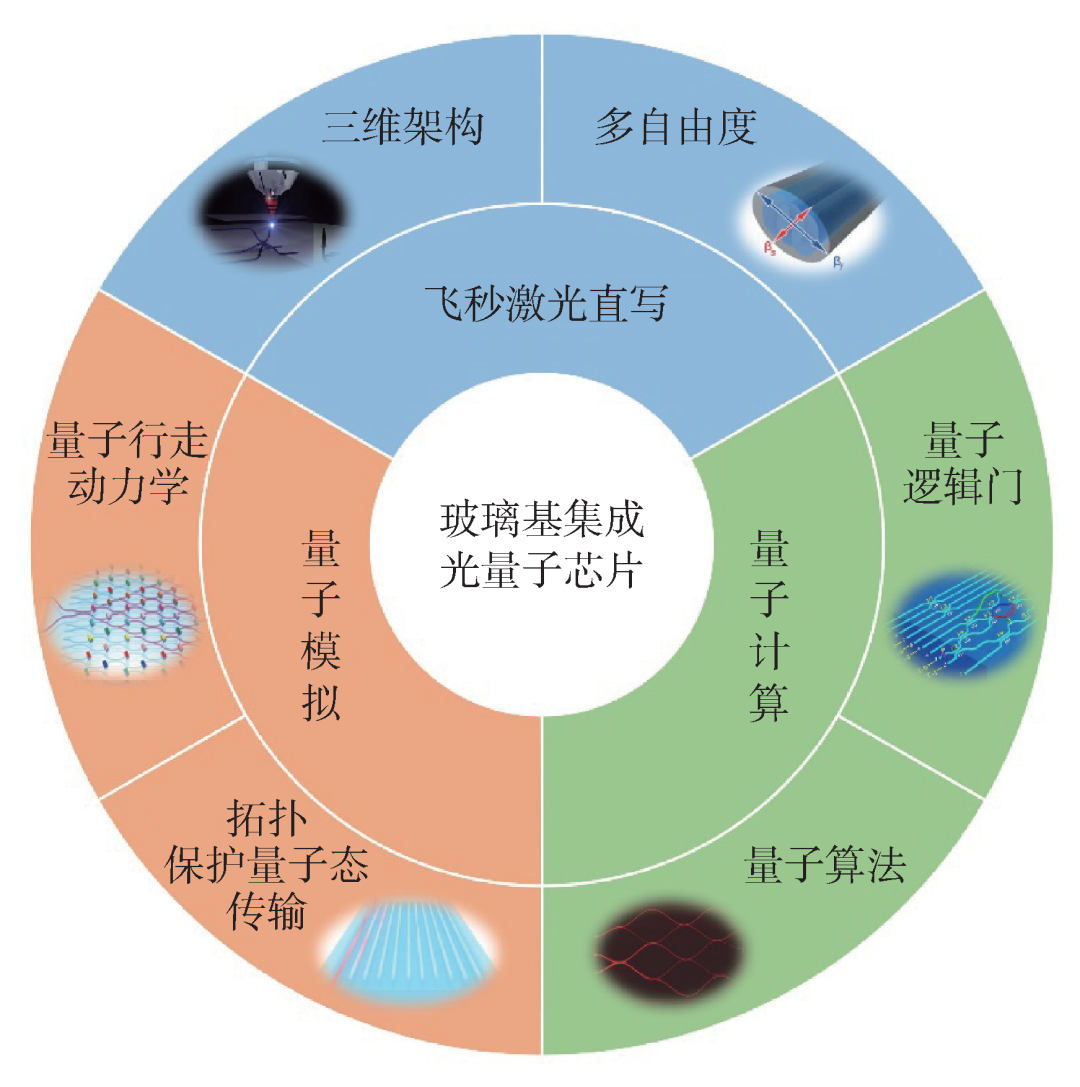
图1 飞秒激光直写的玻璃基集成光量子芯片及其应用[2，12—16]

1996年，Davis等人首次发现将飞秒激光脉冲聚焦到玻璃内部可以引起折射率增大的现象，并应用于玻璃内部光波导的制备[17]。2009年，Withford课题组首次利用飞秒激光直写技术在熔融石英玻璃中制备出波导定向耦合器(图2(a))，并利用量子光源进行了双光子、三光子量子干涉实验的表征，拉开了玻璃基量子集成光学研究的序幕[18]。飞秒激光直写技术可以提供近圆形的波导截面和模场[19]，从而支持两种正交偏振模式的传输(图2(b))，因此在进行片上量子信息处理时既可以支持路径编码，又可以支持偏振编码。凭借其内禀的真三维直写能力，该技术可以灵活地制备具有复杂线路、三维结构的光量子芯片，在量子计算和量子模拟的应用中显示出强大的功能，不仅可以简化线路设计和减少所需线性光学元件的数量[20，21]，而且可以研究一些二维的光子演化和分布问题[22]，此时将第三维用于时间演化。比如图2(c)所示的三维光波导结构，既可以基于光子模式实现任意子非阿贝尔编织过程的量子模拟，又可以为拓扑保护光量子计算提供新的技术方案[23]。此外，通过多次扫描和横向堆叠，利用飞秒激光直写技术制备的环状波导还可以支持涡旋光束的传输(图2(d))[24，25]，丰富了片上可调控的光子自由度。

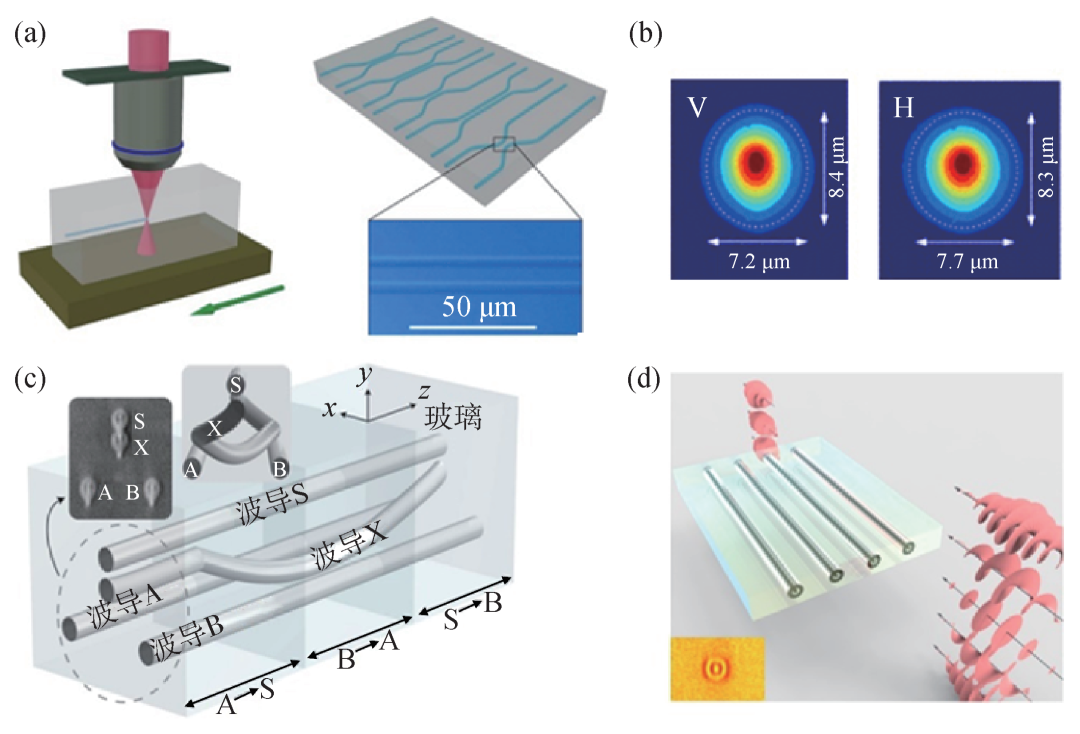
图2 飞秒激光直写在玻璃内部制备的光波导器件    (a)在玻璃内部直写的光波导(左图)以及由光波导构成的不同相互作用长度和相互作用距离的定向耦合器(右图)，其中插图为放大后的耦合区显微图[18]；(b)波导模场分布，支持垂直方向(V)和水平方向(H)两种正交偏振模式[19]；(c)利用光子模式模拟任意子非阿贝尔编织的三维光波导单元结构[23]；(d)环状波导传输涡旋光束。携带不同轨道角动量的光子(右下)通过芯片后，其模式会被转换为环状波导所支持的低阶轨道角动量模式(左上)。左下插图为环状波导截面显微图[24，25]

  2  玻璃基三维光子集成芯片的制备    

利用聚焦的飞秒激光脉冲在透明介质材料中直写光波导时主要采取横向直写方式，因为其在制备具有三维结构的光波导时具有更好的灵活性。然而，横向直写方式在制备不同深度的三维光波导时，会由于空气/玻璃界面折射率失配造成的球差导致加工焦斑畸变和偏离设定位置的问题(图3(a))，破坏波导的对称性和均匀度[26]。球差显著依赖于聚焦深度和聚焦物镜的数值孔径，图3(a)中就分别展示了在不同数值孔径下，聚焦光斑的峰值强度(图3(a-ii))和沿传输方向的半高全宽(图3(a-iii))随聚焦深度的变化[26]。随着聚焦深度的增加，峰值强度在降低，半高全宽在增大，数值孔径越大越敏感，而在低数值孔径情况下二者在一定深度范围内变化较缓。

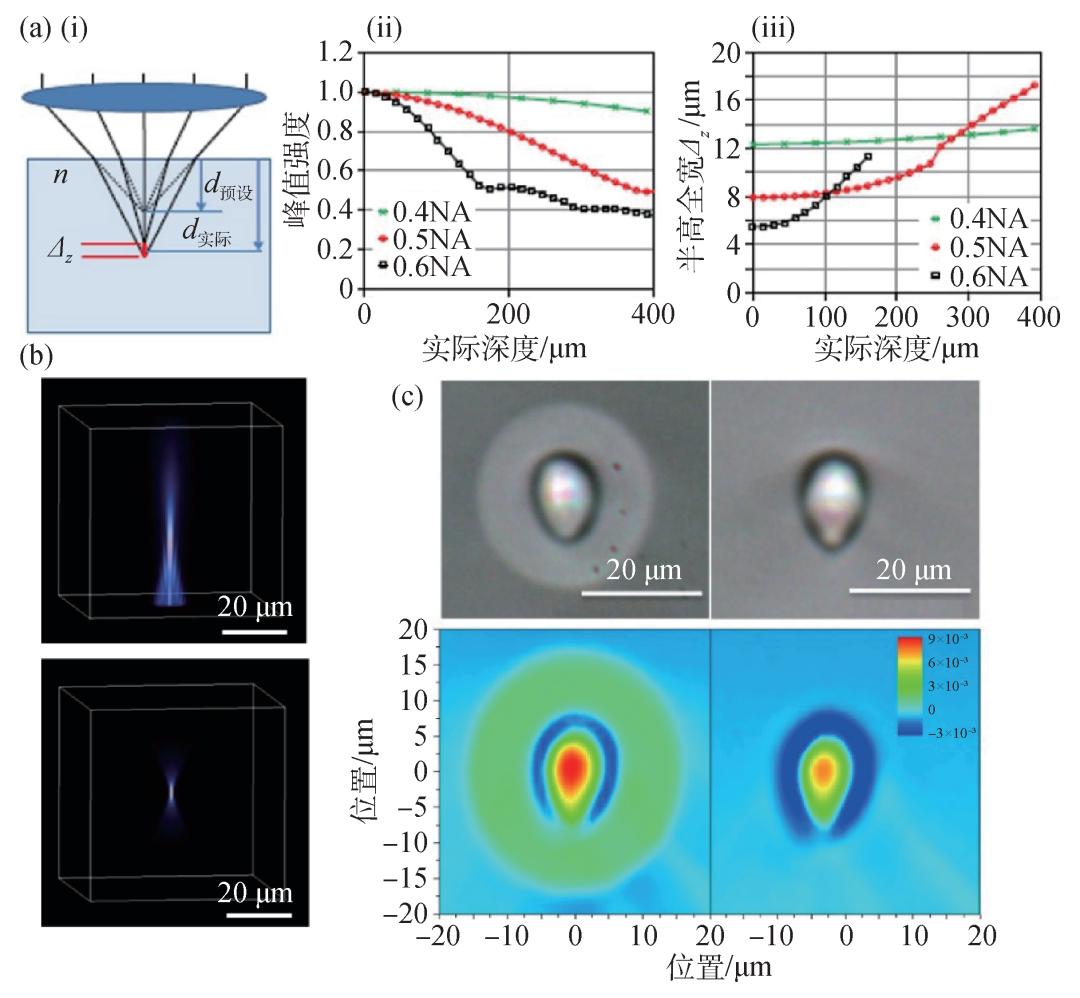
图3 飞秒激光直写方式制备深度变化的三维光波导    (a-i)界面折射率失配带来的球差示意图，以及不同数值孔径(NA)下，聚焦光斑峰值强度(a-ii)和沿传输方向分布的半高全宽随聚焦深度的变化(a-iii)[26]；(b)未预补偿球差(上图)和预补偿球差(下图)时，聚焦光斑在表面以下200 μm深度处的形貌[27]；(c)多次扫描后，热退火前(左)和后(右)的波导截面形貌(上)和折射率分布(下)[28]

利用较低数值孔径(如NA=0.4)的物镜加工，虽然波导截面纵横比较大，即使不进行球差校正，也可以在一定深度范围内直写出性能相近的光波导。而利用较高数值孔径(如NA=0.8)的物镜加工，如果不补偿球差，在聚焦深度为玻璃表面以下200 μm时，焦斑就会发生拉伸畸变，如图3(b)中的上图所示；如果在空间光调制器上加载预补偿相位，可以使聚焦光斑的形貌基本保持不变[27]，如图3(b)中的下图所示。一般情况下，在小于800 μm深度范围内，预补偿相位可以消除界面折射率失配带来的球差。然而该方法只适用于在离散的深度处逐点补偿能量和相位，并不适用于在连续大深度变化情况下直写均匀的三维光波导，这是目前直写制备复杂线路三维光量子芯片遇到的挑战。

借鉴天体光子学中光瞳重排器的制备经验[28，29]，利用多次扫描和热退火两步方案可以在一定深度范围内解决该问题。选择合适数值孔径的聚焦物镜，确定加工单脉冲能量和扫描速率，先通过原位多次扫描制备出折射率对比度较高、截面尺寸较大的多模光波导，再通过热退火的处理方法消除外环折射率修饰和激光诱导的残余应力分布(图3(c))，虽然折射率对比度稍微降低，却可以制备出具备传输损耗低和双折射低的单模光波导。这种光波导不仅可以支持更小的弯曲半径，还可以在更大的连续深度变化范围内保持波导性能一致。导光波长则可以通过扫描次数、单脉冲能量和扫描速率等参数来控制。该方法为制备三维、紧凑、高效的集成光量子芯片提供了可能。

  3  玻璃基光量子计算芯片    

利用飞秒激光直写技术制备的玻璃基集成光量子芯片具有很多种基本元件，比如双端口和多端口的定向耦合器[30，31]、偏振依赖的部分偏振定向耦合器[1]、偏振不敏感定向耦合器[19]、几何变形控制的被动相移器[32]、可电热调谐的主动相移器[33]等。将这些基本元件按照量子线路进行组合，再结合真三维直写能力，就可以制备出各种功能丰富的玻璃基光量子计算芯片，比如光量子逻辑门和光量子算法芯片。    

3.1 光量子逻辑门

量子逻辑门是构建通用量子计算线路的基本单元。理论上，任意的多量子比特门都可以由一系列单量子比特门和两量子比特门构成[34，35]。2001年，Knill、Laflamme、Milburn(KLM)三人研究发现，利用线性光学元件、单光子源和单光子探测器，就可以实现线性光学量子计算[36]，使概率门、可预报门以及逻辑门级联成为可能。但是，直接基于KLM方案的多量子比特门有时需要消耗大量的光子和光学元件资源，因此在实际制备中仍需要对线路进行合理优化。

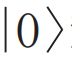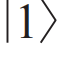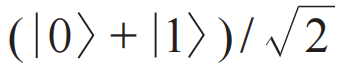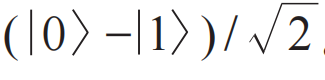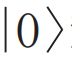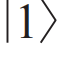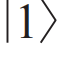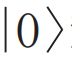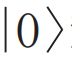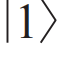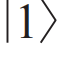最基本的量子逻辑门是单量子比特门，比如阿达玛门(H门)和用泡利矩阵描述的X、Y、Z门。H门的作用是将输入态和分别转化为叠加态和。X门的作用是将量子比特逻辑状态翻转，比如将()翻转为()。Y门的作用则是将()转换为i (-i 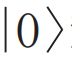)。Z门可以实现π相位翻转，使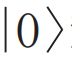保持不变，使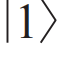转换为-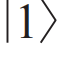。基于飞秒激光直写技术，几种重要的单量子比特门已经被制备出来，比如偏振编码的H门和X门，都可以通过改变波导光轴实现。在原直波导附近添加一条损伤线，通过诱导应力场改变波导的光轴，控制损伤线的长度、方位以及与波导的间距，就可以实现不同的量子门[37]。此外，将入射光束偏离物镜入瞳中心一定距离，使聚焦后的出射光束偏离竖直方向一个夹角，所直写的波导的光轴也存在一个与之相近的倾斜角，进一步控制光轴倾斜波导的长度，构成波导波片[38]，也可以实现不同的单量子比特门。而路径编码的单量子比特门，可以依托电热调谐的马赫—曾德尔(MZ)干涉仪结构实现任意的单量子比特门操作。

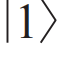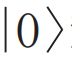两量子比特门中最重要的就是受控非门(CNOT门)，它是在众多量子逻辑门线路分解中出现最多的两量子比特门。CNOT门的功能是，当且仅当控制比特逻辑状态为时，目标比特逻辑状态才发生翻转，即()，而当控制比特逻辑状态为时，目标比特逻辑状态保持不变。而且CNOT门和受控相位门(CZ门)可以通过在目标比特输入、输出端各增加一个H门实现转换。基于飞秒激光直写技术，偏振编码的CNOT门和可预报CNOT门[1，39]，路径编码的CNOT门和可预报CZ门(hCZ门)已经被制备出来[20，40]。图4(a)展示的是一种利用三个部分偏振定向耦合器(PPDC)构成的偏振编码的概率性后选择CNOT门[1]。线路中起主要作用的是PPDC1，而PPDC2和PPDC3只是起到振幅补偿的作用。此外，利用完全偏振定向耦合器和纠缠光子源，也可以实现偏振编码的可预报CNOT门[39]。图4(b)是一种路径编码的hCZ门[20]。得益于飞秒激光直写技术的真三维直写能力，三维的线路设计巧妙地避免了线路中的波导交叉。2019年，我们制备了路径编码的两量子比特CNOT门[40]。在此基础上，通过将H门和CNOT门控制比特级联，制备了可分别产生四种路径编码贝尔态的逻辑门组合芯片[41]，如图4(c)所示。其中蓝色部分的定向耦合器代表H门，其余部分代表路径编码的CNOT门。H门的作用是产生叠加态，CNOT门则是起到纠缠作用。路径编码CNOT门的工作原理是经典MZ干涉和量子Hong—Ou—Mandel(HOM)干涉的联合作用，由量子干涉引入π相位，控制经典MZ干涉仪的输出状态。制备高性能、高保真度的两量子比特门是制备线路复杂的多量子比特门的基础。

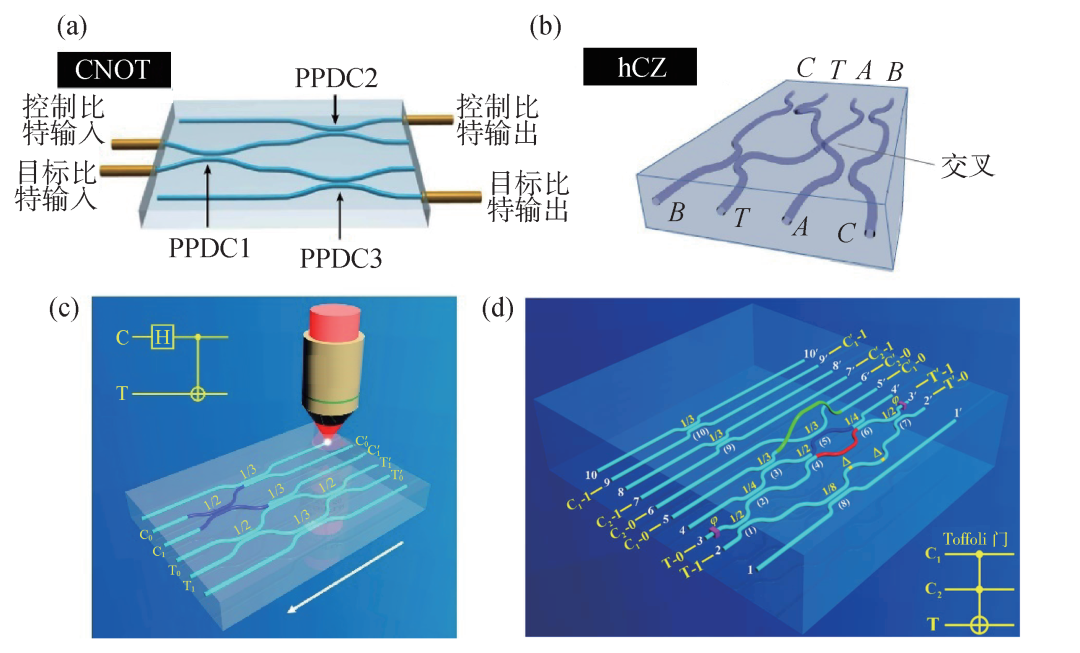
图4 飞秒激光直写制备的多种光量子逻辑门    (a)偏振编码的CNOT门[1]；(b)路径编码的hCZ门[20]；(c)路径编码的H门和CNOT门组合芯片实现路径编码贝尔态的制备[41]；(d)具有三维构型的路径编码三量子比特Toffoli门[14]

三量子比特Toffoli门是最重要的多量子比特逻辑门之一，可以和H门构成一个简单的通用量子门集合，实现更复杂的量子逻辑与算法，在量子纠错、量子搜索等线路中扮演重要角色。Toffoli门也称为受控—受控非门(CCNOT门)，包含两个控制比特和一个目标比特，其逻辑功能是当且仅当两个控制比特均为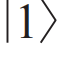时，目标比特的逻辑状态才发生翻转，即和。按照传统量子线路分解，要实现量子Toffoli门一般需要6个两量子比特CNOT门和10个不同类型的单量子比特门，不仅线路复杂，而且操作成功率很低。2022年，我们以概率性后选择受控—受控相位(CCZ)门为核心制备出首个玻璃基量子Toffoli门(图4(d))[14]，采用路径编码并将目标比特由传统的二能级的“qubit”更换为三能级的“qutrit”，仅需要2个级联的CZ门和3个信号光子，无需附属光子，并且操作成功率也提高至1/72[42]。其中的关键，是引入深度变化的三维立交桥状波导，消除了与其他波导间很难避免的交叉和耦合，将二维量子线路优化为更简洁的三维构型，大大提升了芯片的性能。所制备的量子Toffoli门芯片中量子干涉最多仅需1次，因此能够获得较高的真值表保真度，实测值为85.5%。此外，还展示了利用两个立交桥状波导方案制备路径编码四量子比特受控—受控—受控非(CCCNOT)门的潜力，巧妙地规避了波导之间所有不必要的交叉和耦合，进一步凸显了三维量子线路的优越性，为实现线路更复杂、功能更强大的玻璃基光量子计算芯片奠定了技术基础。

  3.2 光量子算法芯片

玻璃基光量子芯片已在解决特定量子问题，比如玻色采样、量子快速傅里叶变换、量子快速到达等得到应用。

玻色采样，是将多个无相互作用的全同玻色子输入线性多模干涉仪(对应一个哈尔随机幺正变换矩阵)中，求解玻色子的输出概率分布。光子是玻色子，在演化过程中会发生非经典干涉，如果要求解演化后的多光子态分布就需要计算幺正矩阵子矩阵的积和式，而理论上这类复杂的计算问题无法在多项式时间内有效解决。当参与演化的光子数和线性多模干涉仪达到一定规模时，玻色采样专用光量子系统就可以展现出光量子计算的强大威力和相较于经典计算的绝对优势。玻璃基玻色采样光量子芯片可以很好地求解这类问题，而且凭借三维架构可以在很小的空间大幅提高其扩展规模。图5(a)展示的是一种离散耦合玻色采样光量子芯片[2]。芯片内部含有8个定向耦合器(η)和11个相移器(φ)，共计19个随机参数，构成了一个随机网络，实验中可操控的输入光子数为3个，这些参数组合已经可以充分展示玻色采样的复杂性。图5(b)展示的是一种可重构的三维连续耦合玻色采样光量子芯片[43]，其中32根波导按照8×4阵列排布，由相对正三角形晶格位置分布的随机调制引入耦合系数的随机性，并且芯片顶部制备的16个可电热调谐相移器可以快速地调制波导的折射率及传播常数，实现不同的变换，使芯片具有高度可重构性。该芯片已经成功演示验证了3光子和4光子玻色采样实验，为更大规模的光子玻色采样提供了可能。除此之外，以降低实验难度并提高计算复杂度为目标的多光子多模式的玻璃基玻色采样光量子芯片不断涌现，比如时间戳玻色采样[44]、忆阻器玻色采样等[45]。

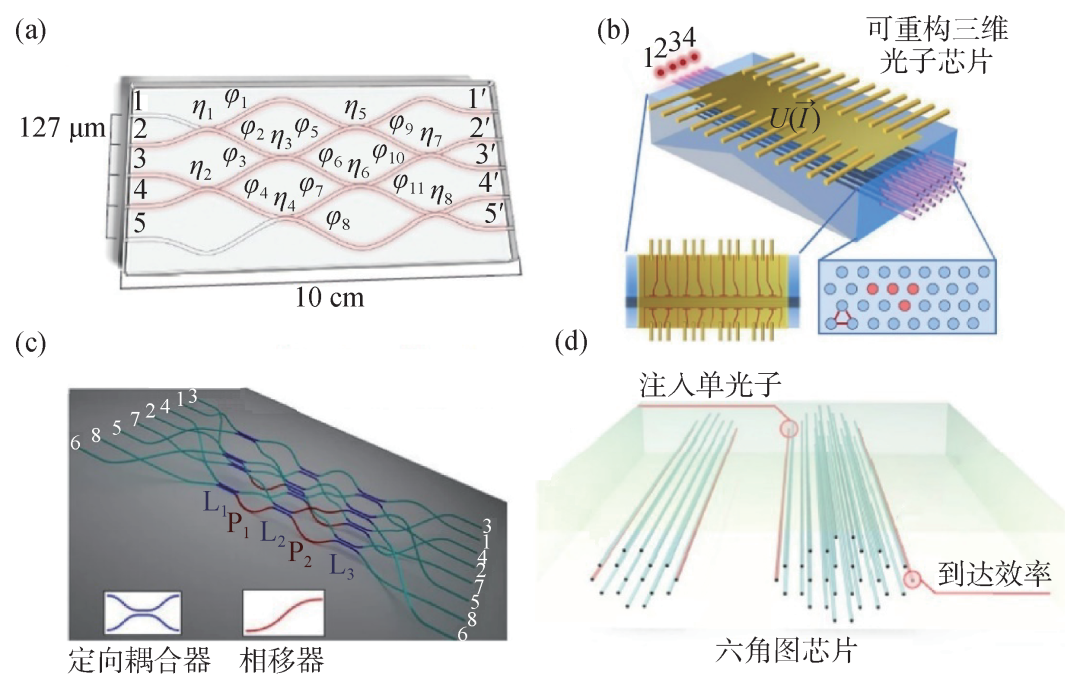
图5 基于飞秒激光直写制备的光量子算法芯片    (a)离散耦合玻色采样[2]；(b)可重构连续耦合玻色采样芯片[43]。左下插图是芯片顶部控制电热相移器的电子线路的俯视图，右下插图是波导阵列截面示意图，其中标红的位置代表注入光子的波导；(c)8模量子快速傅里叶变换算法芯片[21]；(d)量子快速到达算法[46]

量子傅里叶变换是经典离散傅里叶变换的量子对应，是多种量子算法的核心模块。2016年，Crespi等人制备了基于模式编码的8模量子快速傅里叶变换(qFFT)算法芯片(图5(c))，观测到了双光子干涉的零透射抑制定律[21]。该芯片的线路根据立方体的顶点和边的连接关系特别设计，其中顶点代表波导模式1—8，边代表2波导模式之间的H门变换，相移由连接前后2个定向耦合器的弯曲波导几何变形实现。在这种三维路径设计下，可以避免平面波导排布时出现的大量交叉，将所需定向耦合器的数量从传统线路的28个减少到12个。

基于量子行走的天然叠加态特性而实现的量子快速到达算法，在解决粘合树问题上展现了比经典随机行走更快的到达速度。2018年，金贤敏课题组成功将该粘合树图结构以几何可扩展的方式映射到三维光子芯片上[46]，如图5(d)所示。他们在节点数多达160个和深度为8层的结构中利用单光子二维量子行走实验展示了量子快速到达算法，证明了最佳到达时间和网络深度呈线性关系。此外，在处理更多分支、更大深度甚至更高维度的粘合树问题时，还可以考虑将其映射到等效的一维波导阵列结构去解决[47]。

  4  玻璃基光量子模拟芯片    

量子模拟是利用与待研究的量子问题相似或相关的人工可控的量子系统来模拟对应未知或难以控制的量子体系，通过观测给出定量或定性的结论。在飞秒激光直写的三维光波导耦合阵列结构中，光场在波导中的传输方程与量子力学中的薛定谔方程具有相似性，因此光场在波导阵列中的传输类似于电子或其他准粒子在凝聚态物理系统(如晶格、准晶、无序系统)中的传播。基于耦合光波导阵列的哈密顿量和传播方程可以对一些凝聚态物理系统的基础模型进行量子模拟[48]。量子光源所产生的单光子具备量子态叠加性，而所产生的关联光子对具有非经典关联，可以模拟两体或多体之间的量子关联。

三维耦合光波导阵列与量子光源相结合构成的玻璃基集成光量子模拟平台具有显著优势：(1)可以模拟单粒子和关联粒子在二维空间的量子随机行走动力学演化，而且能大幅扩展模拟体系的规模；(2)可以模拟凝聚态物理模型中的多种拓扑绝缘体结构，并研究受拓扑保护的量子态传输过程；(3)还可以充分利用光子的路径、模式、偏振和轨道角动量等多种自由度，模拟研究关联粒子在高维空间和复杂体系中的量子物理现象和规律。

    4.1 量子行走动力学

量子行走模型不仅可以用于实现量子计算，其本身也是一个重要的量子模拟平台[49]。单粒子和关联粒子的量子行走动力学非常适合用飞秒激光直写的集成光量子芯片进行模拟，不仅可以研究连续时间、离散时间量子行走，还可以研究一维、二维以及合成维度的量子行走演化规律。

图6(a)是2013年Crespi等人制备的一维离散时间量子行走干涉仪网络芯片，由大量偏振不敏感的定向耦合器和引入随机参数的相移器构成，相比于体光学系统具有更好的稳定性和更大的扩展规模。输入端注入的是偏振纠缠双光子，可以根据波函数的对称和反对称分别模拟玻色子和费米子在无序体系中的量子行走演化，最终输出端的光子符合计数展现了不同性质的安德森局域化现象[15]。图6(b)是2018年金贤敏课题组制备的超大规模(49×49)二维连续时间量子行走光子芯片，模拟了单粒子行走者在真实二维空间的量子随机行走演化规律。在中心格点波导注入单光子作为行走者，输出端面与触发光子符合的单光子数量表示的演化图案具有弹道形状的分布，明显不同于经典随机行走演化图案的高斯型分布[22]。2021年，金贤敏课题组又演示了关联光子对在二维波导晶格中的量子随机行走演化(图6(c))，将其对应到一个37×37的高维空间，实现了更大状态空间中的信息编码和高维图的构建，在实验中探测到600多个非经典干涉现象，进而观测到了违背经典关联的量子关联特性[50]。除此之外，偏振作为光子的一个重要自由度，也为量子行走的模拟提供了更多可能。2021年，Ehrhardt等人将光子的偏振引入量子行走模拟实验中，利用具有特定双折射的波导中关联光子对的空间和偏振两个自由度的杂化以实现合成维度，降低了实验的实现难度，从而完成了与复杂图网络对应的三维量子行走实验[13]，如图6(d)所示，为探索复杂的费米子量子行走和双层二维材料的量子动力学提供了可能。

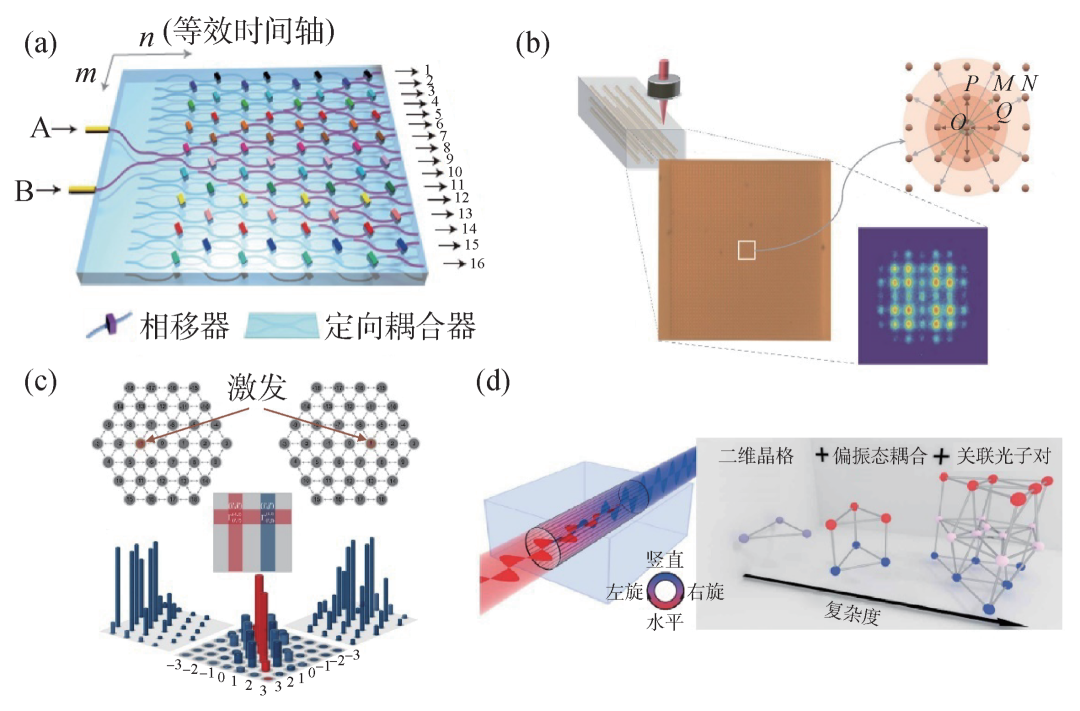
图6 利用飞秒激光直写制备的模拟光量子行走的芯片    (a)一维离散时间量子行走，注入光源为偏振纠缠双光子[15]；(b)二维连续时间量子行走，注入光源为单光子[22]。右上插图展示了晶格中波导之间各种耦合作用，右下插图展示了单光子在晶格中量子行走后所输出的演化图案；(c)关联光子对的二维连续时间量子行走[50]。将一对关联光子分别注入到晶格中心左右2个对称的格点，输出端的单光子概率分布分别如左下和右下2张图所示，下方中间图表示的是两光子在晶格内部发生量子干涉后，在输出端面由符合计数得到的归一化符合概率，反映了两光子的量子关联，红色部分对应两光子在同一格点聚束，蓝色部分对应两个光子分布在不同的格点；(d)引入偏振作为合成维度的关联光子对量子行走[13]。左图表示具有特定双折射的波导可以实现水平(红色)和竖直(蓝色)偏振模式的相干耦合。右图表示由空间位置代表的平面图结构，因两种偏振态的耦合而获得额外的维度，变成双层图结构。当注入的是关联光子对时，光子对的状态空间就要用复杂的三维图来表示

    4.2 拓扑保护量子态传输

2013年，Rechtsman等人制备了基于螺旋光波导晶格的光子弗洛凯(Floquet)拓扑绝缘体[51]，实现了对凝聚态物理模型中的拓扑绝缘体结构的量子模拟。伴随光量子技术的发展，最新的实验研究发现，光子拓扑绝缘体可以为单光子、关联光子、纠缠光子、压缩态光子的量子态传输过程提供拓扑保护，使其免疫于晶格缺陷和无序，有望用于增强集成光量子信息处理技术中。

紧束缚一维Su—Schrieffer—Heeger(SSH)晶格模型是最为经典的拓扑绝缘体模型之一，可以很好地用耦合光波导阵列模拟。根据相邻波导之间耦合强度参数(耦合间距)的不同配置，可以分为拓扑平庸和拓扑非平庸的光波导晶格。在图7(a)所示的一维SSH波导晶格中，波导1—10对应的是拓扑非平庸晶格(宽-窄-……宽-窄-宽)，支持拓扑边界模，波导11—20对应的是拓扑平庸晶格(窄-宽-……窄-宽-窄)，无拓扑边界模，将这两种晶格组合会在界面产生缺陷模。拓扑边界模和界面缺陷模都会将光场强约束在拓扑保护通道中，分别对应于1和10号波导。在脉冲光泵浦下，熔融石英玻璃芯片中受拓扑保护的波导内发生了非线性四波混频过程，在弱泵浦机制下，产生一对频率关联的闲频光子和信号光子；在强泵浦机制下，光子对产生过程的高阶项占主导，就会产生压缩光。对比不同演化长度下波导(1，10，20)中双光子量子关联度以及压缩光的压缩参数可知，拓扑非平庸边界态和拓扑界面缺陷态对关联光子和压缩光都具有拓扑保护作用[52]。

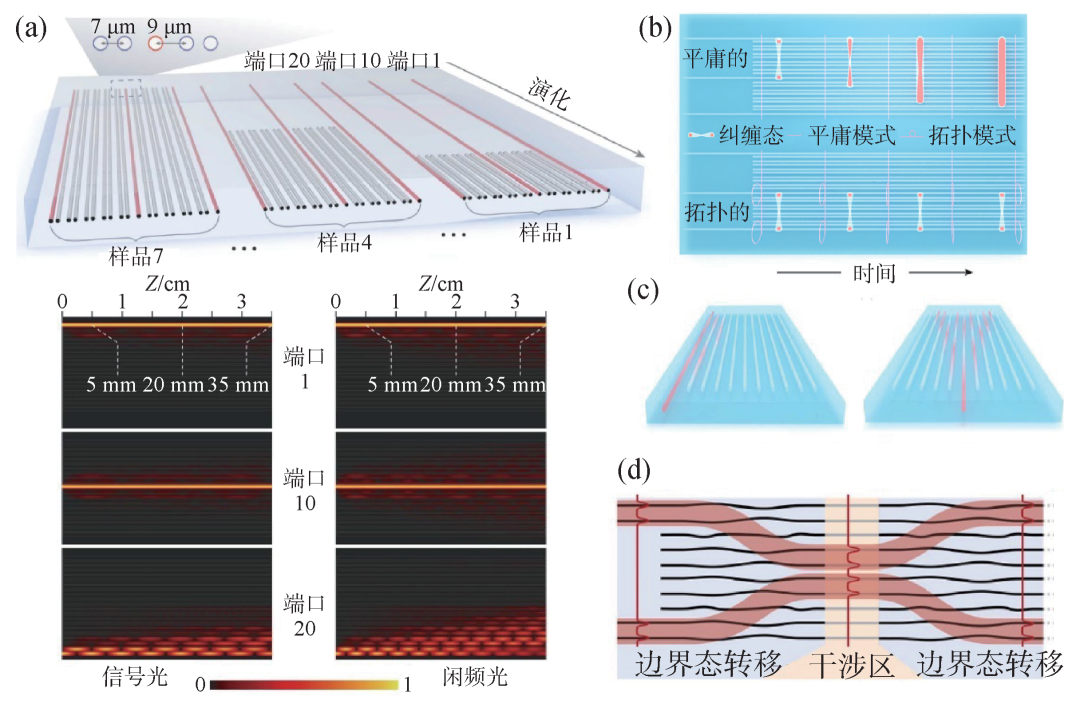
图7 一维光子拓扑绝缘体中的量子态传输      (a)在一维SSH模型的光波导晶格中，拓扑非平庸边界态、拓扑界面缺陷态对产生的关联光子和压缩光的空间分布、量子关联及压缩参数具有拓扑保护[52]。下方图中关联光子对在不同通道中的演化结果表明，信号光子和闲频光子的模式可以被局域在拓扑保护通道(1和10)中，但在非拓扑保护通道(20)中却出现明显的扩散；(b)在一维SSH模型的光波导晶格中，拓扑边界态对偏振纠缠光子的量子关联和纠缠并发性具有拓扑保护[53]；(c)基于一维非对角AAH模型的光波导准晶中，拓扑边界态(左)对双光子量子态具有拓扑保护，而体态(右)不具备[16]；(d)在一维非对角AAH模型的光波导准晶中，两侧单光子拓扑边界态通过绝热演化相互靠近，发生了量子HOM干涉[54]

偏振纠缠态是光量子信息处理实验中最为经典，也是应用最为广泛的纠缠资源。如图7(b)所示，同样基于一维SSH模型，在玻璃基光子芯片上将处于偏振纠缠态的一对光子分别注入到拓扑缺陷模和拓扑非平庸模(平庸模)对应的波导中，通过量子过程层析，可以看到随着演化长度的增加，拓扑非平庸模的光子偏振纠缠态的交叉关联函数和并发性都几乎保持不变，而拓扑平庸模对应的物理量都呈指数衰减。由此可见，拓扑非平庸模式很好地保护了光子偏振纠缠态，而并发性的微弱降低源于弱测量效应，是波导中两正交偏振光子在波导间的耦合差异造成的[53]。

一维非对角Aubry—André—Harper(AAH)准晶模型所支持的拓扑边界模也常被用于拓扑保护的量子态传输。在非对角AAH模型中，相邻波导间的耦合强度是按余弦调制的，而飞秒激光直写技术可以精确控制相邻波导的耦合间距来控制耦合强度，因此该模型也可以利用玻璃基光子芯片进行模拟。如图7(c)所示，将具有量子关联的双光子分别注入基于非对角AAH模型波导准晶的边界格点和中心格点，可以分别激发拓扑边界态和体态。拓扑边界态的双光子量子关联保持和输入时一致的高水平，且不受光子可分和不可分性质的影响；而体态的双光子量子关联则明显下降[16]。如图7(d)所示，调制非对角AAH模型中相邻波导间的耦合参数，可使原本束缚在两侧边界的单光子拓扑边界态绝热演变而被拉近到中心处，发生量子HOM干涉，产生聚束效应，然后再通过绝热演变回归到两侧边界。实验结果显示，单光子拓扑边界态的量子干涉可见度相比初始值可以高达98.5%，为利用拓扑光子学增强光量子信息处理技术提供了可能[54]。

此外，玻璃基二维光子拓扑绝缘体的高阶拓扑模式也被用于量子态传输。图8(a)中芯片主体为基于紧束缚二维SSH晶格的光子高阶拓扑绝缘体。入射的单光子被三维的1分4耦合器均分成振幅和相位相等的四输入叠加态，然后被注入到光子高阶拓扑绝缘体的4个角格点，从而激发出零能角态(8(a)上图)。由于角态和体态的正交性，四角叠加态在不同的演化长度上都可以得到很好地保持，即使引入无序性，拓扑角态的束缚作用依然是鲁棒的(8(a)下图)[55]。在图8(b)中，将关联的双光子分别注入二维SSH晶格的两个角格点波导中进行传输，拓扑非平庸晶格的输出双光子符合计数是拓扑平庸晶格输出结果的60倍，证明了拓扑角态的强局域性。当输入的双光子经历HOM干涉形成双光子NOON态后，再将其注入到拓扑非平庸晶格的2个角格点波导中，输出双光子的干涉可见度还可以维持在90%以上，表明拓扑角纠缠双光子态的空间分布在拓扑非平庸晶格中传输时还可以高保真维持[56]。

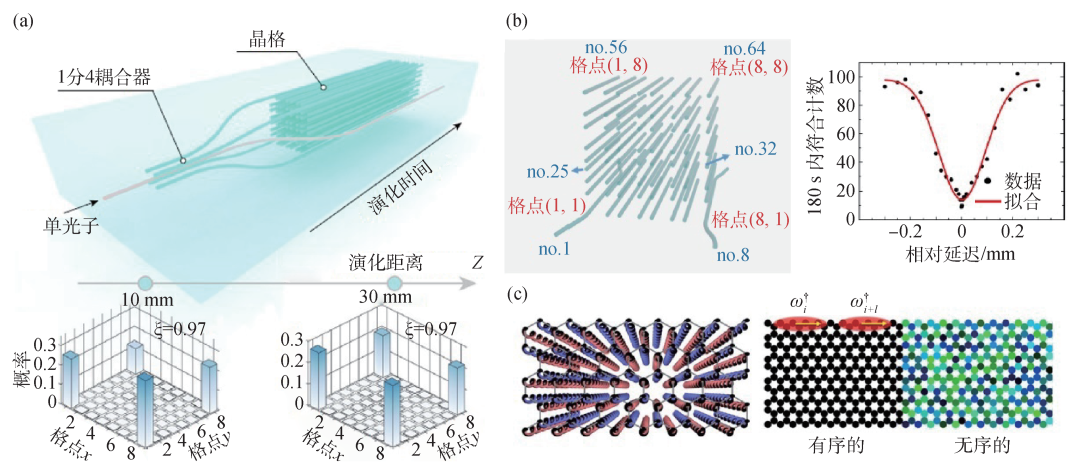
图8 二维光子拓扑绝缘体中的量子态传输      (a)单光子被三维的1分4耦合器均分成振幅和相位相等的四角叠加态，用于激发二维SSH高阶拓扑绝缘体零能角态，且叠加态空间分布不随演化长度变化。从图中可以看到四角叠加态传输10—30 mm后其空间分布仍几乎保持不变[55]；(b)拓扑双光子角态在左图所示的二维SSH晶格的角格点中传输，其量子干涉可见度可以高水平保持，如右图中量子干涉曲线所示[56]；(c)基于左图所示的螺旋波导蜂巢晶格光子Floquet拓扑绝缘体，双光子NOON态和反NOON态在右图中从有序区到无序区的拓扑边界传输过程可以免疫于体系的无序性[58]

到目前为止，实验上用于量子态传输的玻璃基光子拓扑绝缘体所利用的拓扑模式还局限在零维束缚模[11，16，52—57]，均无法展示单向、无背向散射拓扑边界传输模式对量子态传输的拓扑保护。2016年，Rechtsman等人从理论上证明了光子弗洛凯拓扑绝缘体的单向拓扑边界传输特性可以鲁棒地保护量子态传输免疫于体系的无序性[58]，如图8(c)所示，而拓扑平庸的一维螺旋波导阵列中NOON态量子关联被无序性破坏。这里的无序性是格点在位能的无序性，是利用波导折射率改变量的无序性来模拟实现的。该理论探讨的是量子纯态，但是结论也可以推广到混合态，而且实验上的若干技术难题也是可解决的。因此，利用玻璃基拓扑光量子芯片实现量子态的单向拓扑边界传输是极具潜力的。

  5  总 结    

基于飞秒激光直写技术制备的玻璃基集成光量子芯片，凭借其拥有的真三维构型和支持多种光子自由度的独特优势，在近些年兴起的量子集成光学领域大放异彩。无论是面向通用量子计算的光量子逻辑门，还是基于特定量子计算方案的芯片，都展现出玻璃基集成光量子计算平台的优越性。在量子模拟领域，基于量子行走原理的玻璃基光量子芯片提供了一个极佳的研究平台，所研究的问题可从单粒子、一维、单个自由度扩展到关联粒子、二维和多个自由度。将集成光量子技术与拓扑光子学相结合而发展的拓扑量子光子学，也在多种玻璃基光子拓扑绝缘体中实现，揭示了鲁棒拓扑模式对量子态传输的保护作用，可以用于增强光量子信息处理技术。

飞秒激光直写玻璃基集成光量子芯片走向实用化还面临一些挑战。由于飞秒激光直写诱导的折射率改变量较小（千分之几的量级），制备的波导的弯曲半径普遍较大（几十毫米），导致基本元件的纵向尺寸在毫米量级，级联单元越多，芯片纵向尺寸越长，越不利于大规模、高密度的集成。需要设计新型三维构型，并利用更多的光子自由度，以缩小元件尺度。玻璃基光量子芯片虽然也可基于热光效应进行调谐，但响应速度相对较慢，功耗也较高，深层波导的调谐工艺比较复杂。如果能将易调谐的二维硅基或铌酸锂基光量子芯片与玻璃基三维光量子芯片高效互连，解决互连中的损耗和模式不匹配等问题，就可以充分发挥两类芯片的优势，实现二维/三维混合集成的可调光量子芯片。

随着高性能量子光源和探测器以及飞秒激光直写技术的发展，玻璃基集成光量子芯片有望为大规模可扩展多比特光量子计算、多模式拓扑光量子计算、多光子拓扑量子态传输、多粒子系统量子模拟、多自由度量子态调控等提供技术支持，促进量子集成光学的快速发展和应用转化。

　　审核编辑：汤梓红