Sallen-Key低通滤波器的设计

01 Sallen-Key滤波器

一、背景介绍

近期由于需要测试所搭建的高阻抗信号源放大电路，其中包括有低通滤波器，所以研究了 Sallen-Key topology ^[1]^ 相关滤波电路电路。如下是 Kennth A. Kuhn 在 2016 给出的 Sallen-Key Low-Pass Filter ^[2]^ 设想步骤；2002年 TI 给出的 Analysis of the Sallen-Key Architecture ^[3]^ 应用报告，给出了不同 Kallen-Key 电路理论分析。

Sallen-Key 电子滤波器拓扑结构，由于其结构简单，被用于二阶有源滤波器电路设计，它是 VCVS（电压控制-电压输出）滤波器简化版本。VCVS 滤波器使用输入阻抗高、输出阻抗低的电压放大器来实现 2 个极点的低通、高通、带通滤波器。在不使用电感的情况下，可以获得高 Q 值，通带增益可调。多个 VCVS 滤波器可以直接级联形成高阶滤波器。Sallen-Key 滤波器则使用单位电压增益的放大器（俗称电压跟随器）设计的有源滤波器电路。

在1955年 R.P.Sallen，与 E.L.Key 利用了真空电子管阴极跟随放大器-具有近似单位电压增益电路设计滤波器。现代电子线路中则是普通的运算放大器进行设计，简单情况下，使用晶体管发射极跟随或者源极跟随器进行设计。

二、电路分析

虽然 Sallen-Key 电路结构可以形成不同特性的滤波器，由于后面实验需要，后面仅仅对低通滤波器设计进行讨论。下图是单位增益低通滤波器，可以实现 s 平面上任意极点（实数，或者复数）位置配置。通常情况下，四个器件（R1，R2，C1，C2）取值各不相同。

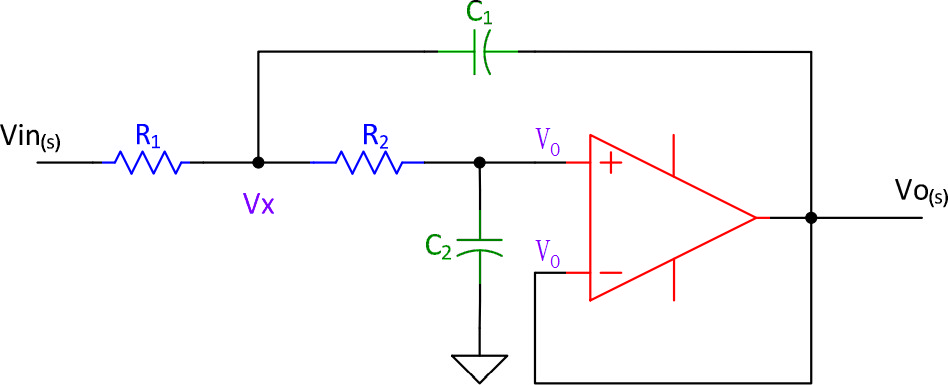
▲ 图1.2.1 Sallen-Key 单位增益低通滤波器电路

为了简化分析，考虑在 s 域分析上述电路。利用 Kirchoff 节点电流定理，流过 R1 的电流等于流过 R2，C1的电流之和。方便起见，将 R1，R2，C1 连接节点电压临时设为 Vx。利用工作在放大区域的运放“ 虚短 ”特性，可以知道运放两个输入端的电压都都与 Vo。于是有如下方程：

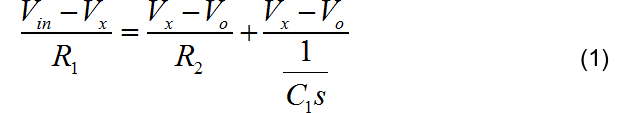
两边乘以 R1,R2消除分母，可得：

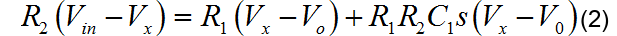
在根据 Vx，Vo之间的关系是 R2，C2 的分压关系，可以知道：

这样可以得到：

将 （4）代入（1）经过化简可以得到滤波器输入输出之间的传递函数

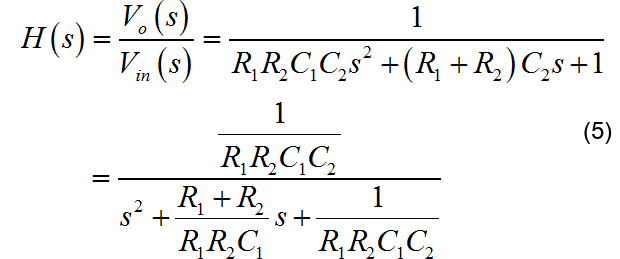
根据标准的二阶系统的形式：

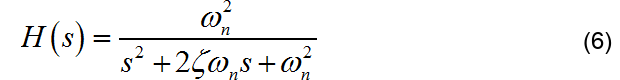
可以得到系统的自然谐振频率 和阻尼系数 ：

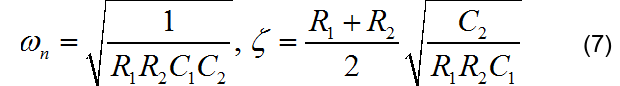
三、电路设计

电路设计是电路分析的逆过程，根据已知的两个指标（自然谐振频率和阻尼系数）设计相应的电路参数。由于未知参数是四个，所以理论上满足设计指标的滤波器参数有无穷多个。在实际电路中并不是所有的电路参数都能够很好的工作（比如电阻，电容的取值不能够太大，或者太小等），因此我们系是要确定实际可以使用的电路参数。

1、设计中的问题

2、公式推导

根据公式（7），为了方便起见，先对阻尼系数等式两边平方：

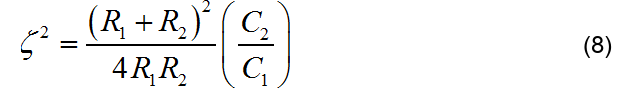
将上述公式展开，并整理成比例形式

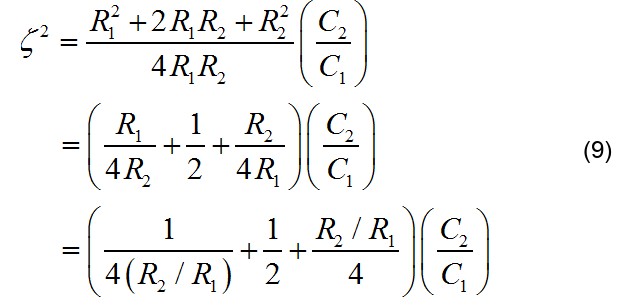
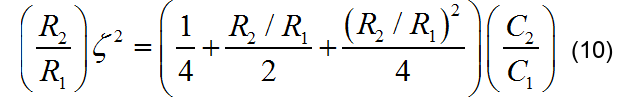
重新成立成关于比值 R2/R1 的二次方程：

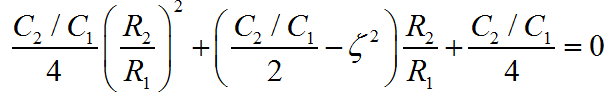
最后求解化简可得：

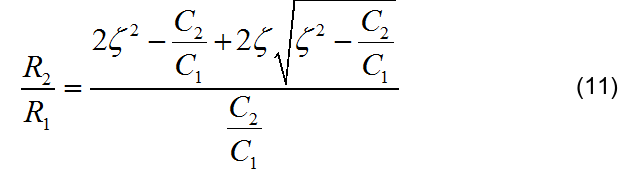
费尽万难得到公式（11），可以看出，当要求滤波器阻尼系数小于 1.0 时， 对应的电阻比值 R2/R1 就会出现复数情况，这当然在实现过程中出现困难。

3、电路设计过程

□ 步骤1：

在文档 Choosing Resisters and Capacitors for Op-Amp Active Filters ^[4]^ 给出了有源滤波器设计中电阻、电容选择标准系列。首先可以根据下面公式计算出 C1，C2 的几何平均值：

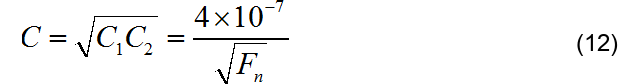
□ 步骤4：

至此，两个电容数值 C1，C2 都已经确定下来，并且是可以使用的实际电容。然后利用公式（11）计算出 R1，R2 的比值。然后在根据公式（7）的前半部分，计算出R1，R2的乘积：

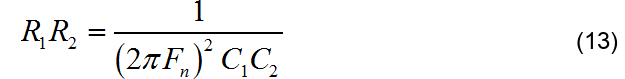
□ 步骤5：

□ 步骤6：

当设计完成之后，代入公式核算滤波器的参数（自然频率和阻尼系数）是否满足。之后再查看选择的 电容、电阻是否合理，避免过小的电容，过大的电阻，这样都可能会因为运放的偏置电流以及集成电容使得滤波器性能产生较大的偏差。

四、设计举例

下面设计一个 Sallen-Key 低通滤波器，选择自然频率为 1kHz， 滤波器的品质因素 Q=2。下面给出具体的求解过程。

五、增益变化

当运放的增益不再是标准的单位增益，会对滤波器产生什么变化吗？比如下面是通带增益大于 1 的低通滤波器。增益由 R4,R3的比值决定。

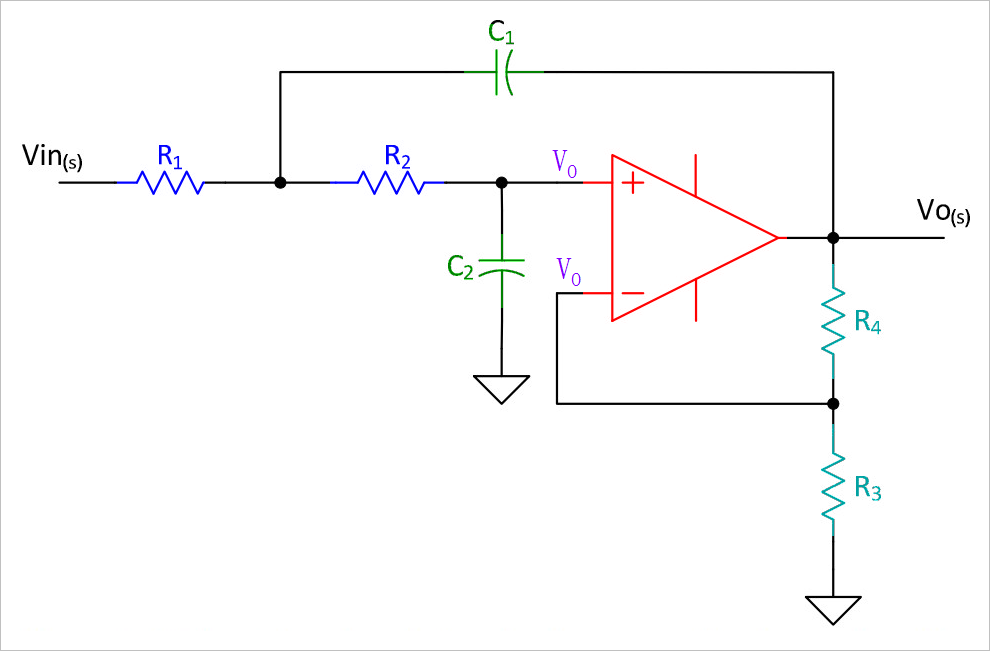
▲ 图1.5.1 通带增益大于1的Sallen-Key低通滤波器

根据同样的分析，可以得到滤波器的传递函数为：

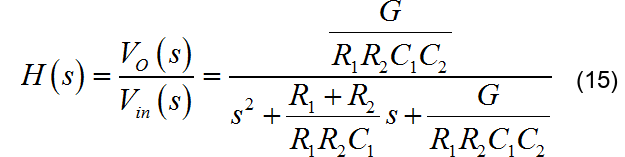
相应的滤波器参数为：

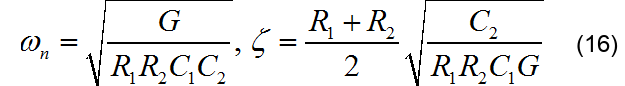
可以看到随着运放增益提高， 滤波器的自然频率增加，阻尼系数降低。如果将电容 C2 的数值。