

三相电流不对称时的绕组磁势详解
电子说
描述
前面两期分别讲了单相绕组和多相绕组产生的磁势,在前面两期的分析中,都是在绕组中通以对称正弦交流电流的前提下进行分析的。实际在电机运行时,经常会遇到三相电流不平衡、电流的波形不是完美的正弦波的情况。本期专门讲一下在三相电流不对称和电流波形不是正弦波时,绕组产生的磁势。
1 三相电流不对称时的绕组磁势
上期讲到,当对称三相绕组中通以对称三相交流电流时,三相合成磁势基波是一个幅值恒定的旋转磁势,其波幅的轨迹是一个圆,因此称为圆形旋转磁势和圆形旋转磁场。对于已经制造完成的电机,其三相绕组的匝数相等,在空间上互差120º电角度,三相阻抗相等,也就是说电机的三相绕组是完全对称的。但由于电网上存在许多单相负载和不平衡负载等情况,使得电网的三相电压可能并不能完全对称,进而使得三相电流也存在着一定程度的不平衡。那么当三相对称绕组通以三相不平衡电流时会产生什么样的磁势呢?接下来就详细分析一下这种情况。
当三相电流不对称时,可以利用对称分量法将一组不对称的三相电流IA、IB、IC进行分解,分解出三相正序分量IA+、IB+、IC+;三相负序分量IA-、IB-、IC-和三相零序分量IA0、IB0、IC0等三组对称分量,它们的有效值分别为I+、I-和I0,于是:
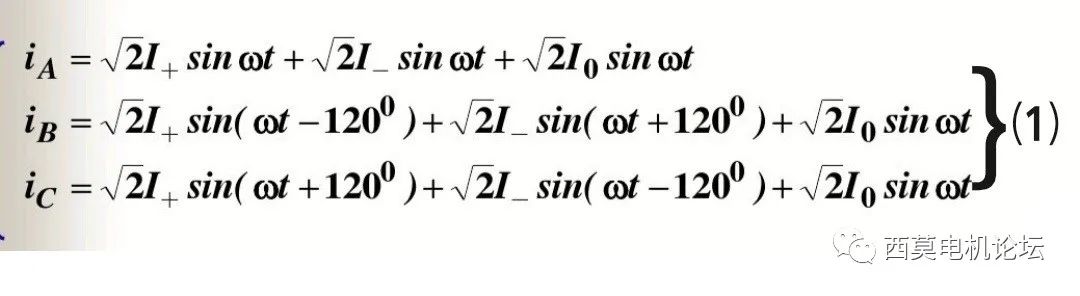 对于⑴式中的零序电流,如果三相绕组为星型接法但无中性线,则三相零序电流不存在通路,三相零序电流为0,也就不存在零序磁势;如果三相绕组为三角形接法或星型接法有中性线引出,则可能存在三相零序电流,但由于三相零序电流同相位,而三相绕组在空间上彼此相差120º电角度,因此三相零序电流产生的三个脉振磁势在时间上也是同相位,但在空间上互差120º电角度,三者合成的磁势也为0。因此无论三相绕组是何种接法,都不存在零序磁势,如式⑵、⑶所示。
对于⑴式中的零序电流,如果三相绕组为星型接法但无中性线,则三相零序电流不存在通路,三相零序电流为0,也就不存在零序磁势;如果三相绕组为三角形接法或星型接法有中性线引出,则可能存在三相零序电流,但由于三相零序电流同相位,而三相绕组在空间上彼此相差120º电角度,因此三相零序电流产生的三个脉振磁势在时间上也是同相位,但在空间上互差120º电角度,三者合成的磁势也为0。因此无论三相绕组是何种接法,都不存在零序磁势,如式⑵、⑶所示。
对于⑴式中的三相正序电流I+,它们产生的基波合成磁势为正向旋转的磁势,其幅值F1m+=1.35W•Kdp1•I+/p。
对于⑴式中的三相负序电流I-,它们产生的基波合成磁势为反向旋转的磁势,其幅值F1m-=1.35W•Kdp1•I-/p。如式⑷所示。

于是当三相绕组通以不对称的三相电流时,产生的基波磁势为一个正转的旋转磁势和一个反转的旋转磁势之和,即:
f1(t,α)=F1m+•sin(ωt-α)+F1m-•sin(ωt+α) ⑸
定义两个转向相反的旋转磁势矢量重合时的方向为X轴正方向,同时规定此瞬间作为时间的起点(t=0时刻),当经过一段时间t后,正向旋转磁势F1m+沿逆时针方向转过了ωt角度,而反向旋转磁势F1m-沿顺时针方向也转过了ωt角度,如图1所示。
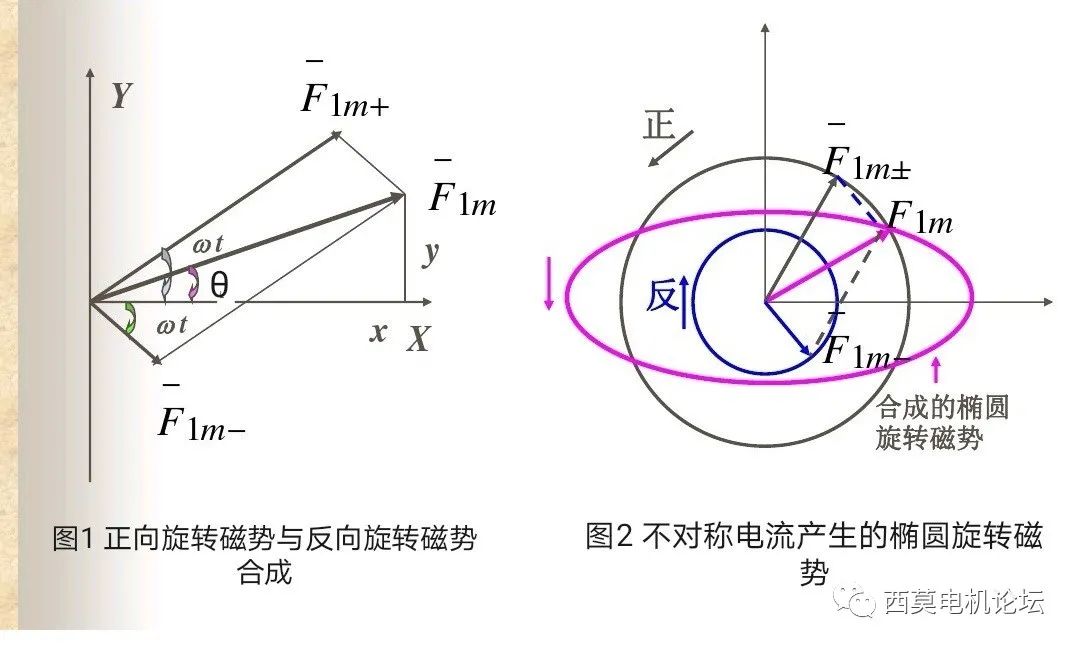 从图中不难看出,当两个磁势矢量F1m+和F1m-沿相反方向旋转时,它们的合成磁势F1m的大小和位置也随之变化。
从图中不难看出,当两个磁势矢量F1m+和F1m-沿相反方向旋转时,它们的合成磁势F1m的大小和位置也随之变化。
设F1m矢量在横轴上的投影为x,在纵轴上的投影为y,则:
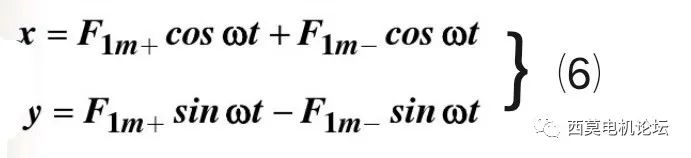 将以上两式平方后相加得:
将以上两式平方后相加得:
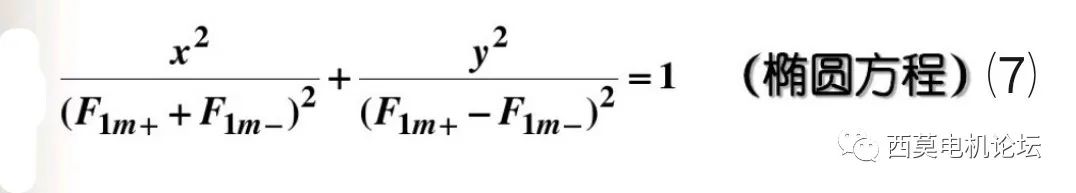 上式表明,合成磁势的端点轨迹是一个椭圆,因此也称其为椭圆旋转磁势或磁场。如图2所示。
上式表明,合成磁势的端点轨迹是一个椭圆,因此也称其为椭圆旋转磁势或磁场。如图2所示。
由图1可见,合成磁势的幅值为:
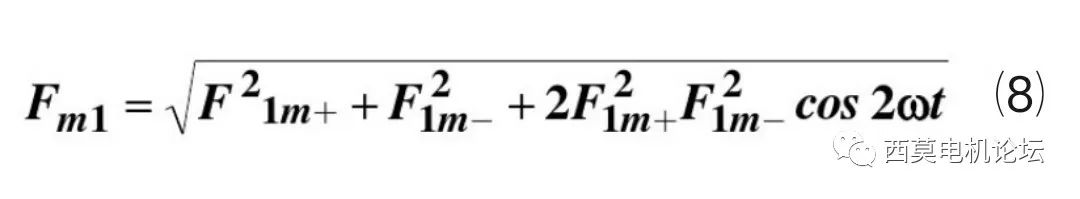 上式表明合成磁势的幅值是随时间变化的。
上式表明合成磁势的幅值是随时间变化的。
接下来分析合成磁势的旋转角速度。设合成磁势F1m与X轴的夹角为θ,则:
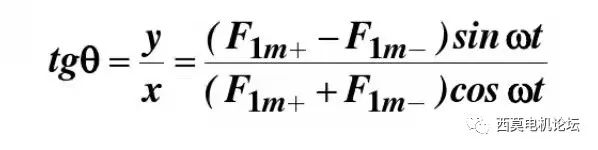 磁势的旋转角速度为:
磁势的旋转角速度为:
ω′=dθ/dt=ω•(F1m+-F1m-)/F1m² ⑼
这表明,角速度ω′与合成磁势的平方成反比,故在椭圆的长轴附近角速度较低,在椭圆的短轴附近角速度较高,因此角速度不是常数。至于合成磁势的旋转方向,取决于正向旋转的磁势和反向旋转的磁势哪一个更强。
式⑸是交流绕组磁势的普遍表达式。当正向旋转磁势F1m+和反向旋转磁势F1m-中任意一个为0时,即是圆形旋转磁势;当F1m+=F1m-时,便是脉振磁势;当F1m+和F1m-都存在且大小不相等时,便是椭圆旋转磁势,转向与较大的磁势转向相同。
2 非正弦电流下的绕组磁势
若通入三相绕组的电流为非正弦电流,则可以利用傅立叶分解把三相电流分解为基波和一系列谐波。必须反复强调指出的是,三相电流是时间的函数,因此这种傅立叶分解是在时间上的分解,也就是说,把随时间作非正弦变化的三相电流分解成一系列随时间以不同频率做正弦变化的三相电流。这样三相的每个次数的谐波电流都相当于一个对称的三相电流,只不过不同次数的谐波电流随时间变化的频率不同而已。任意一个三相谐波电流都会在气隙中产生一系列的空间谐波磁势,注意!磁势波是空间波!即使是三相绕组中通入的是直流电流,也会在气隙中产生一系列的空间谐波磁势,只不过直流电流产生的一系列谐波磁势是幅值恒定且静止的磁势,而不同次数的谐波电流产生的磁势是幅值恒定的旋转磁势,其转速取决于谐波电流的频率,转向则取决于谐波电流的相序。
2.1 三相电流的傅立叶分解
将三相对称的非正弦电流进行傅立叶分解后,不存在直流电流分量和三次以及三的整数倍次谐波分量。则三相电流傅立叶分解后为:
iA=I1m•sin(ωt+φ1)
+I5m•sin(5ωt+φ5)
+I7m•sin(7ωt+φ7)
+…
=∑Iμm•sin(μ•ωt+φμ)
iB=I1m•sin(ωt-120º+φ1)
+I5m•sin[5(ωt-120º)+φ5]
+I7m•sin[7(ωt-120º)+φ7]
+…
=∑Iμm•sin[μ(ωt-120º)+φμ]
iC=I1m•sin(ωt-240º+φ1)
+I5m•sin[5(ωt-240º)+φ5]
+I7m•sin[7(ωt-240º)+φ7]
+…
=∑Iμm•sin[μ(ωt-240º)+φμ] ⑽ 式中:μ=6k±1。
2.2 各次谐波电流产生的磁势
上篇文章已经详细讲述了三相基波电流产生的磁势。简要回顾一下:基波电流除了产生(空间)基波磁势外,还产生各次(空间)谐波磁势。其中基波磁势是一个幅值恒定的圆形旋转磁势,其转速为ns=60f/p(r/min),由于基波的相序为A—B—C—A…,因此将其旋转方向定义为正方向。基波电流产生的谐波磁势也是一系列的圆形旋转磁势,其转速为ns/υ(υ为磁势空间谐波次数),即同步转速的1/υ倍,谐波次数越高,转速越低。基波电流产生的谐波磁势转向为:当υ=6k-1(k=1,2,3…)时为反向旋转(与基波磁势转向相同);当υ=6k+1(k=1,2,3…)时为正向旋转。
再看5次(时间)谐波电流产生的磁势。5次谐波电流也是一个对称的三相电流,只不过电流的变化频率为基波频率的5倍。5次(时间)谐波电流同样会产生(空间)基波磁势和谐波磁势。由于5次谐波电流的频率是基波频率的5倍,因此5次(时间)谐波电流产生的(空间)基波磁势的转速为5ns,即5倍同步转速。而5次(时间)谐波电流产生的(空间)基波磁势的旋转方向要看5次谐波电流的相序。那么5次谐波电流的相序是什么呢?从⑽式中可以看出,三相5次谐波电流为:
iA5=I5m•sin(5ωt+φ5)
iB5=I5m•sin[5(ωt-120º)+φ5]
=I5m•sin(5ωt+120º+φ5)
iC5=I5m•sin[5(ωt-240º)+φ5]
=I5m•sin(5ωt+240º+φ5) (11)
由(11)式可见,5次谐波电流的相序是A—C—B—A…,即5次谐波电流的相序与基波电流相序相反,为逆相序。这是许多同学经常犯错误或不注意的地方!在仿真5次谐波电流产生的转矩脉动时,输入的5次谐波电流相序经常是错误。画重点再重复一遍:5次谐波电流的相序与基波电流相序相反,为逆相序!因此五次谐波电流产生的基波磁势为反向旋转磁势!转速为同步转速的5倍!
说完5次谐波电流产生的基波磁势,再说5次谐波电流产生的5次谐波磁势。正序电流产生的5次谐波磁势为反转磁势,那么负序电流产生的5次谐波磁势就为正转磁势,因此负序的5次谐波电流产生的5次谐波磁势就应该是正转磁势。其转速为μ•ns/υ,其中μ=5,υ=5,因此5次谐波电流产生的5次谐波磁势转速为同步转速。
按照上述同样的分析方法,可以得出5次谐波电流产生的7次谐波磁势为正向旋转磁势,转速为(5/7)ns;5次谐波电流产生的11次谐波磁势为反向旋转磁势,转速为(5/11)ns;余类推(不再赘述)。
同理,7次谐波电流为正相序,产生的基波磁势为正向旋转磁势,转速为同步转速的7倍;7次谐波电流产生的5次谐波磁势为反向旋转磁势,转速为(7/5)ns;7次谐波电流产生的7次谐波磁势为正向旋转磁势,转速为同步转速;7次谐波电流产生的11次谐波磁势为反向旋转磁势,转速为(7/11)ns;余类推…
归纳一下:μ次谐波电流产生的υ次谐波磁势为:
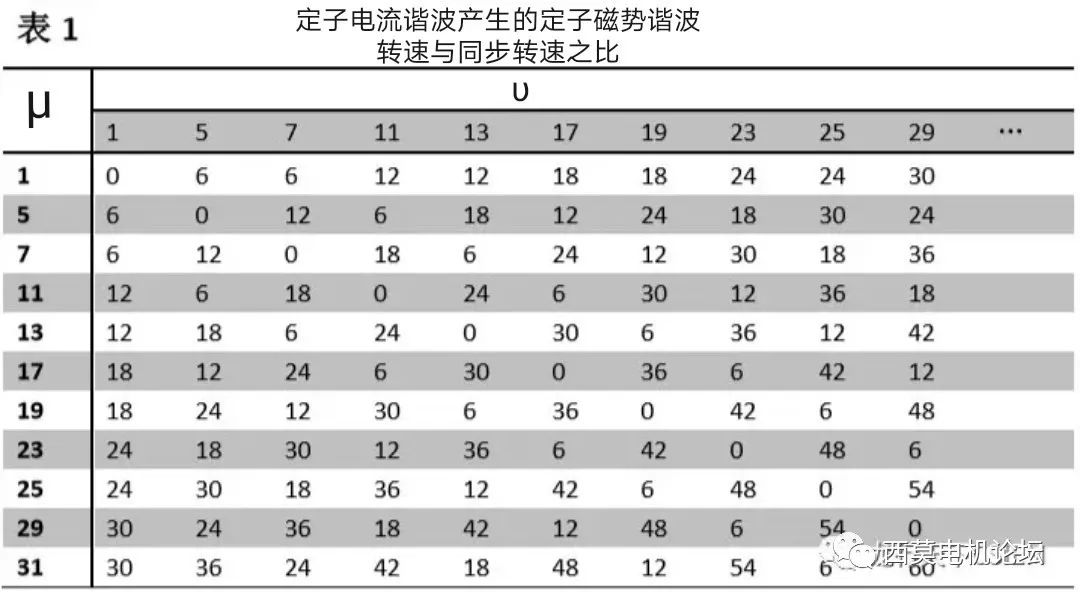
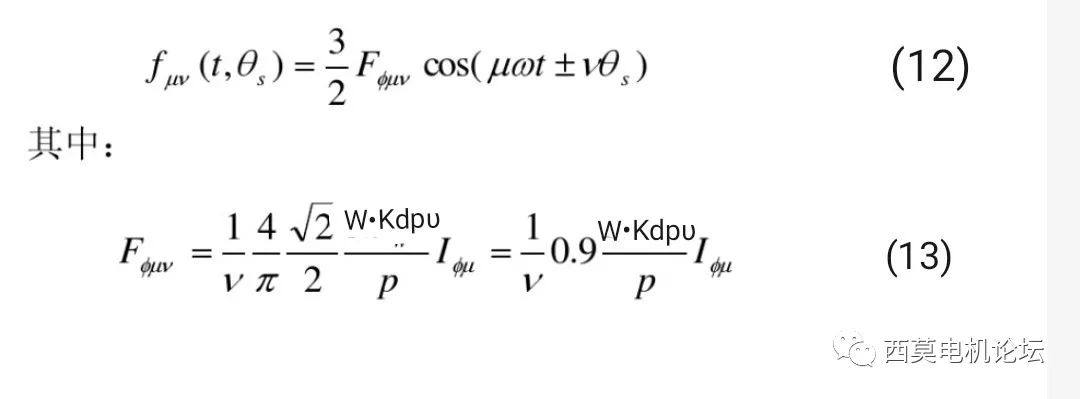 式(12)中μ=6k±1;υ=6k±1。当μ和υ中的“±”号取同号时,(12)式中的“±”号取“-”号,表明转向为正转向;当μ和υ中的“±”号取异号时,(12)式中的“±”号取“+”号,表明转向为反转向。μ次谐波电流产生的υ次谐波磁势的转速为(μ/υ)•ns,当转子以同步转速正向旋转时,这些谐波磁势的转速相对于转子的转速之比见表1。
式(12)中μ=6k±1;υ=6k±1。当μ和υ中的“±”号取同号时,(12)式中的“±”号取“-”号,表明转向为正转向;当μ和υ中的“±”号取异号时,(12)式中的“±”号取“+”号,表明转向为反转向。μ次谐波电流产生的υ次谐波磁势的转速为(μ/υ)•ns,当转子以同步转速正向旋转时,这些谐波磁势的转速相对于转子的转速之比见表1。
 说到这里,必须提醒一下,前面讲的都是定子绕组产生的磁势(简称定子磁势),不是转子磁势。定子磁势的转速取决于定子电流频率和谐波次数,当定子电流频率一定时,定子谐波磁势的次数不同,转速和转向也不尽相同。有些谐波正转有些谐波反转。而对于同步电机,转子磁势也包括基波和一系列谐波,与定子磁势不同的是,转子各次谐波磁势的转速和转向都与转子的机械转速和转向相同。我们知道,要想实现稳定的机电能量转换,必须定转子磁场的极对数相同,且定转子磁场保持相对静止,即定转子磁场极对数相同、转向相同、转速相同。
说到这里,必须提醒一下,前面讲的都是定子绕组产生的磁势(简称定子磁势),不是转子磁势。定子磁势的转速取决于定子电流频率和谐波次数,当定子电流频率一定时,定子谐波磁势的次数不同,转速和转向也不尽相同。有些谐波正转有些谐波反转。而对于同步电机,转子磁势也包括基波和一系列谐波,与定子磁势不同的是,转子各次谐波磁势的转速和转向都与转子的机械转速和转向相同。我们知道,要想实现稳定的机电能量转换,必须定转子磁场的极对数相同,且定转子磁场保持相对静止,即定转子磁场极对数相同、转向相同、转速相同。
前面的分析可知,基波电流产生的基波磁势的转速为同步转速,与转子基波磁势的极对数相同、转速相同、转向相同,因此基波电流产生的基波磁势与转子基波磁势相互作用产生恒定的转矩,这是同步电机(乃至任何电机)实现机电能量转换的基础。除此之外,5次谐波电流产生的5次谐波定子磁势转速也是同步转速,转向也是正向旋转,与转子5次谐波磁势同样是极对数相同、转速相同、转向也相同,因此它们相互作用同样产生恒定转矩。同理当定子电流的谐波次数与所产生的定子磁势谐波次数相同时,都与转子同次谐波磁势极对数相同并保持相对静止,它们相互作用都会产生恒定转矩,实现稳定的机电能量转换。从这个意义上讲,并不是所有的谐波磁势都是有害的,那些与电流的时间谐波次数相等的谐波磁势,对于机电能量转换来讲是有益的。这就是方波供电的无刷直流电机可以实现稳定机电能量转换的基础。除了这些特定的谐波外,其他谐波磁势,要么与转子磁势极对数不同,不产生转矩;要么就是极对数相同,但转速或转向不同,产生脉动转矩,这对电机的运行是有害的。
本期分析了定子三相电流不平衡和定子电流非正弦时产生的定子磁势。下期讲定子谐波磁势产生的原因,即所谓的“相带谐波”和“齿谐波”,敬请期待!
审核编辑:汤梓红
-
OPA2365用作三相下桥臂电流检测,测得的电流波形不对称是为什么?2024-08-09 384
-
分析三相绕组的合成磁势2023-10-09 6925
-
为什么三相对称绕组中经过三相对称电流会产生圆形磁场呢?2023-03-06 1743
-
浅谈三相绕组磁势及其合成磁势基波2018-10-23 3083
-
基于三相PFC整流器在输入电压不对称时的问题分析2018-10-10 2986
-
采用不对称绕组变压器的不对称半桥电路的研究及原理2017-09-14 1333
-
电路设计--不对称三相电路的概念2017-08-25 1992
-
三相PFC整流器在输入电压不对称时的改进2012-02-21 5534
-
Y—Y0不对称三相电路故障分析2010-05-12 1864
-
采用不对称绕组变压器的不对称半桥电路的研究2009-10-19 1230
-
不对称三相电路2009-07-27 7627
-
三相不对称负载下对不对称与无功功率综合补偿方法2009-04-03 1200
-
三相电路-相序、电流、电压及功率的测量2008-12-17 28757
-
不对称三相电路计算2008-09-24 3618
全部0条评论

快来发表一下你的评论吧 !

