从谐振器到滤波器，简述SAW滤波器的设计过程

今天我们继续分享一篇关于声波滤波器的文章《RF filter design – from resonators to filters》，文章作者是 Gergely Simon，最初发表在onscale.com的blog。【射频学堂】翻译整理，分享大家学习参阅。

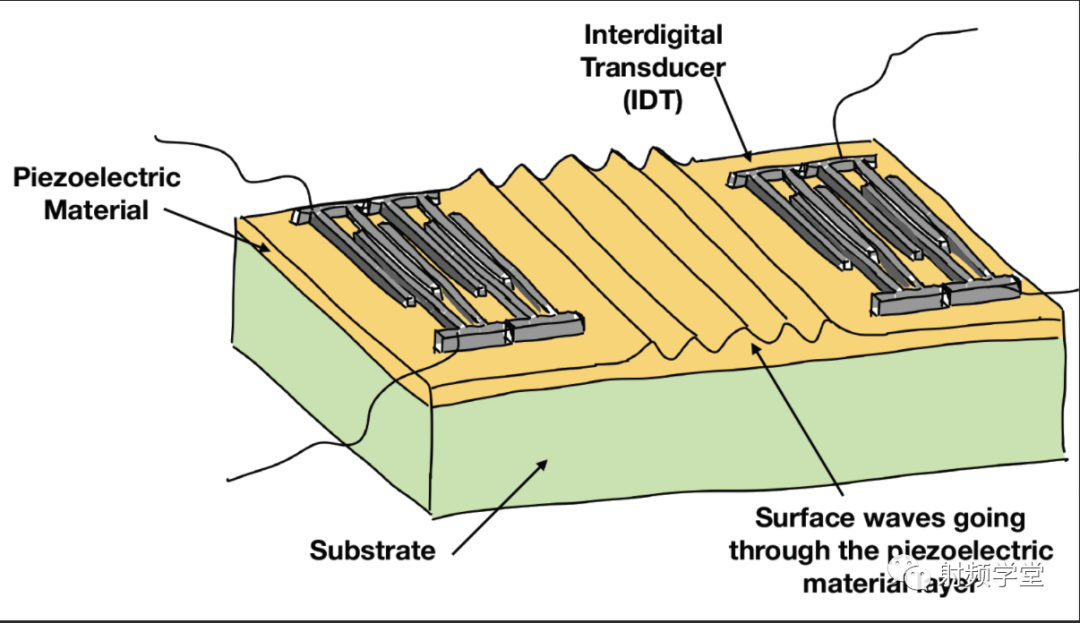
为什么我们需要滤波器？

随着移动设备之间数据传输和通信需求的增加，尤其是所需带宽的增加，越来越多的频段被用于移动数据（2G 到 5G）、WiFi 甚至简单的电话通话。这些需要彼此适当隔离，以避免串扰和不需要的噪声信号。为了实现这一点，使用了滤波器：它们只允许某些频率通过，并且根据这些频率的范围，可以分为低通、高通、带通和带阻。

我们想要达到什么目标？

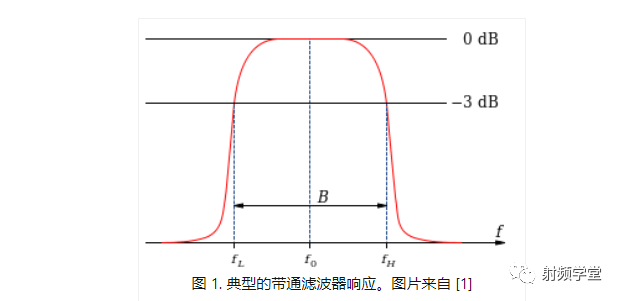
为简单起见，在这篇博文中，我们将介绍带通滤波器：它们允许两个频率之间的大部分能量通过滤波器，同时阻止超出此范围的任何内容（见图 1）。真正的设备从来都不是完美的：插入损耗表示带内信号的不完美通过，而抑制则量化了带外通过的信号量。这些以分贝 (dB) 表示，插入损耗小于 -3 dB，抑制至少 30 dB 被认为是足够的滤波器行为。

我们如何实现它？

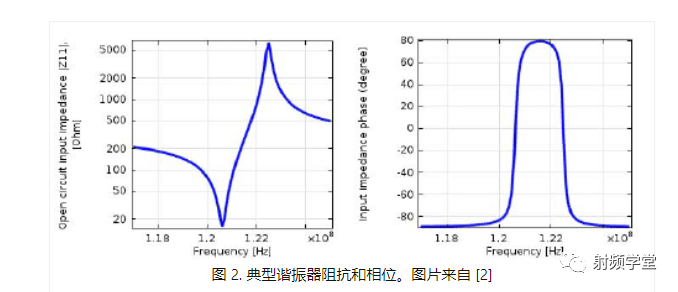
在滤波器中，通常使用谐振器，其典型阻抗响应如图 2 所示。

它们以各种拓扑级联，最终以尽可能高的选择性实现整体带通行为。在最简单的情况下，采用所谓的梯形拓扑，如图 3 所示。

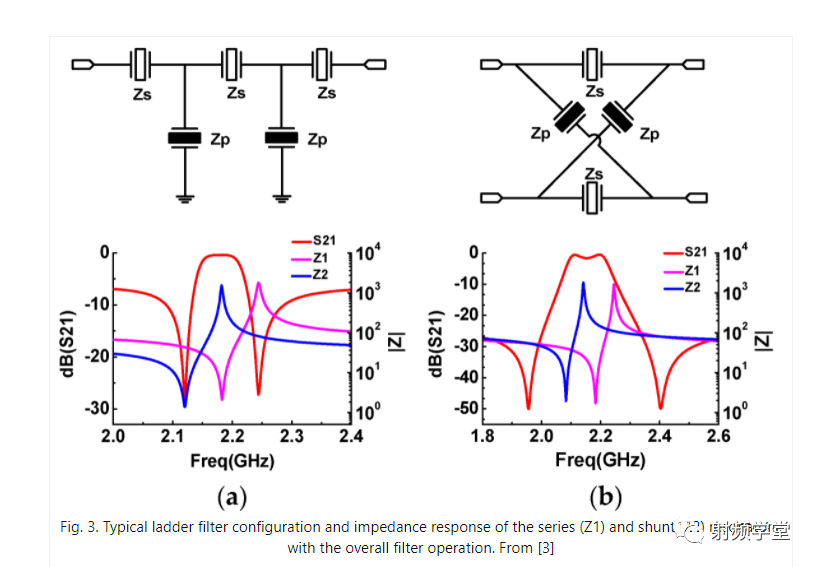
让我们详细看一下这个例子。请注意，串联谐振器（图 3 中的洋红色曲线）比并联谐振器（图 3 中的蓝色曲线）具有更高的频率响应，并且并联谐振器的并联谐振频率与串联谐振器的串联谐振频率对齐（品红色曲线相对于蓝色曲线向右移动）。

现在，如果我们考虑只有一个级的设置（图 3 顶部的一个 Zs 和一个 Zp），可以提出以下论点，想象这基本上是一个分压器：

带外（~2.1 GHz 左侧和~2.25 GHz 右侧）两个谐振器的阻抗相当——输出大约是输入的一半

在并联谐振器的串联谐振频率附近（下截止，~2.1 GHz），并联谐振器的阻抗变为零，实际上将输出接地，显着降低信号

在分频器 (~2.2 GHz) 附近，并联谐振器的阻抗趋于显着增加，而串联谐振器的阻抗趋向于零——这在输入和输出之间几乎造成短路，同时通过几乎理想的接地隔离开路。

在上截止频率 (~2.25 GHz) 附近，第 2 点发生相反的情况：串联阻抗趋于无穷大，将输出与输入隔离，并且透射率再次急剧下降

此外，并联谐振器的阻抗通常低于串联谐振器的阻抗（红色曲线相对于蓝色曲线向上移动）。这进一步增加了带外抑制，因为输出端的分压值始终较小（考虑带外）。

最后，请注意，通常使用传输线理论和传播波携带的功率来研究这些滤波器。尽管如此，分压器类比提供了一个很好的定性概述。

其他拓扑

梯形滤波器没有很大的带外抑制，如图 4 所示。因此，可以采用其他拓扑结构，例如格结构或组合梯格拓扑（图 5）。

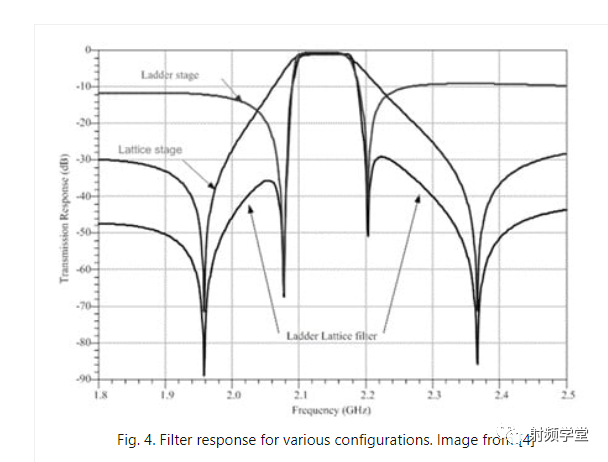
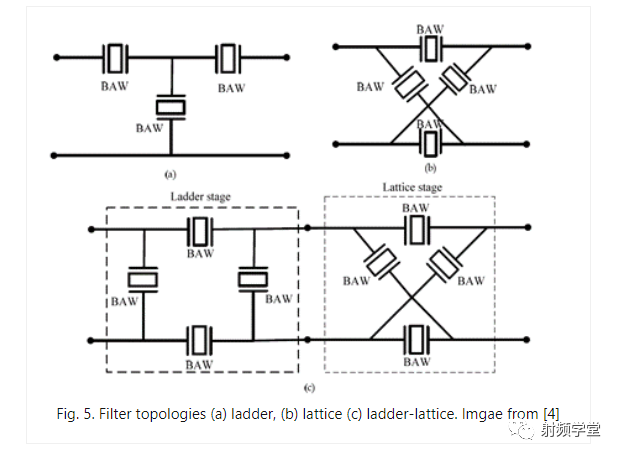
有关结构和设计注意事项的更多信息，请参见参考资料和 Ken-ya Hashimoto：RF Bulk Acoustic Wave Filters for Communications。