

介绍电阻并联的一般情况
电子说
描述
“并联”一词通常用来描述两个元件之间的一种物理连接关系,这些元件的特性通常是已知的。一般地,如果两个元件,或两个支路,或两个电路,它们有两个公共的连接点.就称它们为并联连接,简称并联。
例如,图1a中的两个电阻是并联,因为它们存在两个公共的连接点a和b,在图1b中,电阻R1和R3也是并联,因为它们也有两个公共的连接点a和b;而R1和R3不是并联,因为它们只有一个公共点b;同理,R2和R3也不是并联。
在图1c 中,R1和R2是串联,因为它们仅含有一个公共点,并且这个点没有与电路的其他部分连接;电阻R1和R3不是并联,因为它们仅有一个公共点a;另外,它们也不是串联,因为还有第三条支路连接到a点;同理可以说明R2和R 3, 它们既不是串联,也不是并联。
在更广泛的意义下,可以说是R1和R2的串联支路与R3并联。进一步地,尽管以上讨论只是针对电阻的情形,但同样适用于任何二端元件,例如电压源和各种测量仪表。
在绘制电路图时,表示并联的连接有多种,如图1所示。在每一种情况下,三个电阻都是并联的,因为它们都有公共点a和b。
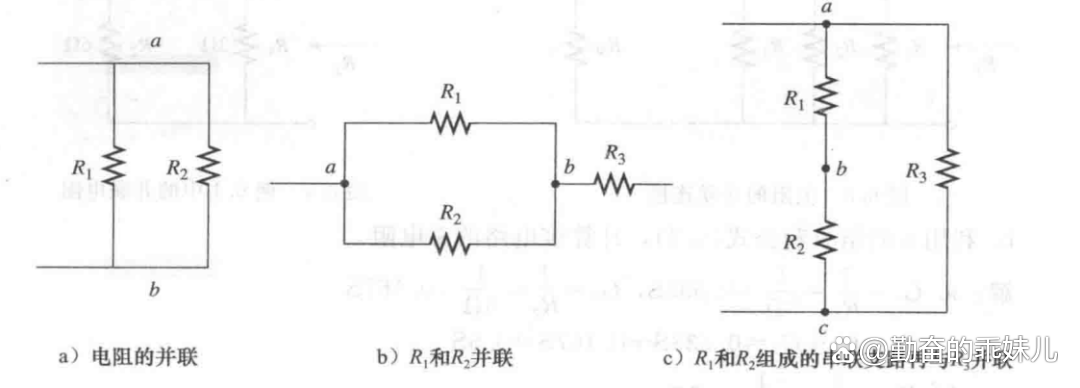
图 1:三个电阻并联的电路图
对于如图2所示的并联电路,总电阻由下面公式决定:
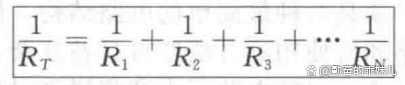
(1)
由于G=1/R,因此上式也可写成电导的形式,为:
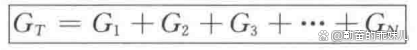
(2)
这与电阻串联的总电阻公式在形式上是一致的,即R T =R 1 +R 2 +R 3 +...十R N 。这种对偶关系,可以让你轻松地从一个公式得到另一个公式,只需简单地交换R和G。
当需要计算总电阻值时,则需要应用如下形式的公式:

(3)
很显然,公式(3)不像串联电路总电阻公式那样简捷,你必须小心计算所有倒数这个公式的主要特点是,它可以用来计算任何数量电阻并联后的总电阻。

图2:电阻的并联连接
例1.
a.计算图3中并联电路的总电导
b.利用a的结果和公式(3),计算该电路的总电阻。
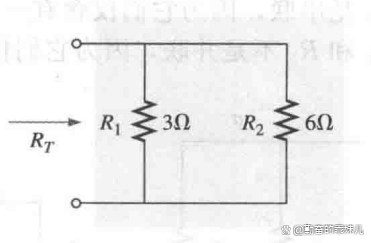
图3
解:


应用公式(3)得

例2.
a.观察图4中哪一个并联元件具有最小的电导值?确定网络的总电导,并说明你的结论是否得到证实。
b.利用a的结果和公式(3)确定总电阻值。

图4
解:
a.由于在所有并联电阻中1kΩ电阻为最大,因此它对电流的阻碍作用也最大即它具有最小的电导值。
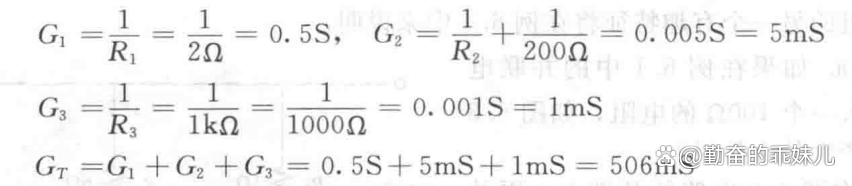
注意2Ω(500mS)和1kΩ(1mS)电阻对应电导值的差别。
b.
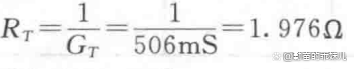
应用公式(3)得:

-
运放测量输入偏置电流和输出电阻一般电路是怎么搭的呢?2023-11-22 631
-
电路设计--电阻电路的一般分析2017-02-28 1182
-
关于AD的一般性介绍2017-10-18 894
-
关于AD的工具一般性介绍2017-11-01 825
-
电阻串联和并联的计算方法_电阻串联和并联的作用2018-01-21 219098
-
串联电阻和并联电阻的计算方法2019-06-24 114394
-
人体电阻是多少_人体电阻值一般是多少2019-09-18 231188
-
并联电阻的特点是什么_并联电阻故障处理2019-09-26 21202
-
精密电阻和一般电阻的区别2020-08-02 6002
-
电阻电路的一般分析复习题和答案免费下载2020-09-28 1164
-
电阻电路的等效变换及一般分析2022-03-24 926
-
介绍一般人不知道的三种特殊电阻器2022-07-05 2513
-
中性点接地电阻柜一般是多大尺寸的2022-12-13 841
-
ESD与一般电压保护压敏电阻的区别2023-06-30 2390
-
压敏电阻一般有什么选用原则与选项举例?2023-10-30 3099
全部0条评论

快来发表一下你的评论吧 !

