

永磁轮毂电机有限元计算 永磁轮毂电机性能的优化
电子说
描述
本文针对机场摆渡车,设计一台额定功率60 kW,额定转矩2 500 N·m的外转子表贴式永磁轮毂电机,较好地满足机场摆渡车运行速度低、运行稳定性高的特点。首先给出电机的基本参数尺寸,其次利用有限元软件计算了电机的空载特性和负载特性,最后分析永磁体斜极对电机齿槽转矩、反电动势和电磁转矩的影响,综合得出电机最优尺寸。
1 永磁轮毂电机主要尺寸
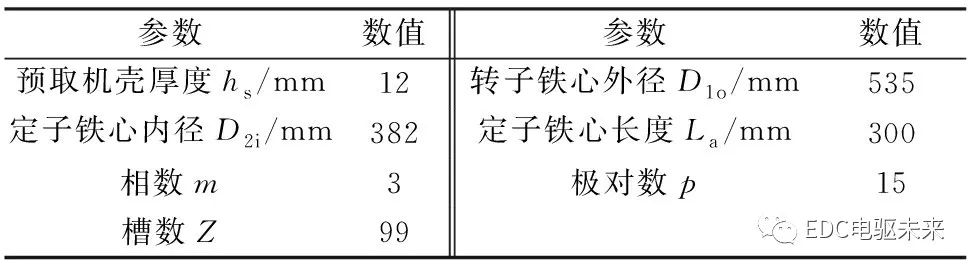
机场摆渡车用轮毂电机需要在高温下运行,通常定子绕组温度能达到200 ℃,转子外壳温度可达160 ℃。同时电机在转速较低情况下要提供较大转矩,并且要有较强过载能力,因此电机选择直接将转子安装在车圈上的外转子表贴式结构。综合考虑电机在机场摆渡车车轮中的应用,基本电机尺寸如表1所示。
表1 电机主要尺寸
2 永磁轮毂电机有限元计算
2.1 空载特性分析
图1为空载时磁密云图,时间为一个电周期。电机整体结构没有出现严重饱和部分,只有定子齿尖有一定的饱和现象,齿尖少数部分的饱和对电机性能影响较小。图2为气隙的径向磁密波形。磁密波形近似于方波,磁密最大达到0.81 T。在模型中,以圆心到定子齿长和定子轭厚度的一半为半径分别建立路径,得到定子齿部与定子轭部的磁密,如图3和图4所示。从图3、图4中可以看出,定子齿部磁密最大值达到1.32 T,定子轭部磁密最大值为0.96 T,基本满足设计要求。
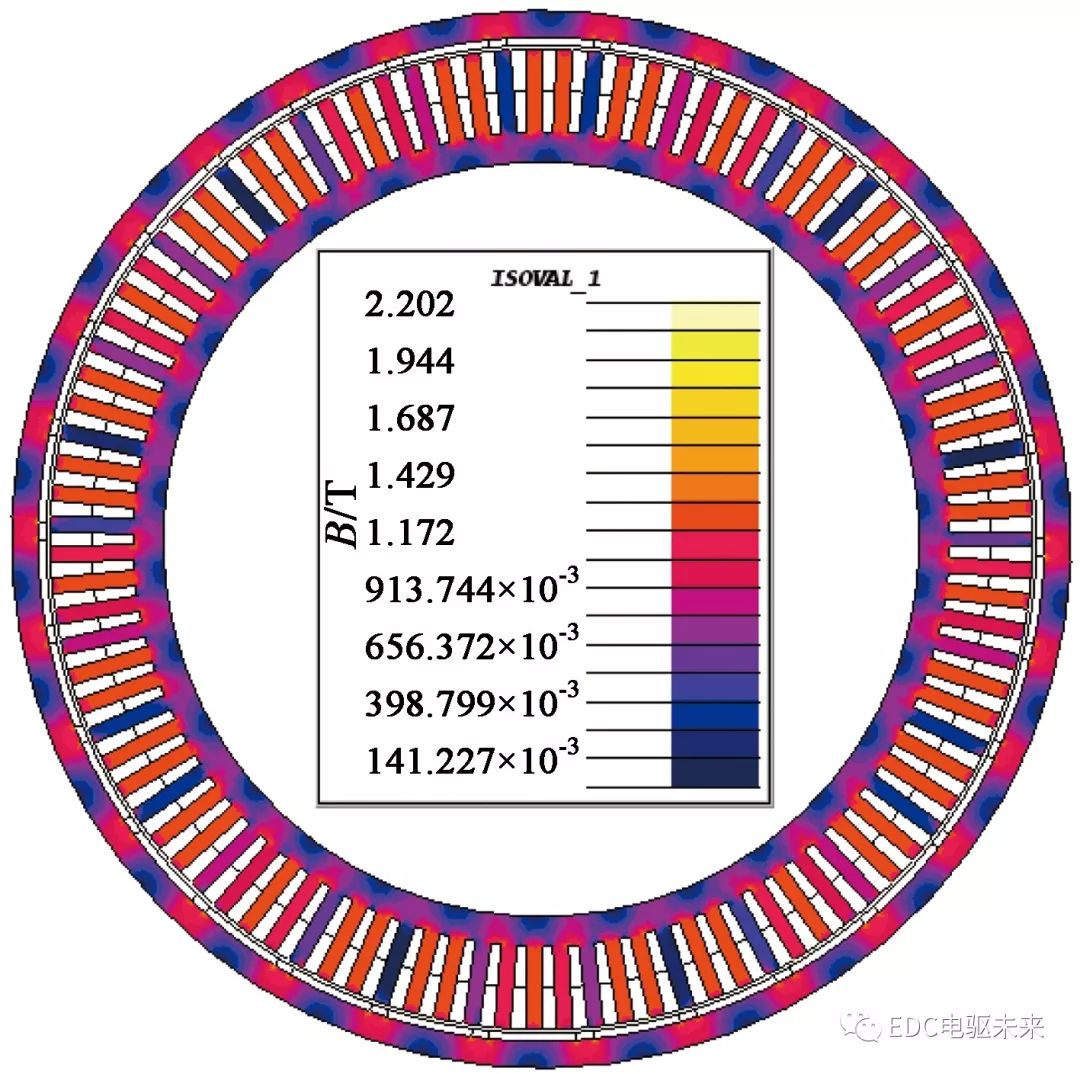
图1 空载特性下的磁密云图
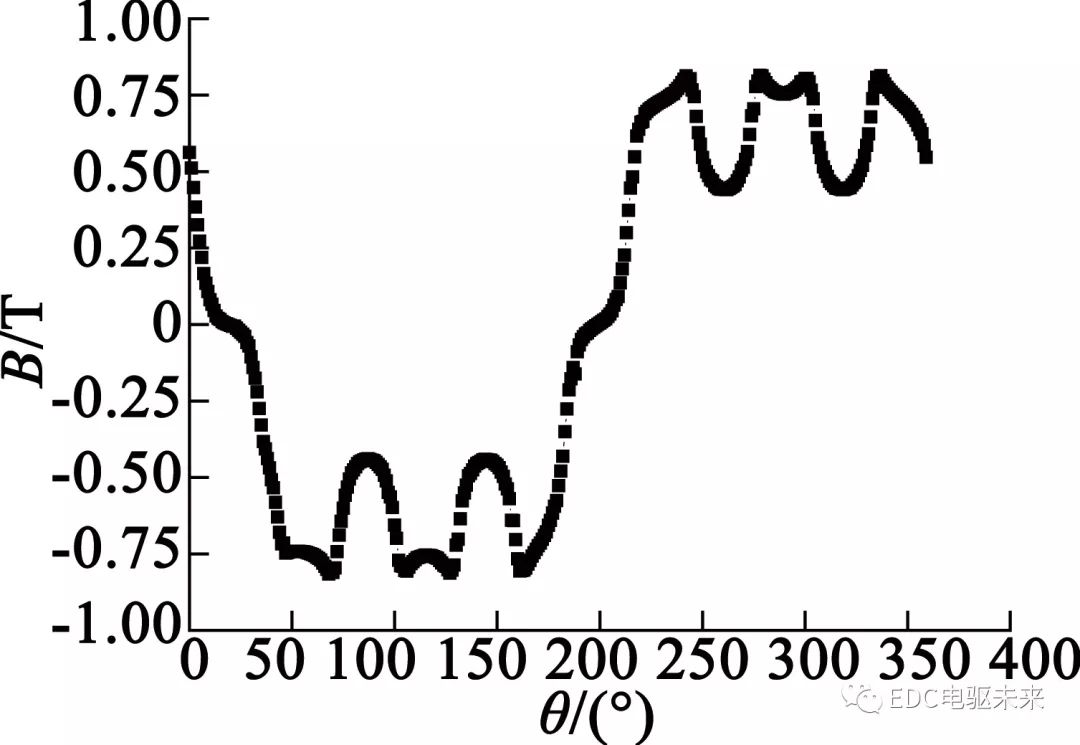
图2 气隙磁密波形
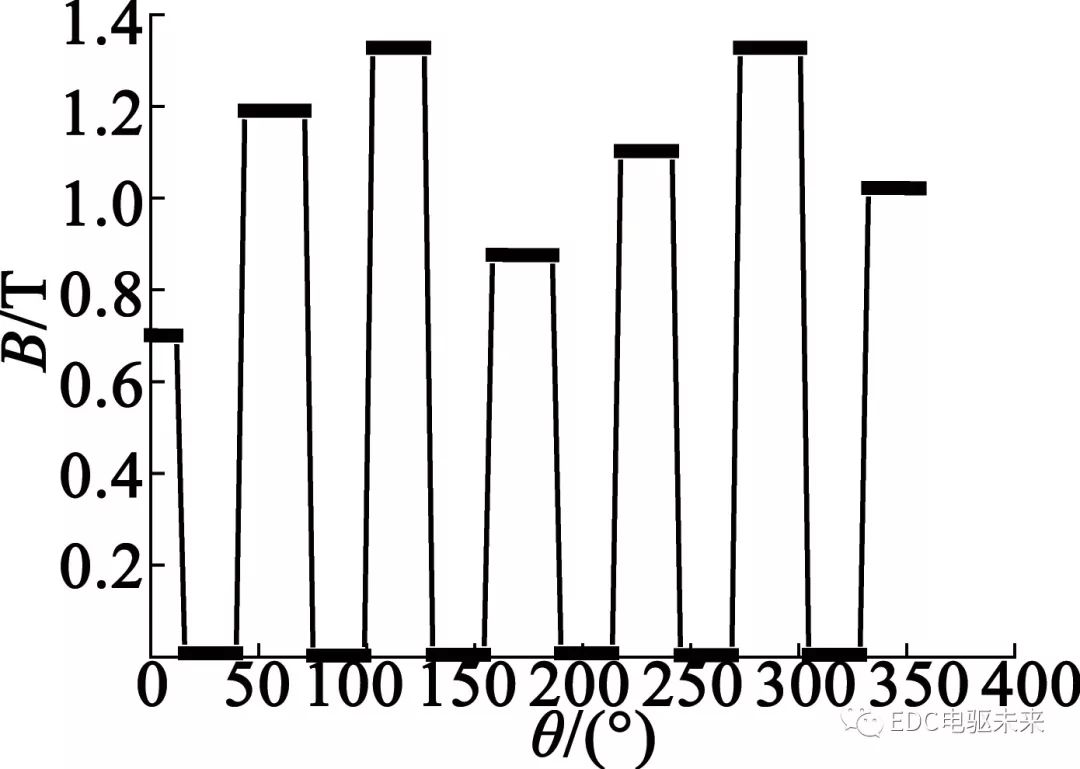
图3 定子齿部磁密图
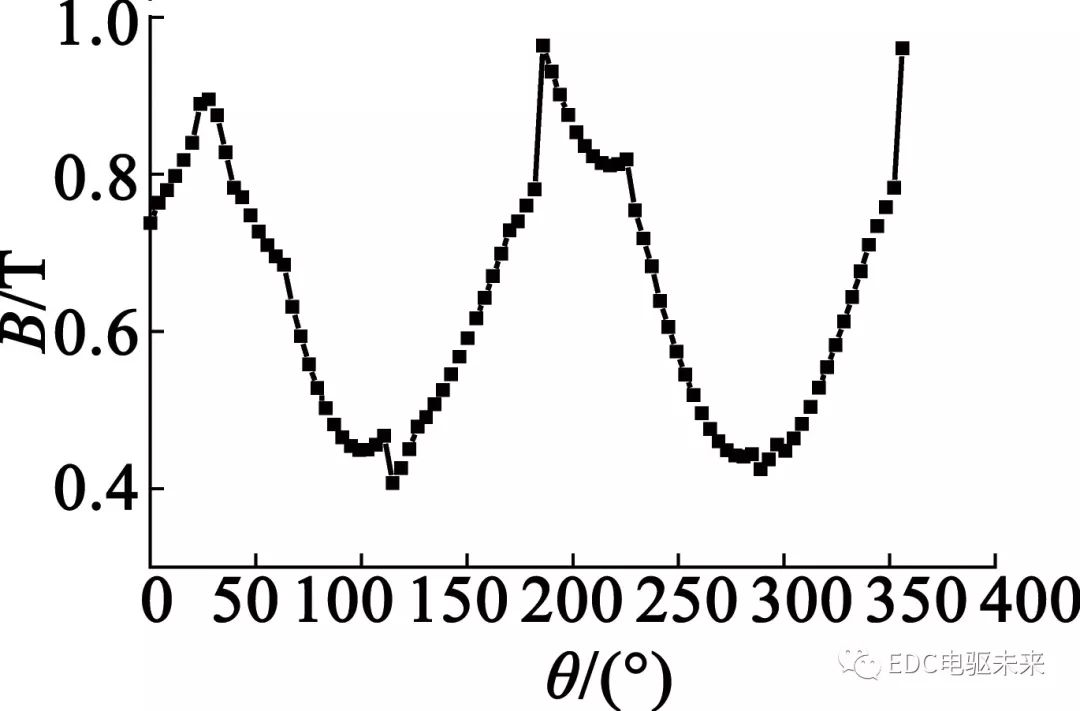
图4 定子轭部磁密图
图5给出了空载条件下的三相绕组线电动势波形,线电动势幅值在280 V左右。图6给出了齿槽转矩波形图,从图6中可以看出,一个电周期的波动次数为66次,波动幅值为0.45 N·m,波动幅值较小。
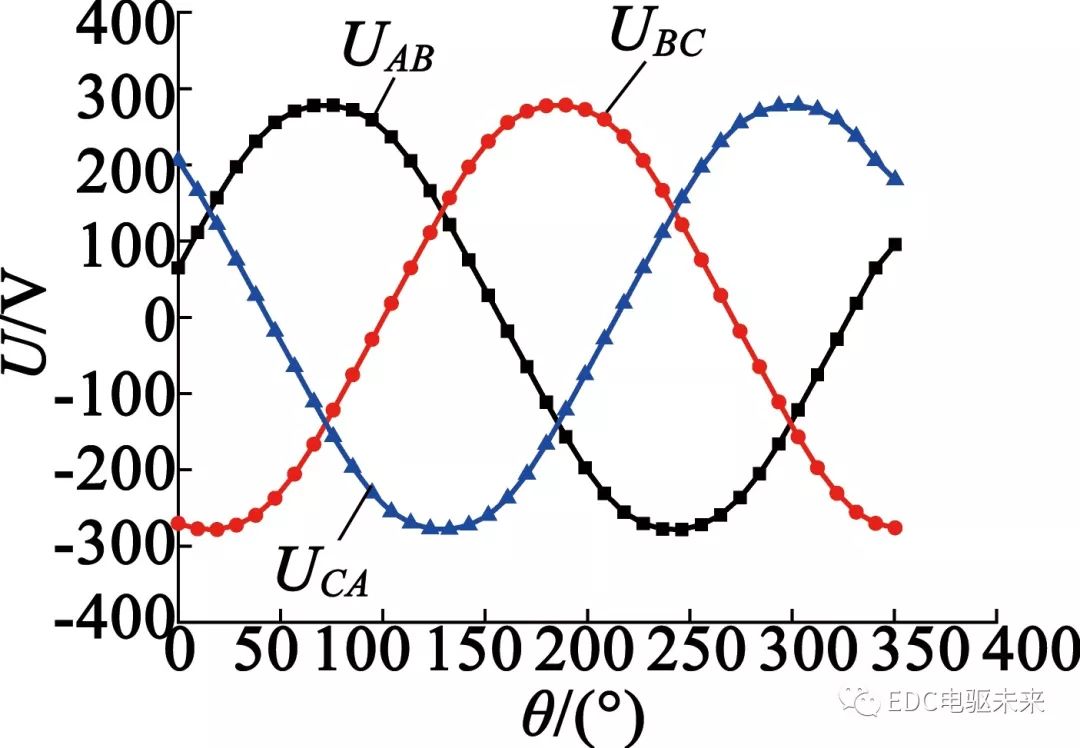
图5 空载线电动势波形
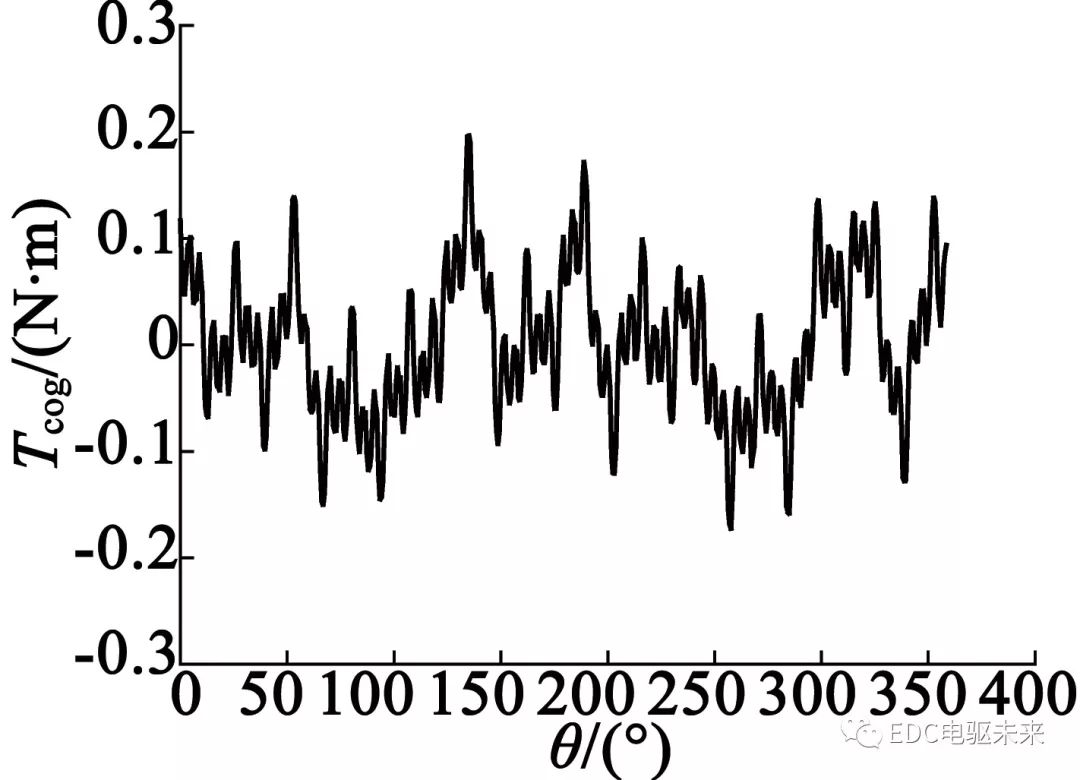
图6 齿槽转矩波形图
2.2 负载特性分析
定子绕组通入180 A电流时,电磁转矩波形如图7所示。电磁转矩波动幅值为76 N·m,波动幅度较大,同时平均转矩达到额定转矩2 500 N·m, 电机各部分除齿尖外没有出现饱和。图8给出此时的线电动势波形,可得线电动势幅值达到335 V。
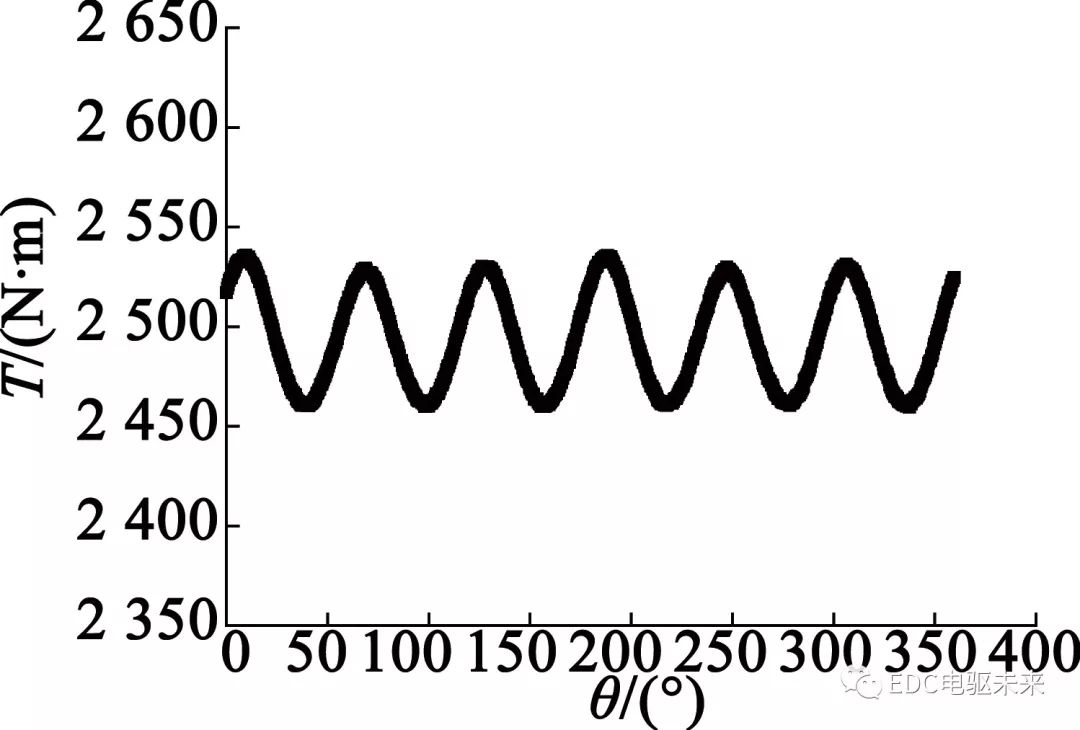
图7 额定转矩波形
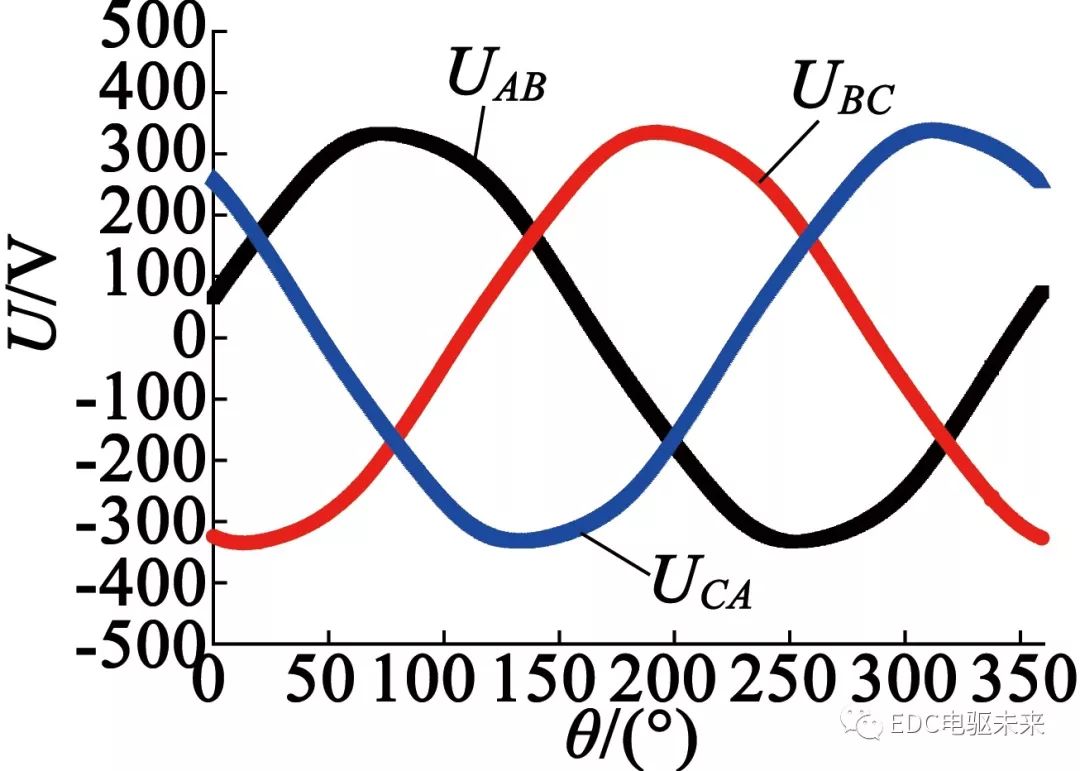
图8 三相感应电动势波形
当定子绕组通入425 A电流,得到此时电磁转矩波形,如图9所示,此时达到最大输出转矩5 250 N·m,波动幅值达到170 N·m,波动幅值较大。图10为通入425 A电流的线电动势波形,幅值接近410 V,没有超过最大电压。图11为电磁转矩平均值随电流变化曲线。从图11中可以看出,随着电流的增大,电磁转矩近似呈线性增长。
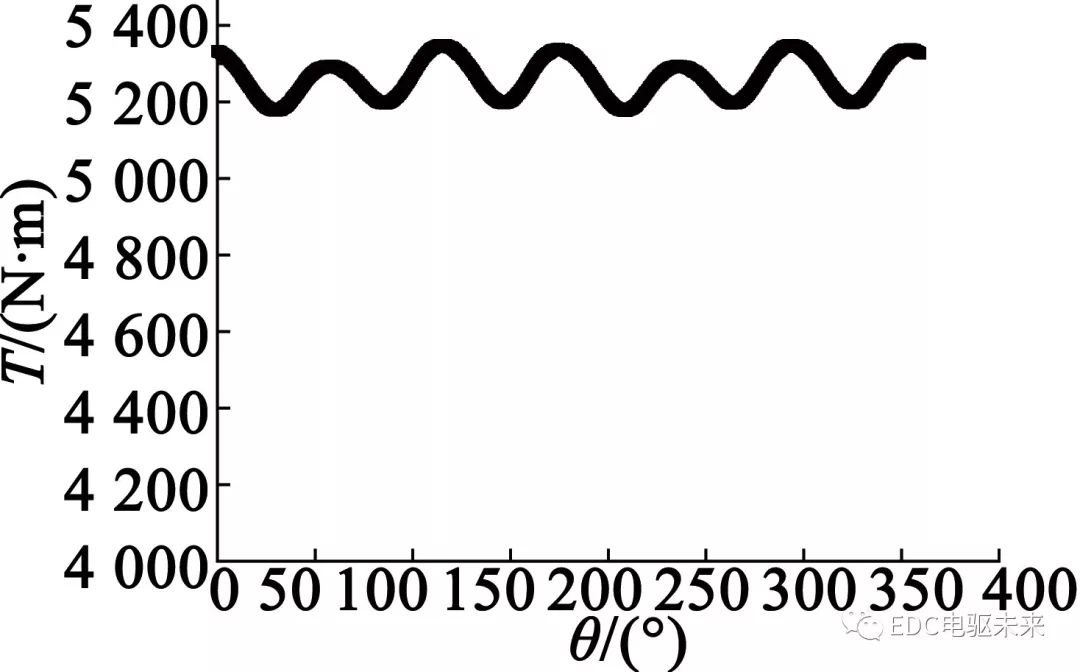
图9 最大输出转矩波形
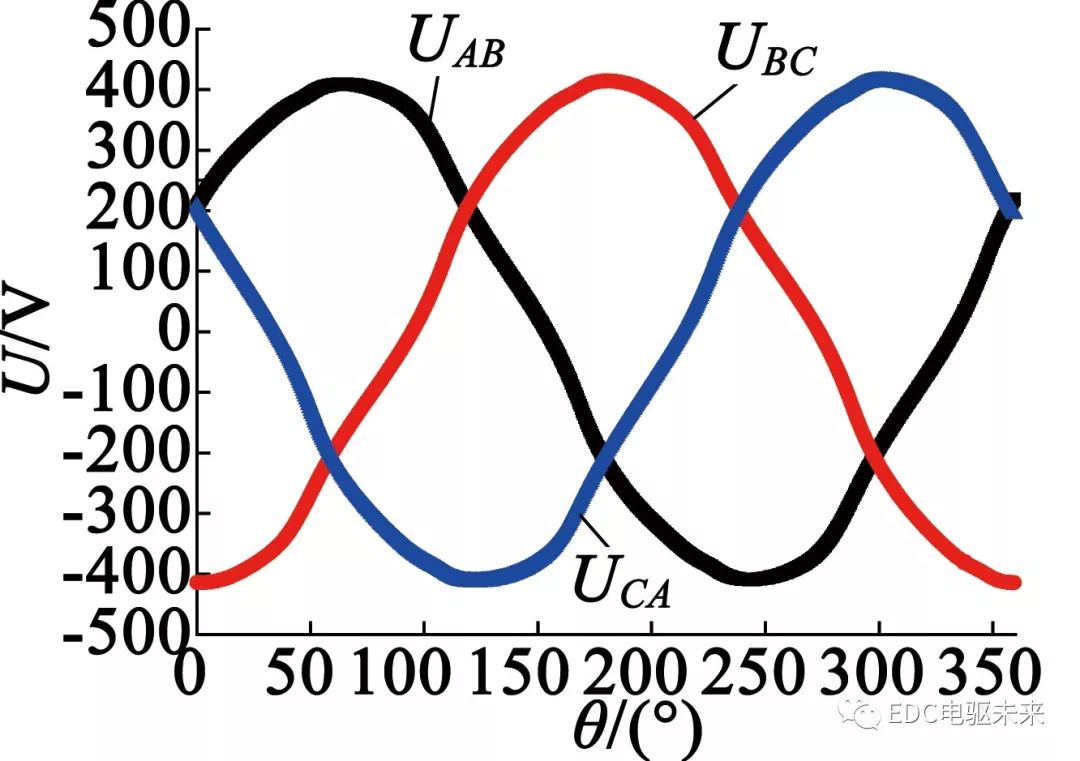
图10 三相感应电势波形
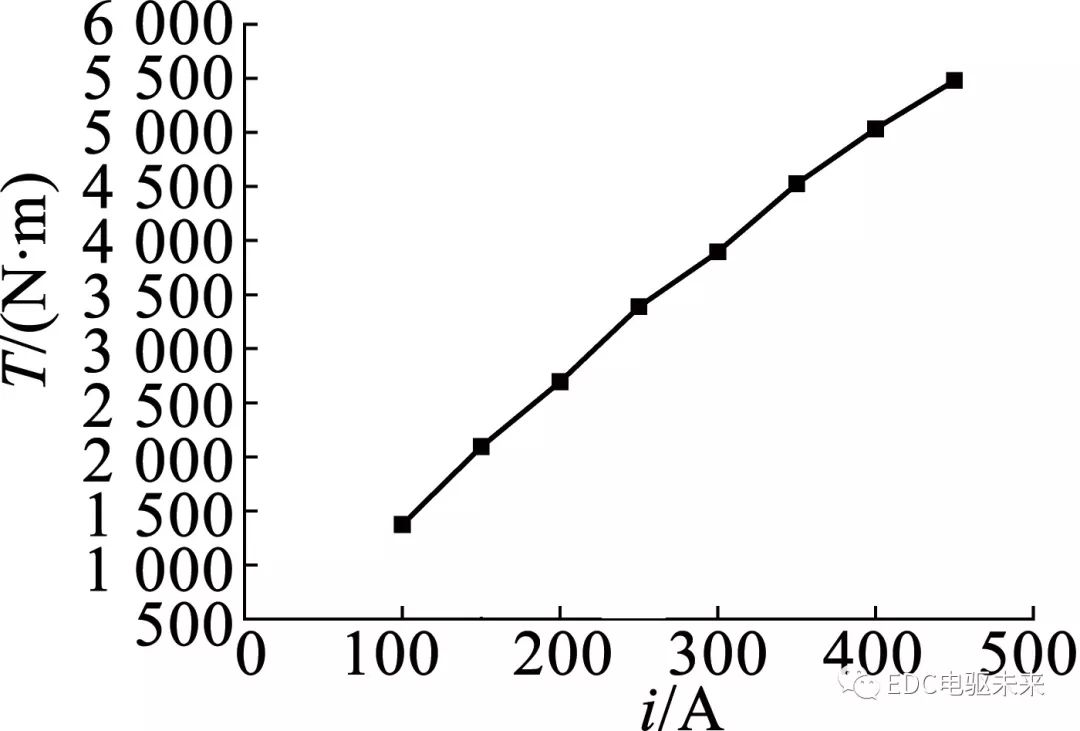
图11 电磁转矩平均值随电流变化曲线
3 永磁轮毂电机性能的优化
机场摆渡车属于地面服务特种车辆,每次承载乘客较多,为了使乘客有舒适的乘车体验并感受到优质的服务水平,对车辆运行的稳定性要求较高。由于齿槽转矩是造成电机波动的主要因素,因此提高摆渡车性能,需要对齿槽转矩进行抑制。空载反电动势同样影响永磁同步电动机的性能。通常永磁电动机的反电动势含有高次谐波,导致波形偏离正弦波,降低控制精度,增加损耗和转矩脉动,造成电机效率下降。因此,削弱电机反电动势中的谐波对提高电机的性能具有重要的意义。
3.1 斜极对齿槽转矩的影响
在引入斜极之后,电机静态特性发生变化,电机轴向的不同截面的磁场分布是不同的,数值计算模型原则上采用三维模型。但三维电磁场分析时间较长,占用计算资源较大,因此仍倾向使用二维数值模型,通过分段计算法进行分析。
其思路是沿电机轴向平均分成若干段,并把每段假设为一个电机,取其二维截面,从而将每段都作为二维模型处理,每一段的电磁场垂直于电机轴向,矢量磁位只有轴向分量。永磁体的斜极模型如图12所示。

图12 永磁体斜极模型
图13为不同永磁体倾斜角度下的齿槽转矩波形,图14为齿槽转矩波动幅值随永磁体倾斜角度的变化曲线。从图14中可以看出,当倾斜角度α为4°时,齿槽转矩波动幅值较小;当倾斜角度α为3°时,齿槽转矩波动幅值较大,达到0.902 N·m。最大波动幅值与最小波动幅值相差0.453 N·m。可见,永磁体斜极对齿槽转矩的影响较小。
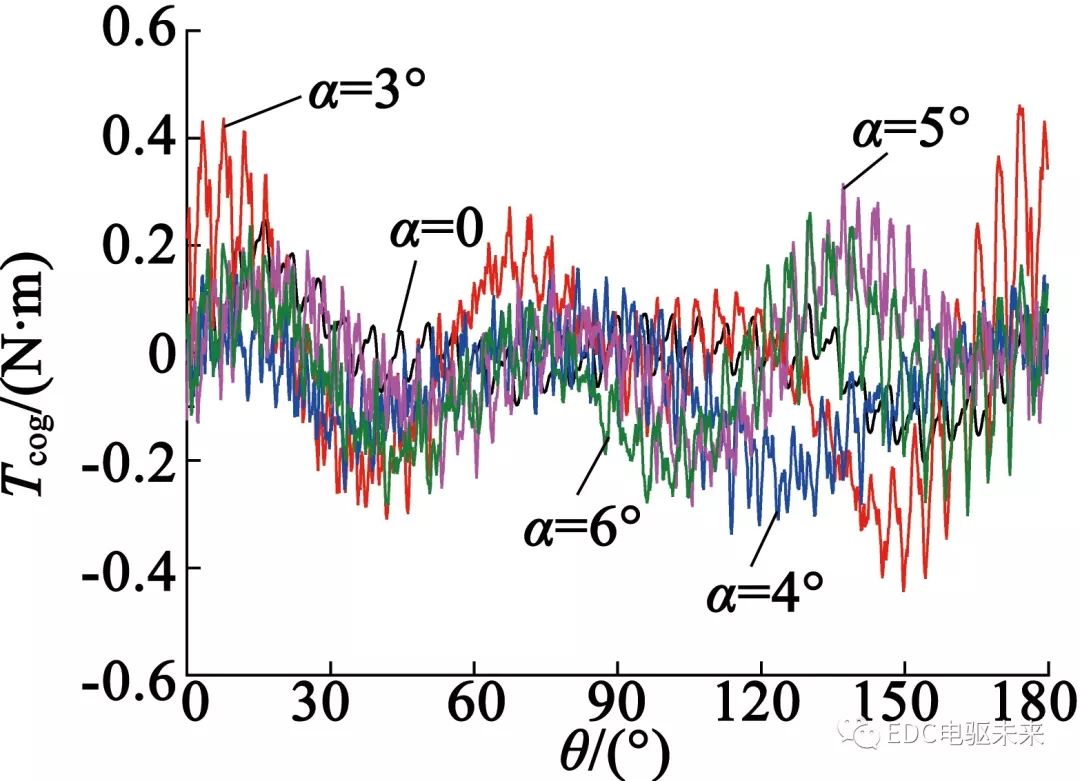
图13 不同永磁体倾斜角度下齿槽转矩波形
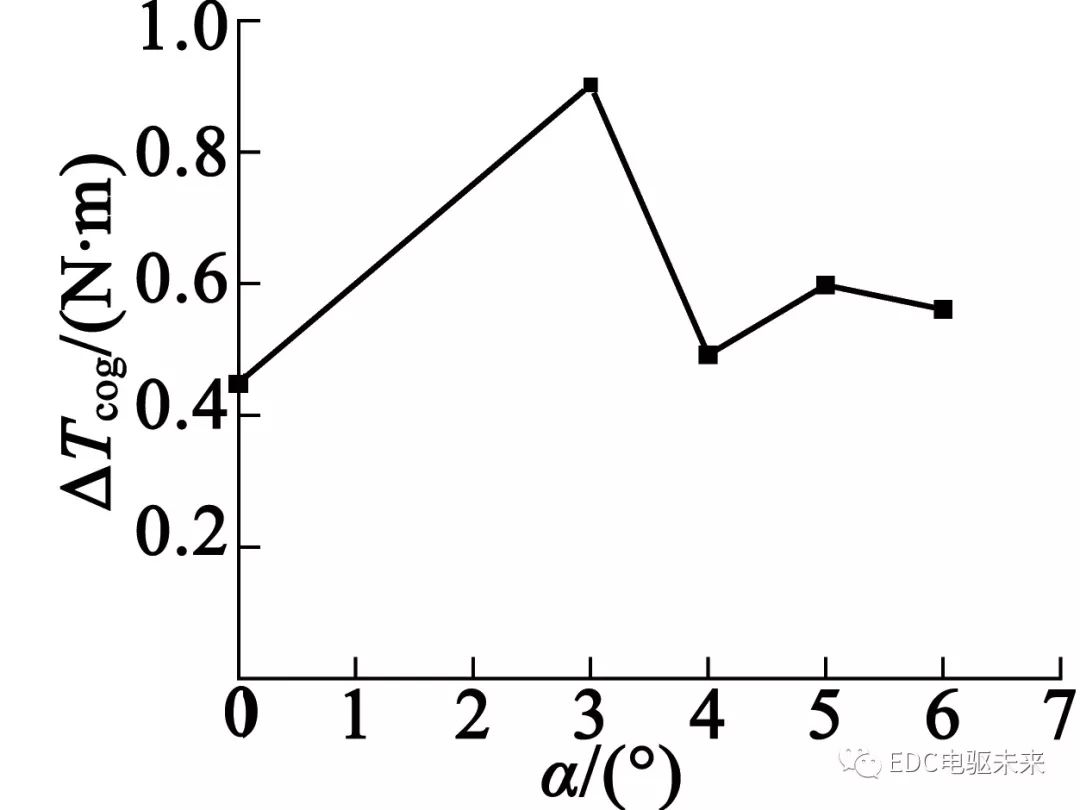
图14 波动幅值随永磁体倾斜角度的变化曲线
3.2 斜极对反电动势的影响
为了更清晰地分析斜极对电机反电动势的影响,本文定义空载反电动势非正弦度系数αE,其在数值上等于反电动势各谐波幅值的绝对值之和与基波幅值之比。
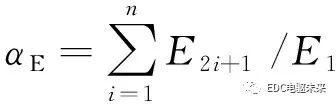
(1)
电机转矩波动中主要是6次谐波,为了减小波动转矩对电机性能的影响,这里首先定义波动转矩系数αT6:
αT6=
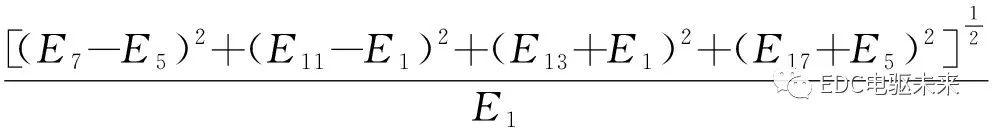
(2)
需要说明的是,上述公式推导忽略了电枢反应对波动转矩的影响,即不考虑定子磁链所产生的波动转矩以及忽略磁场饱和对波动转矩的影响。转矩波动主要是由反电动势和电流的各次谐波相互作用产生的,而本文接下来只对由反电动势5次和7次谐波所引起的转矩波动展开研究,关于由电流谐波造成的转矩波动和高于6次谐波引起的转矩波动不予考虑。
因此,反电动势非正弦度系数式(1)和波动转矩系数式(2)可以简化:
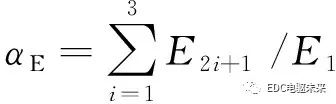
(3)

(4)
反电动势随倾斜角度变化结果如图15所示。可以看出,不同倾斜角度时,反电动势的幅值和相位都发生了明显变化。
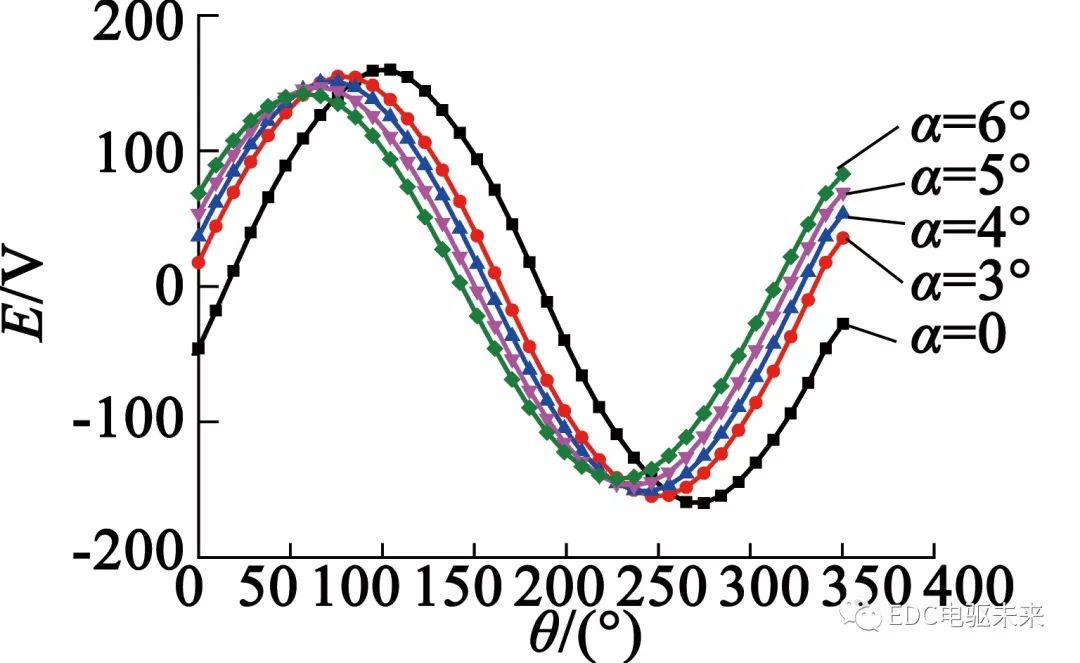
图15 不同永磁体倾斜角度下反电动势波形
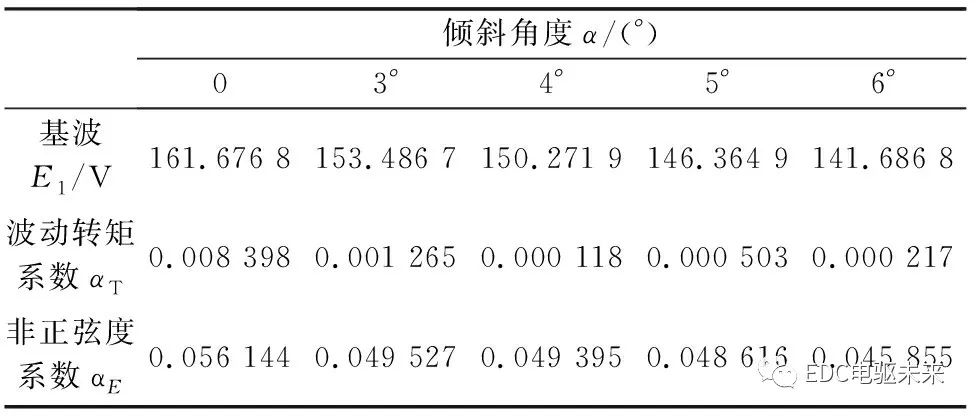
通过对反电动势傅里叶分解,得到反电动势各次谐波随永磁体倾斜角度的变化情况,如图16所示。表2分别给出了在不同永磁体倾斜角度下反电动势基波幅值、波动转矩系数和非正弦度系数的对比结果。可知反电动势基波随永磁体倾斜角度的增加逐渐减小;当倾斜角度为4°时波动转矩系数最小,与最大值相差较大;随着倾斜角度的增加,非正弦度系数呈逐渐下降的趋势。
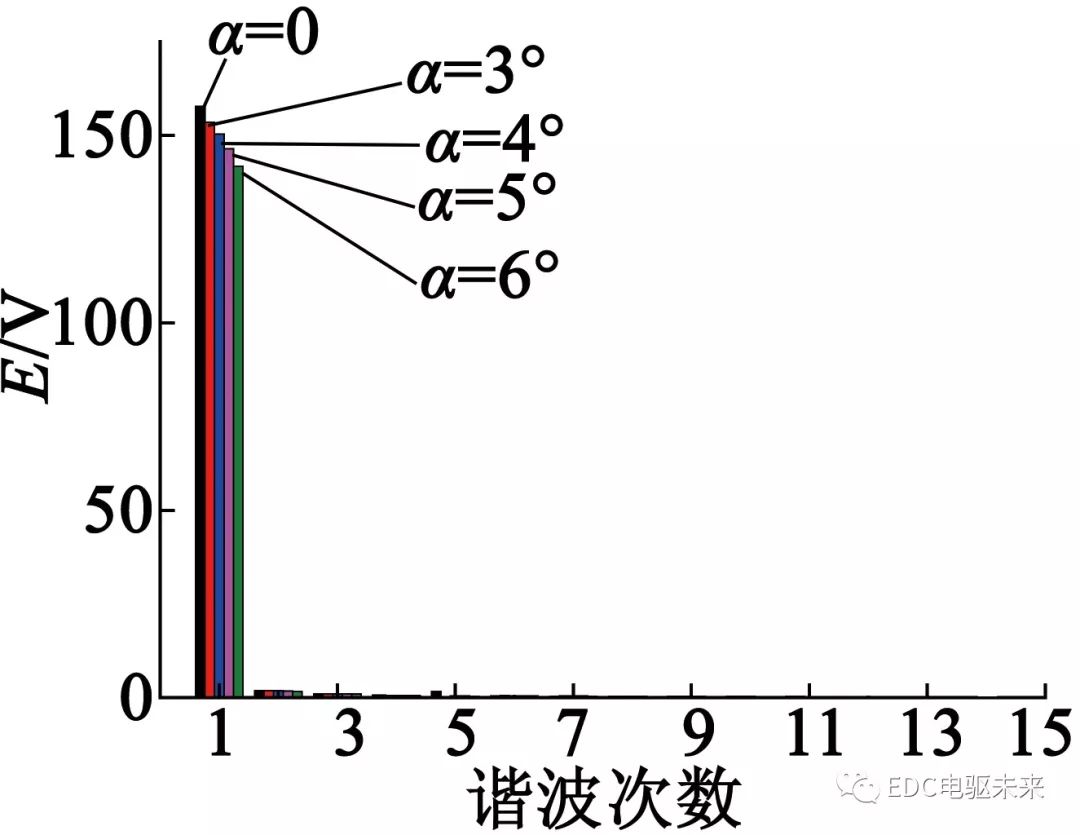
图16 反电动势各次谐波随永磁体倾斜角度的变化情况
表2 不同永磁体倾斜角度下的性能比较
3.3 斜极对电磁转矩的影响
当电机通入300 A电流时,得到不同永磁体倾斜角度下电磁转矩在一个电周期内的波形图,如图17所示。从图17中可以看出,随永磁体倾斜角度的增大,电磁转矩幅值明显下降。图18为电磁转矩波动幅值随倾斜角度的变化曲线。可以看出,斜极对电磁转矩的波动具有明显的抑制效果,但当倾斜角度大于5°时,斜极对转矩波动的抑制效果明显减弱;同时,随着倾斜角度的增大,电磁转矩幅值下降较快。因此,对电机进行斜极设置时,倾斜角度不能太大。为此,本文最终选取永磁体倾斜角度为4°,既保证电磁转矩足够大,又保证转矩波动幅值较小。
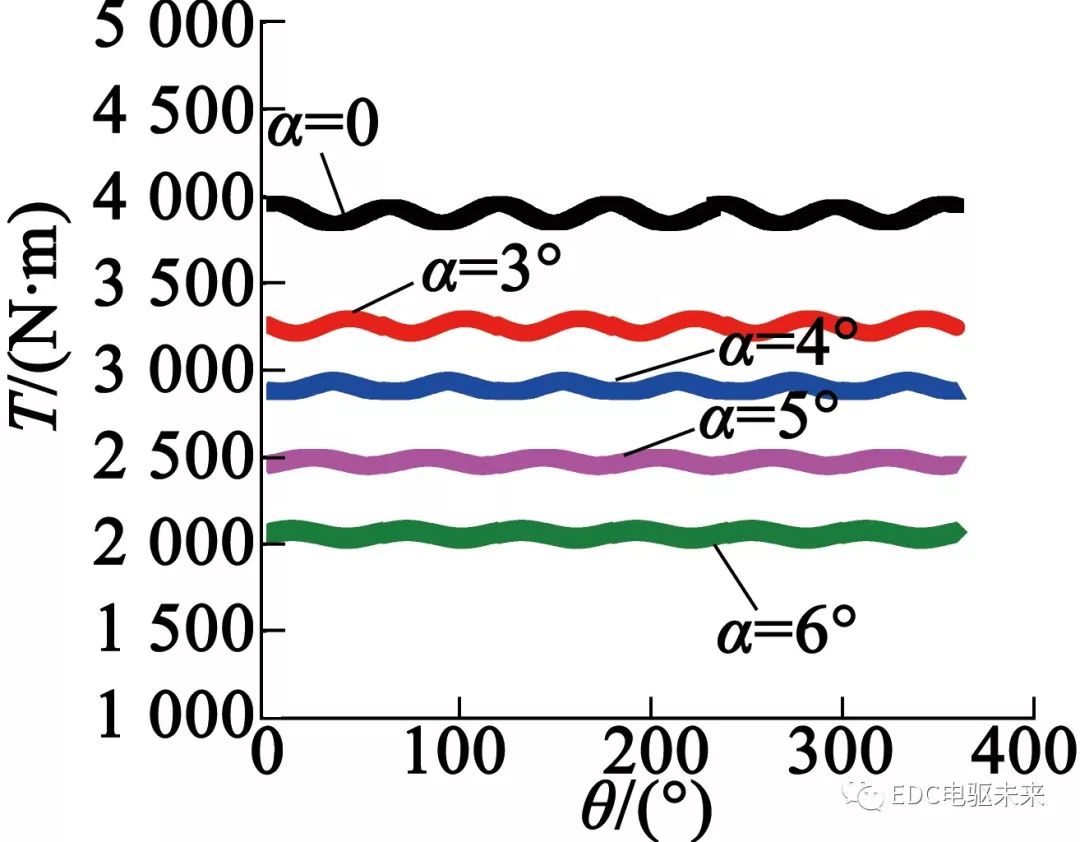
图17 不同永磁体倾斜角度下电磁转矩波形
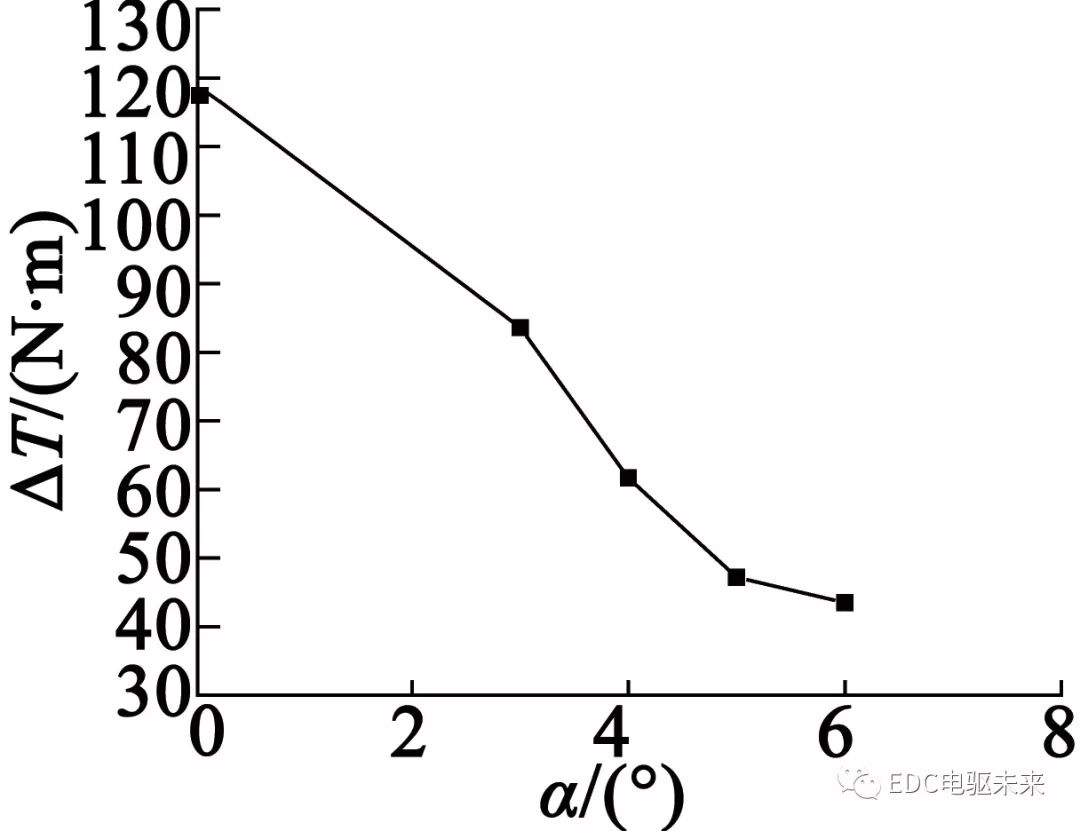
图18 电磁转矩波动幅值随倾斜角度的变化曲线
4 结 语
本文根据机场摆渡车的应用特点,设计出30极99槽永磁同步轮毂电机,主要完成了以下4方面工作。
(1) 为了使永磁同步轮毂电机满足机场摆渡车的性能要求,通过有限元软件对设计的电机进行了空载特性与负载特性分析。
(2) 通过有限元软件计算了转子斜极对齿槽转矩的影响,得出当永磁体倾斜角度为4°时齿槽转矩幅值最小。
(3) 通过有限元软件计算了转子斜极对反电动势的影响,得出反电动势基波幅值随着倾斜角度的增加而下降。波动转矩系数随着永磁体倾斜角度的增加逐渐减小,当倾斜角度为6°时,非正弦度系数最小。
(4) 通过有限元软件计算了转子斜极对电磁转矩的影响,最终本文选取永磁体斜极4°作为所设计的永磁轮毂电机转子斜极的最佳角度。
审核编辑:汤梓红
-
轮毂电机的原理与结构 轮毂电机的优缺点2023-07-24 4581
-
表贴式永磁电机空载时的磁场解析模型建立方案2023-10-30 3461
-
轮毂电机电磁噪声测试方法及特性分析2025-06-10 586
-
汽车轮毂电机的原理和优点2018-10-12 5982
-
【设计技巧】轮毂电机驱动技术2019-07-27 4614
-
什么是轮毂电机技术?轮毂电机有哪些优点及缺点?2021-06-17 2056
-
如何对永磁直流无刷电机进行仿真分析?2021-07-21 2359
-
探讨轮毂电机产业化的发展思路2023-03-01 1182
-
基于ANSYS的电梯驱动用永磁同步电机磁场有限元分析2016-05-04 791
-
轮毂电机的优缺点2017-11-03 28250
-
轮毂电机温度场计算2018-03-28 1087
-
轮毂电机机械结构设计及散热分析2022-12-16 8157
-
轮毂电机与中置电机:哪个更省电?2024-02-24 3022
-
轮毂电机是什么?它有什么注意事项?2024-10-24 2937
-
轮毂电机技术原理及结构2025-09-11 833
全部0条评论

快来发表一下你的评论吧 !

