基于OASIS的移动机器人上传感器布置优化方案

作者：鱼骨  

1. 笔者感悟

本文介绍了一种名为OASIS（Optimal Arrangements for Sensing in SLAM）的新方法，该方法旨在优化移动机器人在SLAM任务中的传感器布置。本文指出了当前存在的研究问题，即目前缺乏关于如何在移动机器人上安装传感器的理论框架。OASIS方法是一种优化设计任何建图或导航系统的方法，该系统将来自多个传感器的独立测量数据进行融合。这里也推荐「3D视觉工坊」新课程深度剖析面向机器人领域的3D激光SLAM技术原理、代码与实战》。

OASIS方法的三个关键组成部分是：

设计空间：由一组有限的候选传感器安装位置组成，用于优化传感器布置。

基于E-最优性的可计算的客观函数：使用地标为基础的SLAM中舒尔补的Fisher信息矩阵的最小特征值作为评估定位精度的信息理论度量。

高效的优化方法：将贪婪传感器选择与基于凸松弛的计算相结合，以验证最优性的上界，从而从候选传感器安装位置集合中提取高质量的解决方案。

本文进一步介绍了如何模拟和优化传感器布置。作者提到，如果机器人预计在多个环境中采取各种轨迹，可以模拟大量异构的场景，以找到在平均情况下表现良好的传感器布置。此外，如果机器人受限于在固定环境中特定路径上操作（例如仓库作业），也可以使用OASIS方法找到适合其特定需求的布置方式。

OASIS方法的优点是：

能够直接获取到机器人底盘机械约束导致的传感器位置有限的情况；

避免了在离散（传感器选择）和连续（传感器位置）变量上进行联合优化的需求；

采用了快速近似的组合优化算法，可以从候选传感器位置集合中高效地获取高质量解决方案。

本文还介绍了如何建模给定传感器布置的SLAM性能，并提出了度量定位精度的信息论度量方法。作者给出了相应的公式，并解释了度量方法的原理。

最后，本文还通过实验评估了该方法的有效性。实验结果表明，该方法在实践中非常有效，可以快速得到比最优模型高1-2%的传感器布置方案。

总之，本文使用了一种名为OASIS的方法来优化移动机器人上传感器的布置。该方法采用了特定的三个关键组成部分，并通过建模和优化来提高SLAM任务的效率和精度。本文提出的方法在实验中表现出色，并具有实际应用的潜力。

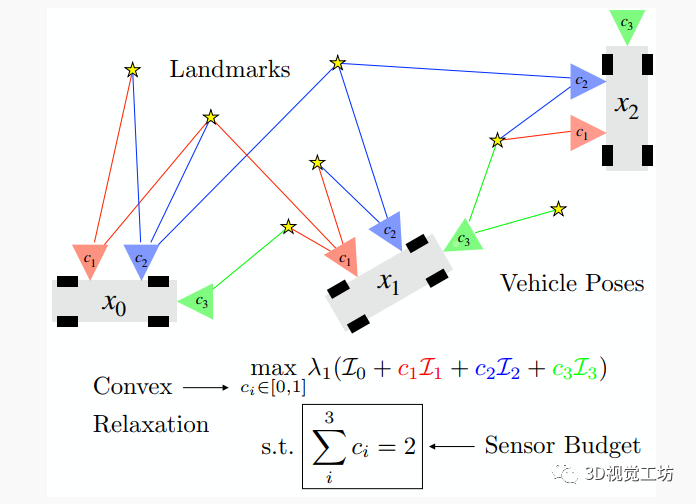
图1：OASIS的流程图。对于每个姿势，传感器能够观测到一部分地标。OASIS的目标是最大化联合Fisher信息矩阵的最小特征值，该矩阵由各个传感器的子矩阵构成。在这个例子中，传感器“预算”要求我们只能从三个可选传感器中选出两个。最后，需要注意的是，表示传感器选择的离散二进制变量被松弛为凸集合。

2. 论文摘要

移动机器人外部传感器的数量和位置对其感知能力有重要影响。设计新的机器人平台时，研究人员和从业者往往会参考现有的配置或使用简单的启发式方法(如视野覆盖率)来确定传感器的位置。然而，这一关键的移动机器人感知问题目前还缺乏明确的理论指导。本文以同时定位与建图(SLAM)为背景，从信息理论角度探讨了移动机器人传感器布局问题。我们把传感器布局问题建模为一个基于E优化准则的最优子集选择问题。由于一般的子集选择问题是NP困难的，我们提出了一种结合贪婪算法和快速凸松弛技术的有效方法，可以在实践中找到可证明最优的传感器设计。

3. 最优传感器布置模型

本节介绍了如何将最优传感器布置问题形式化为一个含有二进制变量的整数规划(IP)问题。

A. 传感器布置空间的参数化

给定机器人底盘的模型，传统方法是先确定要使用哪些类型和数量的传感器，再确定它们在机器人上的安装位置。但是，这种方法会导致一个非常困难的非凸问题，需要同时优化(离散的)传感器选择变量和(连续的)传感器姿势变量。

我们提出了一种不同的方法，将传感器布置问题看作是一个子集选择问题。具体而言，我们假设我们给出的S集合有限地枚举了所有可能的传感器安装位置(即，在机器人底盘上安装特定传感器的特定姿势的决定)。那么，设计一个传感器布置就等于从S中选择一个特定传感器安装位置的子集。

B. 给定传感器布置的SLAM性能模型

本小节介绍了如何根据传感器布置来评估SLAM的性能。

设想我们的移动机器人在一个最初未知的环境中导航，环境中包含个可唯一识别的特征。在机器人探索时，它在一系列姿势中移动，同时从其机载传感器收集测量。设为中的所有候选传感器安装位置生成的完整测量集合。我们假设每个测量都是从已知的传感器模型独立采样的，形式为：

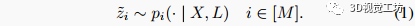
现在考虑我们机器人在候选传感器布置下的SLAM性能。不失一般性，设，我们可以给中的候选项标号1，...，，然后用的二进制向量标识每个的子集，其中定义为：

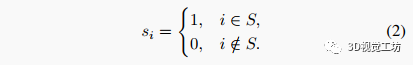
类似地，设为将每个分配给生成第个测量的传感器安装位置的标签的函数。使用这些符号，我们可以将传感器布置下机器人可用的数据联合似然参数化为：

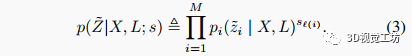
相应的，我们机器人在传感器布置下要求解的SLAM最大似然估计的具体为：

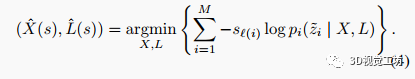
C. Fisher信息和Cramer-Rao下界

Cramer-Rao下界(CRLB)为任何无偏最大似然估计器的可实现协方差提供了一个(在Loewner顺序意义下的)下确界：

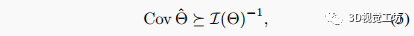
其中右侧的矩阵是Fisher信息矩阵(FIM)：

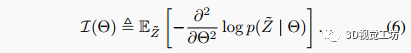
对于SLAM似然度(3)，CRLB的形式为：

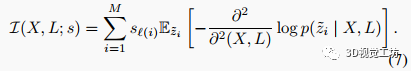
注意测量在(1)中的条件独立性意味着是布置中包含的每个单个观测贡献的信息矩阵之和。等价地，写作：

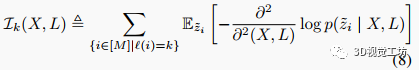
对于由传感器生成的所有测量的信息矩阵之和，则等式(7)等价于：

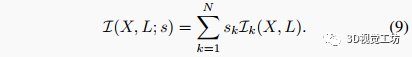
也就是说：传感器布置下SLAM估计问题(4)的FIM仅仅是中包含的每个单个传感器提供的信息之和。

D. 传感器布置的性能准则

CRLB意味着如果我们想从(4)中恢复一个“小”的不确定性的SLAM估计，我们必须选择一个传感器布置，使对应的FIM 尽可能“大”。

为此，我们提出使用E优化准则作为优化传感器布置设计的性能度量。简而言之，这种方法要求最大化的最小特征值。与更常见的D优化(最大化的行列式对数)相比，E优化的优势在于后者取决于的全部谱，而前者仅需要单个最小特征值；即使对非常大的矩阵，这个量也可以非常高效地计算。此外，由于下确界了的谱，最大化这个量可以解释为最大化对数行列式本身的下确界。

我们还注意到，在许多SLAM应用中，我们主要关注机器人姿态估计；特征位置估计只在支持准确的机器人定位的程度上才有趣。在这种情况下，我们主要关注的是最小化，即姿态估计的边缘协方差。鉴于(5)和2×2块矩阵逆公式，与此相关的CRLB形式是：

这里的Schur(I)表示相对于特征变量的广义舒尔补。因此，我们使用以下目标函数：

E. 最优传感器布置

我们现在准备好形式化最优传感器布置问题了。给定候选传感器安装位置的集合，环境和机器人轨迹的一个实例，以及要选择的传感器数量，我们的任务是找到中的基数子集，以最大化目标函数(11)：

问题1(最优传感器布置)。

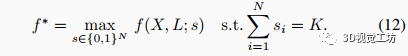
4. 快速近似算法

问题1的全局最优解往往是NP难解的，所以通常无法在多项式时间内得到。我们的算法结合了IV-A节描述的简单贪婪策略和IV-B节提出的凸松弛技术。在这一节中，为了简化符号，我们不再显式地写出和(因为它们不是优化变量)。

A. 贪婪最大化

顾名思义，贪婪集合最大化算法通过迭代构建解集，在每次迭代中，都添加使目标函数的边际收益最大化的元素。当目标函数是规范化单调子模函数时，贪婪解 保证满足

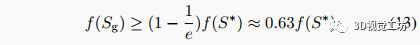
其中是(12)的全局最大值。不幸的是，虽然单调且规范化，但只满足近似子模性。

B. 凸松弛

我们将Problem 1中的(非凸)二进制约束松弛为(凸)布尔约束：

问题2(问题1的布尔松弛)。

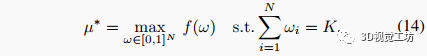
观察到如果是凹函数，那么(14)是一个凸优化问题。因此，问题2的计算可行性取决于我们的目标函数的凹性。幸运的是，下面的命题(在附录中证明)说明E优化性能准则确实是凹的。

命题1(的凹性)。在域上定义的函数是凹的。

于是问题2在使用E优化准则(11)时是一个凸优化问题，因此可以使用标准的凸优化方法全局最优解决。我们因此建议使用Frank-Wolfe方法求解问题2。

让我们考虑问题1和2的最优值比较。由于问题2是问题1的松弛，其最优值为问题1的最优值提供了一个上确界。另一方面，对于问题1中的任何可行的，我们显然有。这些不等式一起意味着：

对问题1中的任何可行的，有

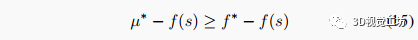
(15)式的重要性在于，它使我们能够使用问题2的最优值来给定问题1中任何可行解的次优性。特别是，正如我们将在第V节中看到的，这将提供一种实用的方法来验证问题1的候选解的(全局)最优性。

C. OASIS算法

算法1

算法1概述了OASIS的整个过程。简单来说，我们的方法是先用顺序贪婪集合最大化算法得到问题1的一个可行解，再用Frank-Wolfe算法求解凸松弛问题2，得到问题2的最优值上界，然后利用(15)式给出的次优性界限。这种简单的方法能够在实际中有效地找到传感器布置问题(12)的可验证最优解。这里也推荐「3D视觉工坊」新课程深度剖析面向机器人领域的3D激光SLAM技术原理、代码与实战》。

5. 评估

本文通过贪婪算法和凸优化方法进行了实验评估，并从信息论标准和SLAM性能两个方面进行了结果呈现。在贪婪算法的实验结果中，通过可视化展示了优化结果的图像，从图中可以看出在不同情况下相机位置的偏好。而凸优化方法的实验结果中，作者通过图表等方式展示了优化结果与最优值之间的接近程度。实验结果表明，本文提出的OASIS方法在实践中非常有效，并能够得到接近于最优值的传感器布局。需要注意的是，虽然目前的实验重点是对视觉SLAM任务的相机选择，但作者将在未来的工作中探索更广泛的传感器配置设计，包括异构传感器集和更多的设计约束。

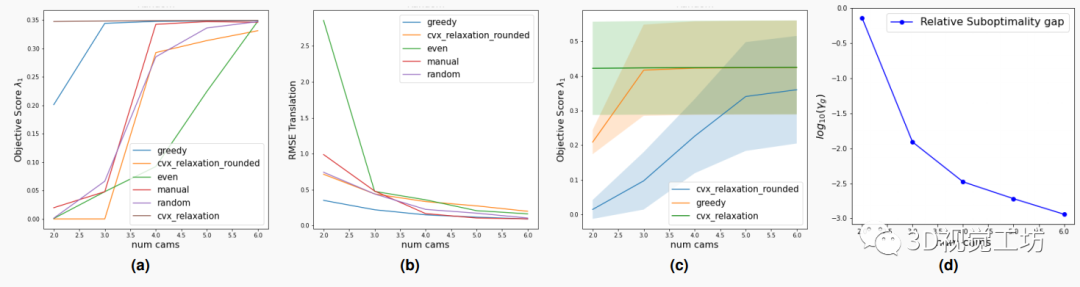
图2：实验结果I：在合成数据集上对最佳相机布置的定量结果。通过对优化目标函数的中位数优化分数和从最优相机选择的图计算出的位姿估计的平均一二乘误差（RMSE）与地面实况的比较，展示了OASIS算法的效果。图(c)展示了贪婪优化和凸松弛解在k-max舍入前后的目标分数。贪婪优化得到了接近最优解的解，如与未舍入的凸松弛方法的分数的接近程度所示，凸松弛方法给出了最优值的上界，特别是对于来说。（d）展示了贪婪优化和凸松弛方法的运行时间比较。贪婪方法的时间复杂度随着相机数量的增加而线性增长，而对凸松弛方法影响不大。

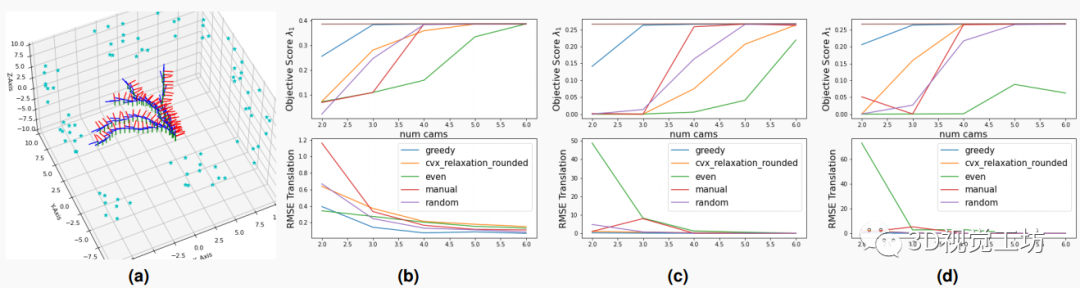
图3：实验结果II：(a)用于合成数据收集的设置。一个模拟的类似房间的环境包含墙壁上的地标和从顶视图显示的随机样本轨迹。(b-d)圆形、前向和横向运动的基准算法的定量结果。

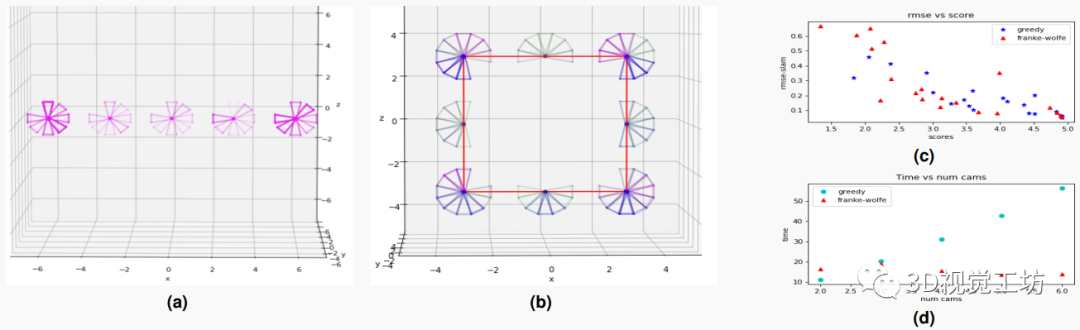
图4：实验结果III。贪婪最优选择在多个实验中的可视化，叠加在候选池（a）上，其在线性阵列配置和（b）无论是在平移方向还是方向上都是定期间隔的地方。更深/更暗的颜色表示选择的频率更高。(c)显示评分与SLAM姿势估计的RMSE之间的相反关系，对于贪婪优化和凸松弛方法都是如此。因此，E-优化改善了SLAM性能。(b)贪婪优化与凸松弛方法的运行时间比较。贪婪方法的时间复杂度与相机数量呈线性增长，而对于凸松弛方法影响不大。

6. 结论

在本文中，我们提出了OASIS方法，用于优化地在一个用于执行SLAM的移动机器人上布置传感器。我们的方法将设计任务形式化为在一个可计算的E-最优性性能度量下的最优子集选择问题。虽然子集选择问题在一般情况下是NP难解的，但我们也开发了一种快速的近似优化方案，它结合了贪婪的传感器选择和基于凸松弛的事后次优性界限。我们的实验评估表明，OASIS方法在实践中非常有效，能够高效地恢复传感器布置，其与最优值相差1-2%。虽然我们目前的实验主要集中在视觉SLAM任务的相机选择上，但在未来的工作中，我们将探索更广泛类别的传感器装置的设计，包括异构传感器集合和比基数更丰富的设计约束。

编辑：黄飞