

电路如何进行逻辑运算
描述
2.1. 数字逻辑
布尔对传统逻辑学进行数字化,创立一门新的学科:逻辑代数(人们习惯成为布尔代数)。在布尔代数里,用字母来表示一个命题,用1代表命题为真,0代表命题为假。如果A命题是真的,则
A = 1
否则
A = 0
在逻辑学中,如果各个支命题是并列关系,称为“联言命题”,通常用“而且”来连接。为了表示这种逻辑关系,布尔代数使用“×”这个符号。这样,一个联言命题可以表示成:
A × B
为了方便也写成 A • B 或者简化成 AB。
如果支命题都为假,推理结果是假,表示为: A × B = 0 × 0 = 0
如果支命题不全为假,推理结果是假,表示为:A × B = 0 × 1 = 1 × 0 = 0
如果支命题都真,推理结果为真,表示为:A × B = 1 × 1 = 1
表 2-1 联言命题的真值表
| A | B | A × B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
在逻辑学中,如果各个支命题用“或者”“要么”来连接一种选择关系,称为“选言命题”。为了表示这种逻辑关系,布尔代数使用“+”这个符号。这样,一个联言命题可以表示成:
A + B
如果支命题都为假,推理结果是假,表示为: A + B = 0 + 0 = 0
如果支命题不全为假,推理结果是真,表示为:A + B = 0 + 1 = 1 + 0 = 1
如果支命题都真,推理结果为真,表示为A + B = 1 + 1 = 1
表 2-2 选言命题的真值表
| A | B | A + B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
除此之外的第三种逻辑关系是“非”,任何命题,比如命题A,不管是真是假,它的对立面是“非A”,可以表示成 。显然, 如果,则;如果,则。
2.2. 逻辑电路
香农在1936年在其论文《继电器和开关电路的符号化分析》中系统化的阐述了逻辑系统和电路通断之间的关系。如果用X代表一个普通开关组成的电路,那么,X=1就表示开关合上;X=0表示开关打开,如图 2-1(a)。
联言命题演算相当于两个开关X和Y的串联,如图 2-1(b)所示,只有当两个开关都接通的时候,整个电路才是通的;两个都断开,或者其中任何一个断开,整个电路是断开的。选言命题演算相当于两个开关的并联,如图 2-1(c)所示,两个开关只要任何一个接通,或者两个同时接通,整个电路就被接通;只有两个开关同时断开,整个电路才是断开的。
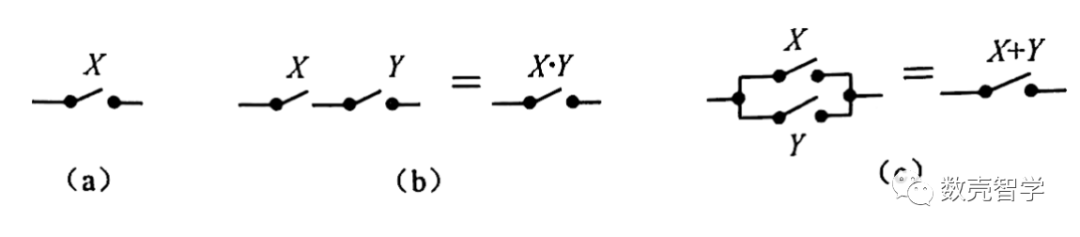
图 2-1 命题演算和现实的开关组合具有一致性
按照这种观点,布尔代数公式也有了新的解释,见表 2-3。
| 布尔代数 | 对应的开关电路 |
|---|---|
| 0 · 0 = 0 | 一个断开的开关和另一个断开的开关串联,整个电路还是断开的 |
| 0 + 0 = 0 | 一个断开的开关和另一个断开的开关并联,整个电路是断开的 |
| 1 · 1 = 1 | 一个闭合的开关和另一个闭合的开关串联,整个电路是连通的 |
| 1 + 1 = 1 | 一个闭合的开关和另一个闭合的开关并联,整个电路是连通的 |
| 1 + 0 = 0 + 1 = 1 | 一个闭合的开关和另一个断开的开关无论以什么顺序并联,整个电路都是连通的 |
| 1 ·0 = 0·1 = 0 | 一个闭合的开关和另一个断开的开关无论以什么顺序串联,整个电路都是断开的 |
表 2-3 布尔代数与开关电路的对应关系
2.3. 开关电路
上一节降到通过控制电路中的开关的闭合与断开,可以控制电路的状态(通电为1,不通电为0)来实现逻辑运算。但这里还有一个很大的问题,电路中的开关不能用手操作,如果用手去操作,逻辑电路就无法扩大规模和提高效率,不能实现自动化,不会有现代大规模集成电路的出现。幸好,我们找到一种用一个电路来控制另一个电路开关的方法,设计出”开关电路“。

图 2-2 用开关电路组成一个报警系统
如图 2-2所示的例子中,左边是一个大型的机电设备,需要对其工作状况进行监控,如果设备运行遇到故障,则及时报警。机电设备电路和报警器是两个独立的电路,可能两个电路的运行电压都不相同,开关电路盒子里面的设计需要做到左边机电设备电路能控制右边报警电路。
为了实现这样的功能,我们在开关电路中引入“继电器”。如图 2-3是一个简单的继电器的例子,图中开关、电源和被电线围绕的电磁铁组成电路A,当电路通电时,金属柱具有磁吸功能,吸引“街铁臂”向电磁铁靠拢。可以想象,如果“街铁臂”是另一个电路B中的开关触头的话,只要位置设计合理,可以达到电路B中的开关被闭合的效果。图中电路A就是一个继电器的原理图。

图 2-3继电器的例子——摩尔斯电报示意图
在明白了继电器的原理之后,我们把图 2-2中的开关电路部分的电路示意图绘制出来(如图 2-4)。通过一个继电器装置,使得机电设备的电路A能够非接触的控制报警电路B。

图 2-4开关电路的内部逻辑——继电器的应用
继电器的引入实现开关电路的意义非常重大,从这以后,我们就能实现用一个电路控制另一个电路,“大规模集成电路群”也变得可能,这是现代化电子计算机出现的基础。
2.4. 逻辑电路实现
在介绍完开关电路等知识的基础上,我们终于可以介绍用电路实现“非”、“而且”、“或者”的逻辑运算。
2.4.1. 非门的实现
首先我们进一步把图 2-4的图简化成示意图(图 2-5)。图中当A电路中开关闭合(机电设备正常工作)的时候,继电器J吸引F电路的开关打开,F电路的负载(喇叭)不工作;当A电路开关打开(机电设备异常造成电路无电流),继电器J失去磁性,F电路的开关在弹簧装置的作用下闭合,F电路复杂(喇叭)工作,发出警报。

图 2-5用继电器控制电路的示意图
在这个例子中,F电路是输出,A电路是输入,发现F的状态与A的状态完全相反,这个电路设计实现了逻辑学中的“非”操作,这个电路逻辑用公式描述是:。
我们对电路的表现方式做进一步的简化,使得在后面进一步解释的时候更加简介明了。

图 2-6各个电路共用电源

图 2-7 为了少绘制连线,使用“接地”符号
如果我们把图 2-7中的阴影部分独立出来,就是一个具有逻辑“非”操作的电子元件,成为“非门”。图画成图 2-8:

图 2-8非门的构造
在绘制电路图的时候,非门用更简单的符号表示(图 2-9):

图 2-9 非门的符号
非门实现了逻辑否定,即逻辑非:

2.4.2. 与门的实现
有了上面的基础,我们可以很容易的看懂“与门”的电路结构图(图 2-10),输出电路F有两个开关分别对应A、B两个输入电路的继电器J1、J2,当A电路通电时,J1对应的开关闭合,当B电路通电时,J2对应的开关闭合。因为F电路的两个开关是串联,所以只有当A、B电路同时通电(输入1)的时候,F电路通电(输出1)。发现F和A、B的逻辑关系如表 2-4。表达式是:F = A • B
表 2-4 与门的输入、输出逻辑关系
| A | B | F |
|---|---|---|
| 断开 (0) | 断开 (0) | 断开 (0) |
| 断开 (0) | 通电(1) | 断开 (0) |
| 通电(1) | 断开 (0) | 断开 (0) |
| 通电(1) | 通电(1) | 通电(1) |

图 2-10 与门的简化电路图
与门在电路图中简化的画法是:

图 2-11 与门的符号
2.4.3. 或门的实现
“或门”的电路结构图(图 2-12),F电路是一个并联电路,两个开关处于并联电路的两个支路上,也就是说这两个开关,至少有一个闭合,F电路就是通路。同上节所述,两个开关分别由A、B电路的继电器J1、J2控制,则,F和A、B的逻辑关系如表 2-5。表达式是:F = A + B 。
表 2-5 或门的逻辑输入、输出逻辑关系表
| A | B | F |
|---|---|---|
| 断开 (0) | 断开 (0) | 断开 (0) |
| 断开 (0) | 通电(1) | 通电(1) |
| 通电(1) | 断开 (0) | 通电(1) |
| 通电(1) | 通电(1) | 通电(1) |

图 2-12 或门的简化电路图
或门在电路图中简化的画法是:

图 2-13 或门的符号
2.5. 常用逻辑芯片介绍
2.5.1. 非门芯片XL74LS04

图 2-14六路非门芯片针脚原理图
2.5.2. 与门芯片XL74LS11

图 2-15三路3输入与门芯片针脚原理图
2.5.3. 或门芯片CD7042BM96

图 2-16二路4输入或门芯片针脚原理图
2.6. 小节
本章主要介绍了电路如何进行逻辑运算,从数字逻辑的布尔代数讲到用电路如何实现简单的逻辑运算,并最终阐述了“非”、“与”、“或”、“异或”四个基础逻辑运算,设计了非门、与门、或门、异或门四个基础电路。在此预告这几个门的重要性,后面复杂的集成电路或者芯片的设计,几乎都是由此类简单的门电路来实现。
-
单片机的逻辑运算符和位运算符是什么?数字电路中的常用符号2018-10-03 27898
-
逻辑运算符是什么2021-07-14 1318
-
逻辑电路与逻辑运算符2021-07-16 1379
-
基本逻辑运算2009-04-06 3527
-
逻辑运算,什么是逻辑运算2010-04-13 33009
-
逻辑运算与移位指令2011-07-03 1253
-
单片机的逻辑电路与逻辑运算的介绍2019-01-29 8347
-
51单片机的算术和逻辑运算功能介绍2019-09-14 5221
-
数字电路基本逻辑关系及其逻辑运算资料汇总2021-12-03 1084
-
单片机逻辑电路与逻辑运算2022-02-10 693
-
三种基本逻辑运算介绍2023-03-23 9116
-
KUKA机器人的逻辑运算符2023-07-21 3560
-
verilog的逻辑运算符2023-09-21 3857
-
PLC中的逻辑运算方式有哪些2024-07-24 2176
-
复合的逻辑运算2025-01-16 583
全部0条评论

快来发表一下你的评论吧 !

