加法器电路设计过程

生活中加减乘除是多么简单的事情，小学一年级的小朋友已经能熟练的掌握。本书主要是面向大学本科以上的读者，却直到第三章才敢小心翼翼的提出如何让电路做加法运算，也不得不感叹，人们设计出计算机是花费了多么大的心血。

首先我们要看看电路如何去做加法。

3.1. 一位加法器设计

首先我们来看二进制加法的具体步骤（以0101 + 0011为例）（如图 3-1），数字的最右边为第0位，往左依次是第1、2、3位。步骤如下：

1.把0101 用A表示，0011用B表示，相加的和用S表示；A的第n位用An表示，B的第n位用Bn表示，S的第n位用Sn表示；用Ci表示当前位来自前一位的进位；

2.第0位二进制相加，A0 + B 0 = 1 + 1 = 10 ，则S0 = 0，C1 =1；

3.第1位二进制相加，A1 + B1 + C1 = 0 + 1 + 1 = 10 ，则S1 = 0， C 2 =1 ；

4.第2位二进制相加，A2 + B2 + C2 = 1 + 0 + 1 = 10 ，则S2 = 0， C 3 =1 ；

5.第3位二进制相加，A3 + B3 + C3 = 0 + 0 + 1 = 01 ，则S3 = 1， C 4 =0 ；

6.所以最终的结果是：C4S3S2S1S0 = 01000

图 3-1 二进制相加的例子

从上面的例子中总结出一位加法器的设计需求。两个二进制数字的对应位数字相加的需求，需要3个输入，2个输出（如图 3-2）。A和B是来自加数和被加数的两个比特；Ci是来自前一个比特位的进位；S是前面三项加起来的“和”；C0是当前这一位向下一位的进位。

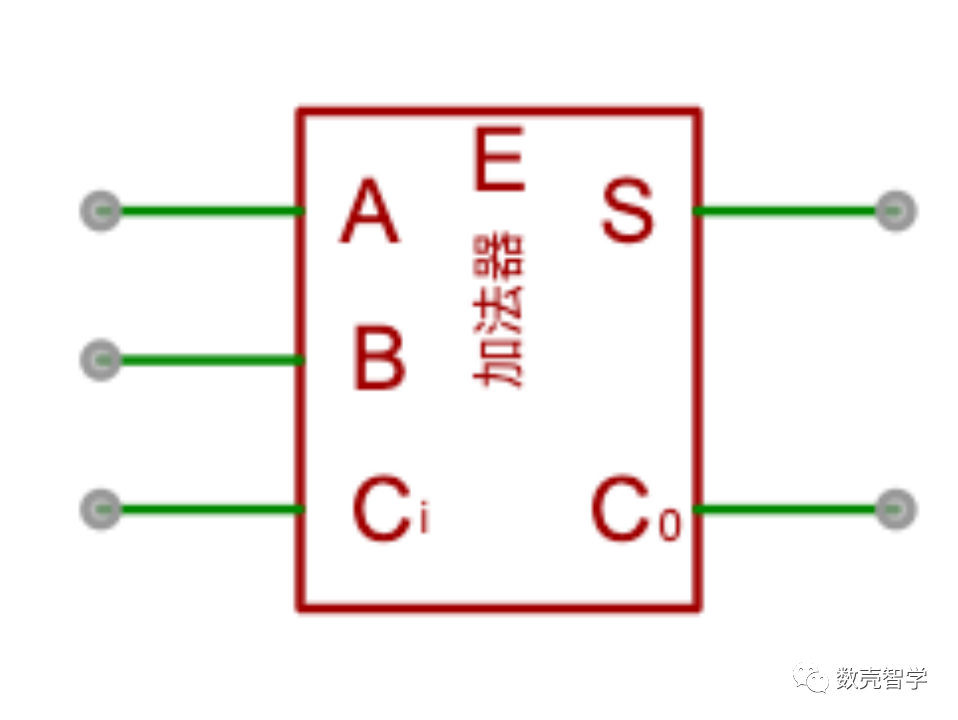
图 3-2 一位加法器的符号

我们可以发现一个3个输入，2个输出的元器件，可以列出所有的输入输出的可能数值，具体如表 3-1 。设计电路的方法就是找到一个电路集合，能够同时满足表中的8种输入输出情况的逻辑，也就是当输入的A、B、Ci为某一行的值的时候，S、C0的输出同时要符合表中列出的数值，比如参照第5行，当输入A=1、B=0、C ~i~ =1，的时候输出S=0、C ~0~ =1。

表 3-1 一位加法器真值表

序号	A	B	Ci	S	C0
1	0	0	0	0	0
2	0	0	1	1	0
3	0	1	0	1	0
4	0	1	1	0	1
5	1	0	0	1	0
6	1	0	1	0	1
7	1	1	0	0	1
8	1	1	1	1	1

我们可以分成两部分来考虑，第一部分是输入A、B、C i， 输出S的电路设计；第二部分是输入A、B、C i， 输出C0的电路设计；这是两个独立的电路，为了实现完整的一位加法器功能的模块，把两个电路以放在一起就行了。

对于第一部分电路，从表 3-1中可以看出，第2、3、5、8行等于1，其他行等于0。S的逻辑表达式只需要满足2、3、5、8行的其中一种输入情况（“或”的逻辑关系），另S =1。则S的完整逻辑表达式为：

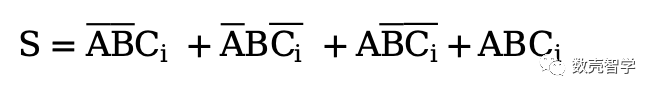
同理，第二部分电路设计中，C0的完整逻辑表达式为：

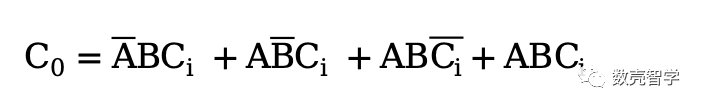
如果对逻辑表达式的设计还不是非常熟悉的读者，可以用这两个逻辑表达式来验证表 3-1，对于每一行的A、B、Ci的输入，输出的S和C0的值都完美的对应。

接下来的电路设计，把逻辑表达式中的“与”、“或”、“非“的逻辑关系变成电路中的“与门”、“或门”、“非门”，在加上连线就是我们需要的加法器的电路图。直接上图（图 3-3）：

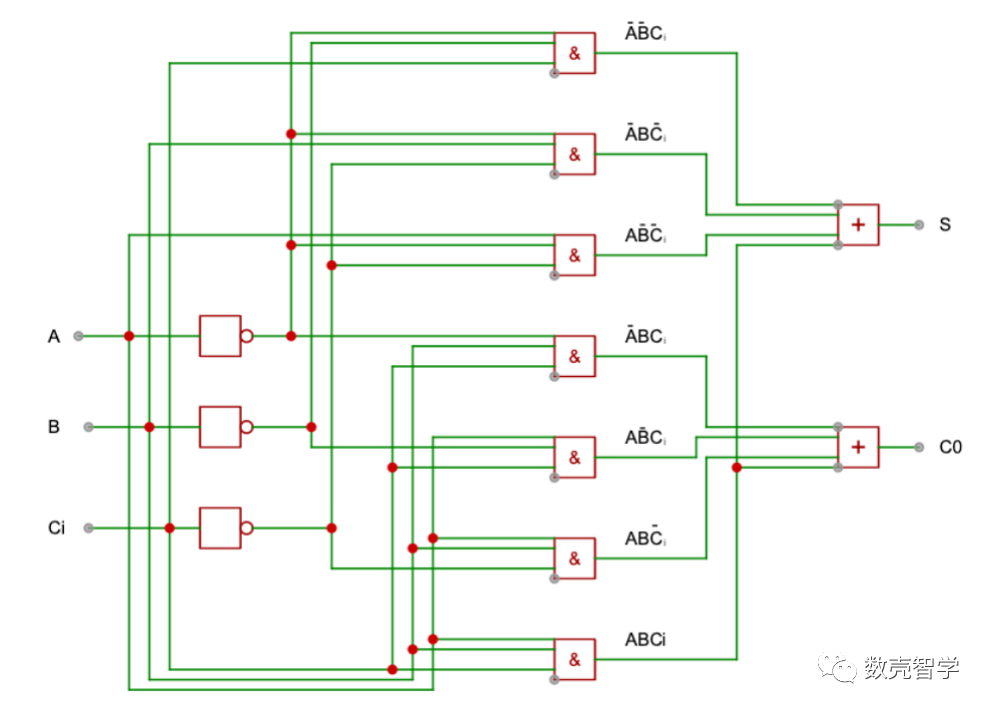
图 3-3 加法器的逻辑电路图

3.2. 加法实验电路

用三个商用的“非门”（图 2-14）、“与门”（图 2-15）、“或门”（图 2-16）芯片组成实际的加法器实现电路图（图 3-4）。

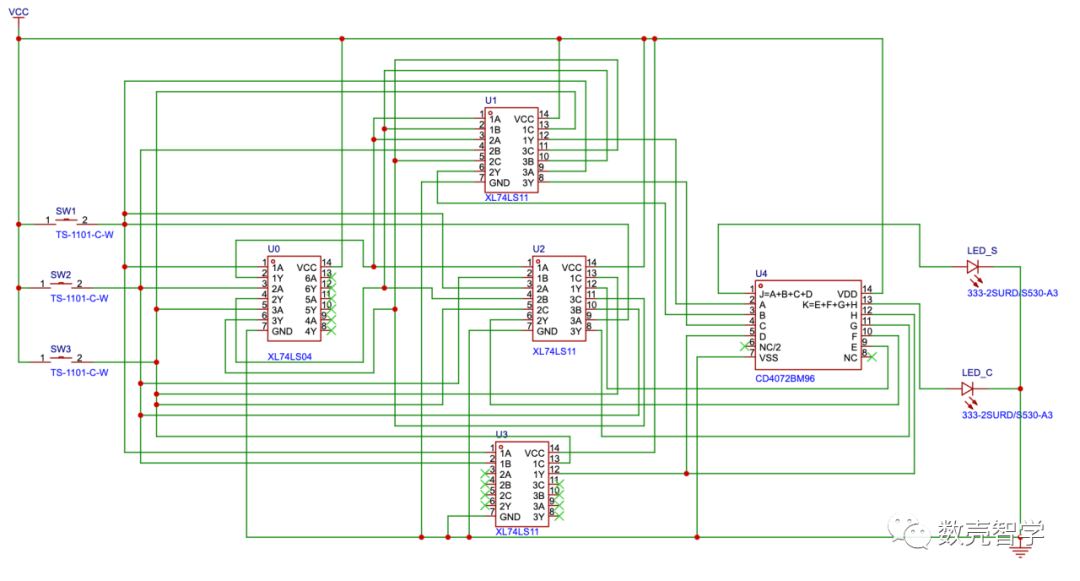
图 3-4根据逻辑门芯片绘制的加法器电路原理图

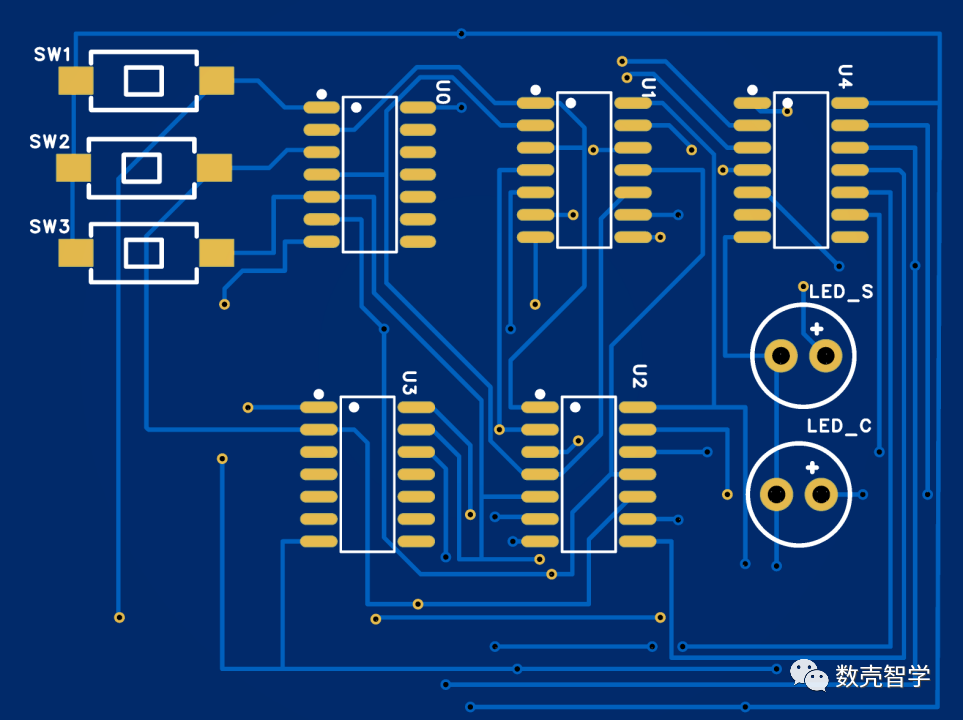
图 3-5根据门电路芯片设计的加法器PCB板（正面）

3.3. 用加法器实现加法

两个二进制数字相加为例，利用加法器设计电路图实现二进制加法。

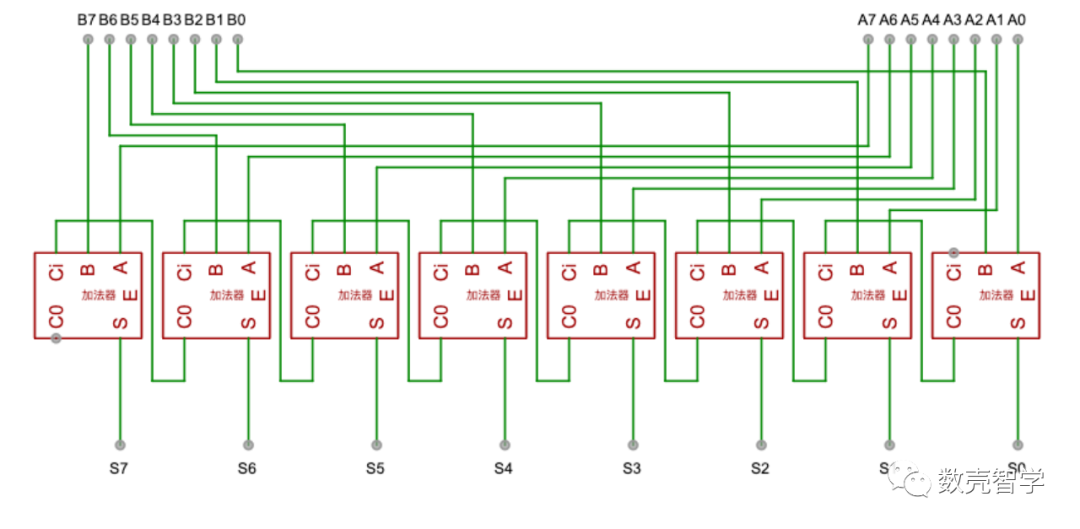
图 3-6用加法器组成一个八位加法电路

将图 3-6简化成8位加法器示意图：

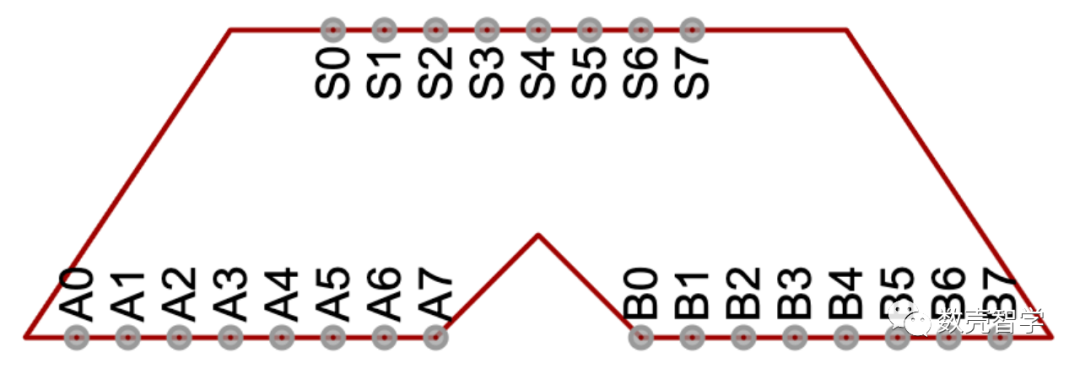
图 3-7 八位加法器的示意图

3.4. 加法实验

3.4.1. 常用全加芯片XD74LS283

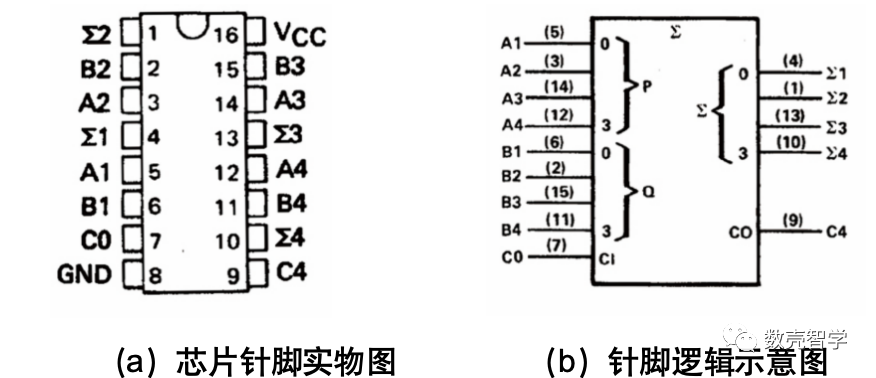
图 3-8 四位加法器XD74LS283针脚示意图

3.4.2. 加法实验

本实验采用常用的4位加法器芯片（XD74LS283）（如图 3-8）实现两个8位二进制相加的实际电路。

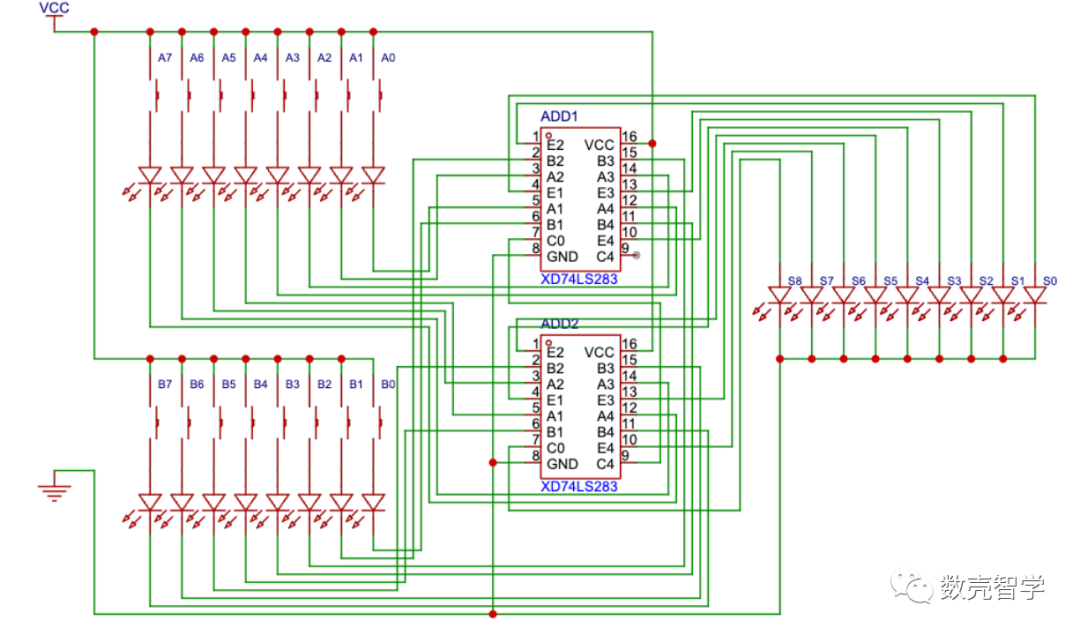
图 3-9八位加法实验电路图

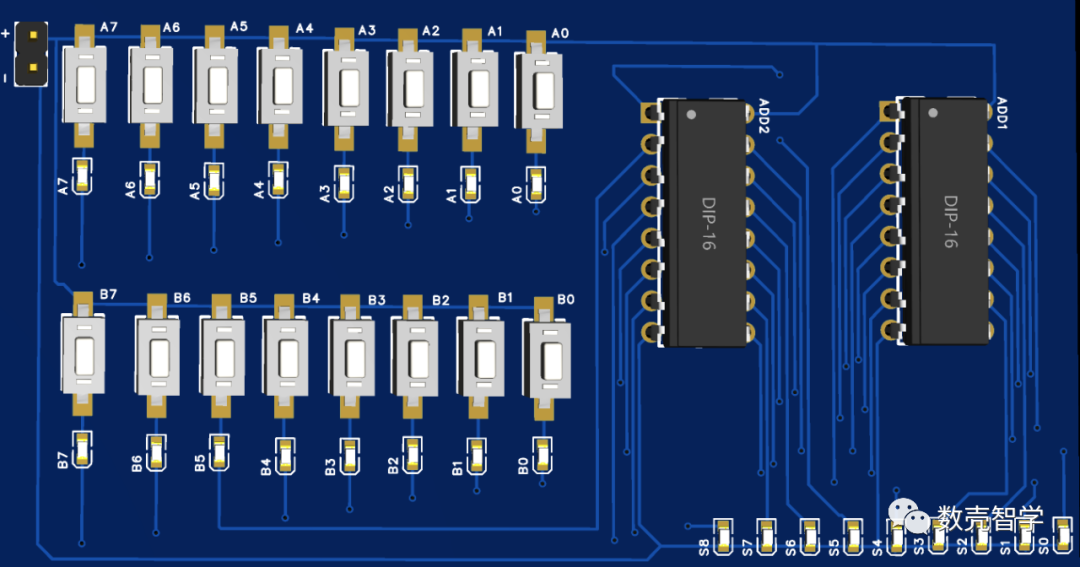
图 3-10 八位加法实验板

3.5. 小节

本节通过完整的阐述了加法器这个电子元件的电路设计过程，从元件功能需求分析到逻辑表达式的建立到逻辑电路图的设计。