

基石数据:TOC理论物理学浅析(一)
描述
01|合力加矢量Fa对mv的影响
在TOC理论的解析中,常常引用广义动量定理FαT=Mv,来源于牛顿第二定律F=mα,F=m△v/t,Ft=m△v,其中F是合力,所以引入矢量α,m是质量,△v是增速,后续在其他章节在说明合力加矢量Fα对mv的影响。
02|瓶颈点是系统的关键点
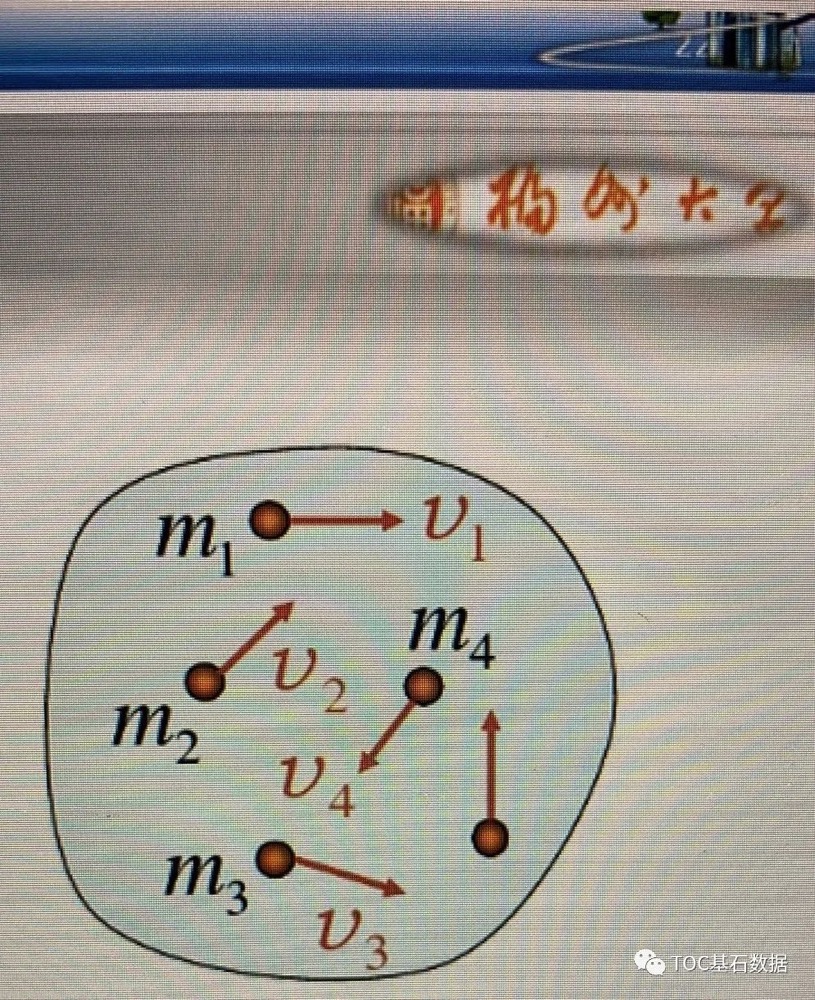
TOC理论认为所有平衡系统里面都存在一个瓶颈,在生产制造领域越长流程瓶颈制约条件越明显。
TOC理论认为系统的有效产出取决于系统瓶颈点的产出MV瓶颈≥MV入库,所以瓶颈点是系统的关键点,应用FαT=Mv的理论,将F作用在瓶颈这个关键点,有助于FαT的增加,从而将Mv的值变大,其中M=nm(不同多种产品),v是流速,从而增加产出。
在广义动量定理中的α取值范围在(-1,1)之间,但在TOC理论在解决系统问题可以取值在(0<α≤1)。
03|解决瓶颈的最有效办法
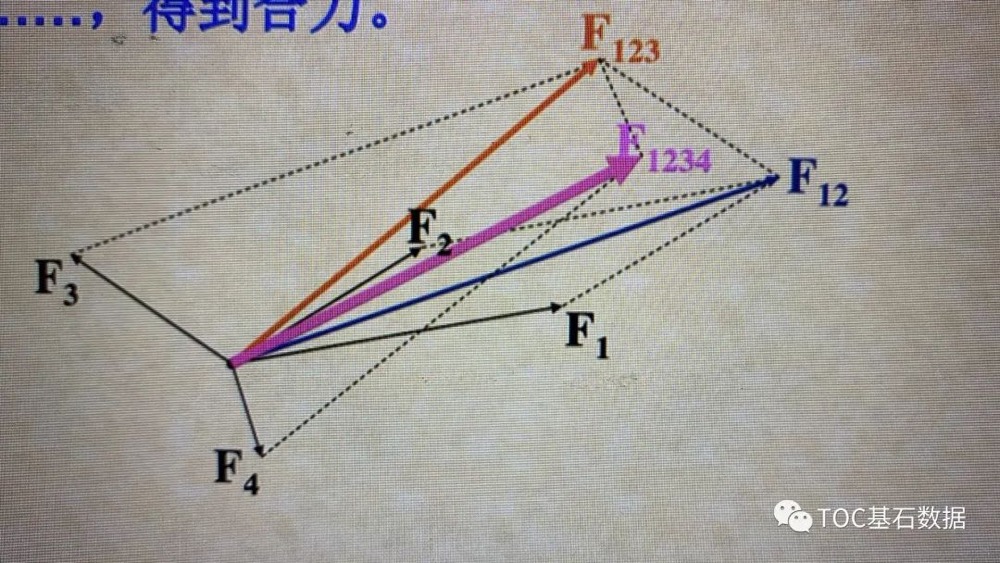
如何让我们的合力F和α的乘积最大化,是我们解决瓶颈的最有效办法,这些系统都是在原有平衡不变的情况下改变Fα变为最大值是我们工厂改变的根本,确切的说就是让所有不同的作用力合成一个正向并且推动系统正向流的合力,而不是所有作用力相互抵消及内耗,等式的右边Mv广义的质量和广义的速度,其中M可以看成不同产品类型或不同产品数量的总和,理解为M=nm,这个广义质量在客户下订单时候是既定好的,所以Mv的变大,最终由v的改变来实现,v的改变是在不借助系统外的力量来完成的话就必须由Fα来实现,而不是增加T的·时间来实现,那么如何实现Fα的增量才是我们解决系统瓶颈的根本。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
神经网络理论研究的物理学思想介绍2025-01-16 1396
-
基石数据:TOC理论物理学浅析—MES和计划(十三)2023-11-13 1109
-
基石数据:TOC理论物理学浅析—日结日清(九)2023-11-09 1020
-
基石数据:TOC理论物理学浅析—列队生产(八)2023-11-07 879
-
基石数据:TOC理论物理学浅析—结存篇下(四)2023-11-02 1079
-
基石数据:TOC理论物理学浅析(二)2023-10-31 1042
-
“推翻”爱因斯坦理论,2022诺贝尔物理学奖大揭秘!2022-11-10 2909
-
新的热力学:量子物理学如何改变规则2022-08-10 1654
-
简述物理学的工具和对象2021-05-11 3619
-
人工智能的发展对天体物理学会有什么影响2019-12-10 2033
-
物理学两大基石的矛盾2019-03-12 4616
-
物理学2008-09-16 2119
全部0条评论

快来发表一下你的评论吧 !

